Structural identifiability

Last updated February 21, 2024

In the area of system identification, a dynamical system is structurally identifiable if it is possible to infer its unknown parameters by measuring its output over time. This problem arises in many branch of applied mathematics, since dynamical systems (such as the ones described by ordinary differential equations) are commonly utilized to model physical processes and these models contain unknown parameters that are typically estimated using experimental data.^[1]^[2]^[3]

However, in certain cases, the model structure may not permit a unique solution for this estimation problem, even when the data is continuous and free from noise. To avoid potential issues, it is recommended to verify the uniqueness of the solution in advance, prior to conducting any actual experiments. The lack of structural identifiability implies that there are multiple solutions for the problem of system identification, and the impossibility of distinguishing between these solutions suggests that the system has poor forecasting power as a model.^[4] On the other hand, control systems have been proposed with the goal of rendering the closed-loop system unidentifiable, decreasing its susceptibility to covert attacks targeting cyber-physical systems.^[5]

Examples

Linear time-invariant system

Source^[2]

Consider a linear time-invariant system with the following state-space representation:

${\begin{aligned}{\dot {x}}_{1}(t)&=-\theta _{1}x_{1},\\{\dot {x}}_{2}(t)&=\theta _{1}x_{1},\\y(t)&=\theta _{2}x_{2},\end{aligned}}$

and with initial conditions given by $x_{1}(0)=\theta _{3}$ and $x_{2}(0)=0$ . The solution of the output $y$ is

$y(t)=\theta _{2}\theta _{3}e^{-\theta _{1}t}\left(e^{\theta _{1}t}-1\right),$

which implies that the parameters $\theta _{2}$ and $\theta _{3}$ are not structurally identifiable. For instance, the parameters $\theta _{1}=1,\theta _{2}=1,\theta _{3}=1$ generates the same output as the parameters $\theta _{1}=1,\theta _{2}=2,\theta _{3}=0.5$ .

Non-linear system

Source^[3]

A model of a possible glucose homeostasis mechanism is given by the differential equations^[6]

${\begin{aligned}&{\dot {G}}=u(0)+u-(c+s_{\mathrm {i} }\,I)G,\\&{\dot {\beta }}=\beta \left({\frac {1.4583\cdot 10^{-5}}{1+\left({\frac {8.4}{G}}\right)^{1.7}}}-{\frac {1.7361\cdot 10^{-5}}{1+\left({\frac {G}{8.4}}\right)^{8.5}}}\right),\\&{\dot {I}}=p\,\beta \,{\frac {G^{2}}{\alpha ^{2}+G^{2}}}-\gamma \,I,\end{aligned}}$

where (c, s_i, p, α, γ) are parameters of the system, and the states are the plasma glucose concentration G, the plasma insulin concentration I, and the beta-cell functional mass β. It is possible to show that the parameters p and s_i are not structurally identifiable: any numerical choice of parameters p and s_i that have the same product ps_i are indistinguishable.^[3]

Practical identifiability

Structural identifiability is assessed by analyzing the dynamical equations of the system, and does not take into account possible noises in the measurement of the output. In contrast, practical non-identifiability also takes noises into account.^[1]^[7]

Other related notions

The notion of structurally identifiable is closely related to observability, which refers to the capacity of inferring the state of the system by measuring the trajectories of the system output. It is also closely related to data informativity, which refers to the proper selection of inputs that enables the inference of the unknown parameters.^[8]^[9]

The (lack of) structural identifiability is also important in the context of dynamical compensation of physiological control systems. These systems should ensure a precise dynamical response despite variations in certain parameters.^[10]^[11] In other words, while in the field of systems identification, unidentifiability is considered a negative property, in the context of dynamical compensation, unidentifiability becomes a desirable property.^[11]

Identifiability also appears in the context of inverse optimal control. Here, one assumes that the data comes from a solution of an optimal control problem with unknown parameters in the objective function. Here, identifiability refers to the possibility of infering the parameters present in the objective function by using the measured data.^[12]

Software

There exist many software that can be used for analyzing the identifiability of a system, including non-linear systems:^[13]

PottersWheel: MATLAB toolbox that uses profile likelihood for structural and practical identifiability analysis.
Julia library for assessing structural parameter identifiability.^[14]
STRIKE-GOLDD: MATLAB toolbox for structural identifiability analysis.^[15]

Related Research Articles

Bayesian inference is a method of statistical inference in which Bayes' theorem is used to update the probability for a hypothesis as more evidence or information becomes available. Fundamentally, Bayesian inference uses prior knowledge, in the form of a prior distribution in order to estimate posterior probabilities. Bayesian inference is an important technique in statistics, and especially in mathematical statistics. Bayesian updating is particularly important in the dynamic analysis of a sequence of data. Bayesian inference has found application in a wide range of activities, including science, engineering, philosophy, medicine, sport, and law. In the philosophy of decision theory, Bayesian inference is closely related to subjective probability, often called "Bayesian probability".

A Bayesian network is a probabilistic graphical model that represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG). While it is one of several forms of causal notation, causal networks are special cases of Bayesian networks. Bayesian networks are ideal for taking an event that occurred and predicting the likelihood that any one of several possible known causes was the contributing factor. For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms. Given symptoms, the network can be used to compute the probabilities of the presence of various diseases.

In probability theory and statistics, the gamma distribution is a two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-squared distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use:

With a shape parameter $k$ and a scale parameter $θ$
With a shape parameter $and an inverse scale parameter, called a rate parameter.$

In statistics, the Rao–Blackwell theorem, sometimes referred to as the Rao–Blackwell–Kolmogorov theorem, is a result that characterizes the transformation of an arbitrarily crude estimator into an estimator that is optimal by the mean-squared-error criterion or any of a variety of similar criteria.

In mathematical statistics, the Fisher information is a way of measuring the amount of information that an observable random variable X carries about an unknown parameter θ of a distribution that models X. Formally, it is the variance of the score, or the expected value of the observed information.

Bayesian experimental design provides a general probability-theoretical framework from which other theories on experimental design can be derived. It is based on Bayesian inference to interpret the observations/data acquired during the experiment. This allows accounting for both any prior knowledge on the parameters to be determined as well as uncertainties in observations.

The Kuramoto model, first proposed by Yoshiki Kuramoto, is a mathematical model used in describing synchronization. More specifically, it is a model for the behavior of a large set of coupled oscillators. Its formulation was motivated by the behavior of systems of chemical and biological oscillators, and it has found widespread applications in areas such as neuroscience and oscillating flame dynamics. Kuramoto was quite surprised when the behavior of some physical systems, namely coupled arrays of Josephson junctions, followed his model.

The nested sampling algorithm is a computational approach to the Bayesian statistics problems of comparing models and generating samples from posterior distributions. It was developed in 2004 by physicist John Skilling.

Approximate Bayesian computation (ABC) constitutes a class of computational methods rooted in Bayesian statistics that can be used to estimate the posterior distributions of model parameters.

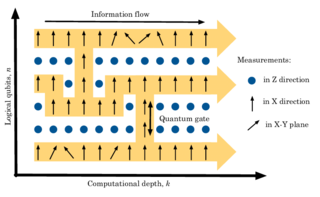
<span class="mw-page-title-main">One-way quantum computer</span> Method of quantum computing

The one-way or measurement-based quantum computer (MBQC) is a method of quantum computing that first prepares an entangled resource state, usually a cluster state or graph state, then performs single qubit measurements on it. It is "one-way" because the resource state is destroyed by the measurements.

In statistics, identifiability is a property which a model must satisfy for precise inference to be possible. A model is identifiable if it is theoretically possible to learn the true values of this model's underlying parameters after obtaining an infinite number of observations from it. Mathematically, this is equivalent to saying that different values of the parameters must generate different probability distributions of the observable variables. Usually the model is identifiable only under certain technical restrictions, in which case the set of these requirements is called the identification conditions.

The kicked rotator, also spelled as kicked rotor, is a paradigmatic model for both Hamiltonian chaos and quantum chaos. It describes a free rotating stick in an inhomogeneous "gravitation like" field that is periodically switched on in short pulses. The model is described by the Hamiltonian

Exponential Random Graph Models (ERGMs) are a family of statistical models for analyzing data from social and other networks. Examples of networks examined using ERGM include knowledge networks, organizational networks, colleague networks, social media networks, networks of scientific development, and others.

Iterated filtering algorithms are a tool for maximum likelihood inference on partially observed dynamical systems. Stochastic perturbations to the unknown parameters are used to explore the parameter space. Applying sequential Monte Carlo to this extended model results in the selection of the parameter values that are more consistent with the data. Appropriately constructed procedures, iterating with successively diminished perturbations, converge to the maximum likelihood estimate. Iterated filtering methods have so far been used most extensively to study infectious disease transmission dynamics. Case studies include cholera, Ebola virus, influenza, malaria, HIV, pertussis, poliovirus and measles. Other areas which have been proposed to be suitable for these methods include ecological dynamics and finance.

Linear optical quantum computing or linear optics quantum computation (LOQC), also photonic quantum computing (PQC), is a paradigm of quantum computation, allowing (under certain conditions, described below) universal quantum computation. LOQC uses photons as information carriers, mainly uses linear optical elements, or optical instruments (including reciprocal mirrors and waveplates) to process quantum information, and uses photon detectors and quantum memories to detect and store quantum information.

In machine learning, the vanishing gradient problem is encountered when training recurrent neural networks with gradient-based learning methods and backpropagation. In such methods, during each iteration of training each of the neural networks weights receives an update proportional to the partial derivative of the error function with respect to the current weight. The problem is that as the sequence length increases, the gradient magnitude typically is expected to decrease, slowing the training process. In the worst case, this may completely stop the neural network from further training. As one example of the problem cause, traditional activation functions such as the hyperbolic tangent function have gradients in the range $[-1,1]$ , and backpropagation computes gradients by the chain rule. This has the effect of multiplying $n$ of these small numbers to compute gradients of the early layers in an $n$ -layer network, meaning that the gradient decreases exponentially with $n$ while the early layers train very slowly.

The quantum Fisher information is a central quantity in quantum metrology and is the quantum analogue of the classical Fisher information. The quantum Fisher information $of a state with respect to the observable is defined as$

An energy-based model (EBM) (Canonical Ensemble Learning(CEL) or Learning via Canonical Ensemble (LCE)) is an application of canonical ensemble formulation of statistical physics for learning from data problems. Approach prominently appears in generative models.

Quantum artificial life is the application of quantum algorithms with the ability to simulate biological behavior. Quantum computers offer many potential improvements to processes performed on classical computers including machine learning and artificial intelligence. Artificial intelligence applications are often inspired by the idea of mimicking human brains; closely related biomimicry. This has been implemented to a certain extent on classical computers, but quantum computers offer many advantages in the simulation of artificial life. Artificial life and artificial intelligence are extremely similar with a minor differences; the goal of studying artificial life is to understand living beings better, while the goal of artificial intelligence is to create intelligent beings.

In quantum computing, the variational quantum eigensolver (VQE) is a quantum algorithm for quantum chemistry, quantum simulations and optimization problems. It is a hybrid algorithm that uses both classical computers and quantum computers to find the ground state of a given physical system. Given a guess or ansatz, the quantum processor calculates the expectation value of the system with respect to an observable, often the Hamiltonian, and a classical optimizer is used to improve the guess. The algorithm is based on the variational method of quantum mechanics.

References

1 2 Miao, Hongyu; Xia, Xiaohua; Perelson, Alan S.; Wu, Hulin (2011). "On Identifiability of Nonlinear ODE Models and Applications in Viral Dynamics". SIAM Review. 53 (1): 3–39. doi:10.1137/090757009. ISSN 0036-1445. PMC 3140286 . PMID 21785515. (Erratum: doi:10.1137/23M1568958)
1 2 Raue, A.; Karlsson, J.; Saccomani, M. P.; Jirstrand, M.; Timmer, J. (2014-05-15). "Comparison of approaches for parameter identifiability analysis of biological systems". Bioinformatics. 30 (10): 1440–1448. doi: 10.1093/bioinformatics/btu006 . ISSN 1367-4803. PMID 24463185. S2CID 10052322.
1 2 3 Villaverde, Alejandro F. (2019-01-01). "Observability and Structural Identifiability of Nonlinear Biological Systems". Complexity. 2019: 1–12. arXiv: 1812.04525 . doi: 10.1155/2019/8497093 . ISSN 1076-2787.
↑ Fiacchini, Mirko; Alamir, Mazen (2021). "The Ockham's razor applied to COVID-19 model fitting French data". Annual Reviews in Control. 51: 500–510. doi:10.1016/j.arcontrol.2021.01.002. PMC 7846253 . PMID 33551664.
↑ Mao, Xiangyu; He, Jianping (2023). "Unidentifiability of System Dynamics: Conditions and Controller Design". arXiv: 2308.15493 [eess.SY].
↑ Karin, Omer; Swisa, Avital; Glaser, Benjamin; Dor, Yuval; Alon, Uri (2016). "Dynamical compensation in physiological circuits". Molecular Systems Biology. 12 (11): 886. doi:10.15252/msb.20167216. ISSN 1744-4292. PMC 5147051 . PMID 27875241.
↑ Raue, A.; Kreutz, C.; Maiwald, T.; Bachmann, J.; Schilling, M.; Klingmüller, U.; Timmer, J. (2009-08-01). "Structural and practical identifiability analysis of partially observed dynamical models by exploiting the profile likelihood". Bioinformatics. 25 (15): 1923–1929. doi: 10.1093/bioinformatics/btp358 . ISSN 1460-2059. PMID 19505944.
↑ Van Waarde, Henk J.; Eising, Jaap; Camlibel, M. Kanat; Trentelman, Harry L. (2023). "The Informativity Approach: To Data-Driven Analysis and Control". IEEE Control Systems. 43 (6): 32–66. arXiv: 2302.10488 . doi:10.1109/MCS.2023.3310305. ISSN 1066-033X. S2CID 257050367.
↑ Gevers, Michel; Bazanella, Alexandre S.; Coutinho, Daniel F.; Dasgupta, Soura (2013). "Identifiability and excitation of polynomial systems". 52nd IEEE Conference on Decision and Control. Firenze: IEEE. pp. 4278–4283. doi:10.1109/CDC.2013.6760547. ISBN 978-1-4673-5717-3. S2CID 7796419.
↑ Karin, Omer; Swisa, Avital; Glaser, Benjamin; Dor, Yuval; Alon, Uri (2016). "Dynamical compensation in physiological circuits". Molecular Systems Biology. 12 (11): 886. doi:10.15252/msb.20167216. ISSN 1744-4292. PMC 5147051 . PMID 27875241.
1 2 Sontag, Eduardo D. (2017-04-06). Komarova, Natalia L. (ed.). "Dynamic compensation, parameter identifiability, and equivariances". PLOS Computational Biology. 13 (4): e1005447. Bibcode:2017PLSCB..13E5447S. doi: 10.1371/journal.pcbi.1005447 . ISSN 1553-7358. PMC 5398758 . PMID 28384175.
↑ Zhang, Han; Ringh, Axel (2024). "Inverse optimal control for averaged cost per stage linear quadratic regulators". Systems & Control Letters. 183: 105658. arXiv: 2305.15332 . doi:10.1016/j.sysconle.2023.105658.
↑ Barreiro, Xabier Rey; Villaverde, Alejandro F. (2023-01-31). "Benchmarking tools for a priori identifiability analysis". Bioinformatics. 39 (2): btad065. doi:10.1093/bioinformatics/btad065. ISSN 1367-4811. PMC 9913045 . PMID 36721336.
↑ Dong, Ruiwen; Goodbrake, Christian; Harrington, Heather A.; Pogudin, Gleb (2023-03-31). "Differential Elimination for Dynamical Models via Projections with Applications to Structural Identifiability". SIAM Journal on Applied Algebra and Geometry. 7 (1): 194–235. arXiv: 2111.00991 . doi:10.1137/22M1469067. ISSN 2470-6566. S2CID 245650629.
↑ Díaz-Seoane, Sandra; Rey-Barreiro, Xabier; Villaverde, Alejandro F. (2022-07-15). "STRIKE-GOLDD 4.0: user-friendly, efficient analysis of structural identifiability and observability". arXiv: 2207.07346 [eess.SY].

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[:0-1] 1 2 Miao, Hongyu; Xia, Xiaohua; Perelson, Alan S.; Wu, Hulin (2011). "On Identifiability of Nonlinear ODE Models and Applications in Viral Dynamics". SIAM Review. 53 (1): 3–39. doi:10.1137/090757009. ISSN 0036-1445. PMC 3140286 . PMID 21785515. (Erratum: doi:10.1137/23M1568958)

[:3-2] 1 2 Raue, A.; Karlsson, J.; Saccomani, M. P.; Jirstrand, M.; Timmer, J. (2014-05-15). "Comparison of approaches for parameter identifiability analysis of biological systems". Bioinformatics. 30 (10): 1440–1448. doi: 10.1093/bioinformatics/btu006 . ISSN 1367-4803. PMID 24463185. S2CID 10052322.

[:2-3] 1 2 3 Villaverde, Alejandro F. (2019-01-01). "Observability and Structural Identifiability of Nonlinear Biological Systems". Complexity. 2019: 1–12. arXiv: 1812.04525 . doi: 10.1155/2019/8497093 . ISSN 1076-2787.

[:1-4] Fiacchini, Mirko; Alamir, Mazen (2021). "The Ockham's razor applied to COVID-19 model fitting French data". Annual Reviews in Control. 51: 500–510. doi:10.1016/j.arcontrol.2021.01.002. PMC 7846253 . PMID 33551664.

[5] Mao, Xiangyu; He, Jianping (2023). "Unidentifiability of System Dynamics: Conditions and Controller Design". arXiv: 2308.15493 [eess.SY].

[6] Karin, Omer; Swisa, Avital; Glaser, Benjamin; Dor, Yuval; Alon, Uri (2016). "Dynamical compensation in physiological circuits". Molecular Systems Biology. 12 (11): 886. doi:10.15252/msb.20167216. ISSN 1744-4292. PMC 5147051 . PMID 27875241.

[7] Raue, A.; Kreutz, C.; Maiwald, T.; Bachmann, J.; Schilling, M.; Klingmüller, U.; Timmer, J. (2009-08-01). "Structural and practical identifiability analysis of partially observed dynamical models by exploiting the profile likelihood". Bioinformatics. 25 (15): 1923–1929. doi: 10.1093/bioinformatics/btp358 . ISSN 1460-2059. PMID 19505944.

[8] Van Waarde, Henk J.; Eising, Jaap; Camlibel, M. Kanat; Trentelman, Harry L. (2023). "The Informativity Approach: To Data-Driven Analysis and Control". IEEE Control Systems. 43 (6): 32–66. arXiv: 2302.10488 . doi:10.1109/MCS.2023.3310305. ISSN 1066-033X. S2CID 257050367.

[9] Gevers, Michel; Bazanella, Alexandre S.; Coutinho, Daniel F.; Dasgupta, Soura (2013). "Identifiability and excitation of polynomial systems". 52nd IEEE Conference on Decision and Control. Firenze: IEEE. pp. 4278–4283. doi:10.1109/CDC.2013.6760547. ISBN 978-1-4673-5717-3. S2CID 7796419.

[10] Karin, Omer; Swisa, Avital; Glaser, Benjamin; Dor, Yuval; Alon, Uri (2016). "Dynamical compensation in physiological circuits". Molecular Systems Biology. 12 (11): 886. doi:10.15252/msb.20167216. ISSN 1744-4292. PMC 5147051 . PMID 27875241.

[:4-11] 1 2 Sontag, Eduardo D. (2017-04-06). Komarova, Natalia L. (ed.). "Dynamic compensation, parameter identifiability, and equivariances". PLOS Computational Biology. 13 (4): e1005447. Bibcode:2017PLSCB..13E5447S. doi: 10.1371/journal.pcbi.1005447 . ISSN 1553-7358. PMC 5398758 . PMID 28384175.

[12] Zhang, Han; Ringh, Axel (2024). "Inverse optimal control for averaged cost per stage linear quadratic regulators". Systems & Control Letters. 183: 105658. arXiv: 2305.15332 . doi:10.1016/j.sysconle.2023.105658.

[13] Barreiro, Xabier Rey; Villaverde, Alejandro F. (2023-01-31). "Benchmarking tools for a priori identifiability analysis". Bioinformatics. 39 (2): btad065. doi:10.1093/bioinformatics/btad065. ISSN 1367-4811. PMC 9913045 . PMID 36721336.

[14] Dong, Ruiwen; Goodbrake, Christian; Harrington, Heather A.; Pogudin, Gleb (2023-03-31). "Differential Elimination for Dynamical Models via Projections with Applications to Structural Identifiability". SIAM Journal on Applied Algebra and Geometry. 7 (1): 194–235. arXiv: 2111.00991 . doi:10.1137/22M1469067. ISSN 2470-6566. S2CID 245650629.

[15] Díaz-Seoane, Sandra; Rey-Barreiro, Xabier; Villaverde, Alejandro F. (2022-07-15). "STRIKE-GOLDD 4.0: user-friendly, efficient analysis of structural identifiability and observability". arXiv: 2207.07346 [eess.SY].

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]