
The Huygens–Fresnel principle states that every point on a wavefront is itself the source of spherical wavelets, and the secondary wavelets emanating from different points mutually interfere. The sum of these spherical wavelets forms a new wavefront. As such, the Huygens-Fresnel principle is a method of analysis applied to problems of luminous wave propagation both in the far-field limit and in near-field diffraction as well as reflection.

A waveguide is a structure that guides waves by restricting the transmission of energy to one direction. Common types of waveguides include acoustic waveguides which direct sound, optical waveguides which direct light, and radio-frequency waveguides which direct electromagnetic waves other than light like radio waves.
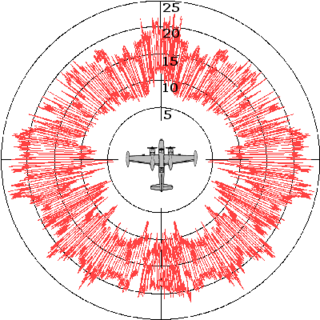
Radar cross-section (RCS), denoted σ, also called radar signature, is a measure of how detectable an object is by radar. A larger RCS indicates that an object is more easily detected.

A metamaterial is any material engineered to have a property that is rarely observed in naturally occurring materials. They are made from assemblies of multiple elements fashioned from composite materials such as metals and plastics. These materials are usually arranged in repeating patterns, at scales that are smaller than the wavelengths of the phenomena they influence. Metamaterials derive their properties not from the properties of the base materials, but from their newly designed structures. Their precise shape, geometry, size, orientation and arrangement gives them their smart properties capable of manipulating electromagnetic waves: by blocking, absorbing, enhancing, or bending waves, to achieve benefits that go beyond what is possible with conventional materials.

Finite-difference time-domain (FDTD) or Yee's method is a numerical analysis technique used for modeling computational electrodynamics. Since it is a time-domain method, FDTD solutions can cover a wide frequency range with a single simulation run, and treat nonlinear material properties in a natural way.
The electric-field integral equation is a relationship that allows the calculation of an electric field generated by an electric current distribution.

In classical electromagnetism, reciprocity refers to a variety of related theorems involving the interchange of time-harmonic electric current densities (sources) and the resulting electromagnetic fields in Maxwell's equations for time-invariant linear media under certain constraints. Reciprocity is closely related to the concept of symmetric operators from linear algebra, applied to electromagnetism.

In physics, physical optics, or wave optics, is the branch of optics that studies interference, diffraction, polarization, and other phenomena for which the ray approximation of geometric optics is not valid. This usage tends not to include effects such as quantum noise in optical communication, which is studied in the sub-branch of coherence theory.

Computational electromagnetics (CEM), computational electrodynamics or electromagnetic modeling is the process of modeling the interaction of electromagnetic fields with physical objects and the environment using computers.

Constantine A. Balanis is a Greek-born American scientist, educator, author, and Regents Professor at Arizona State University. Born in Trikala, Greece on October 29, 1938. He is best known for his books in the fields of engineering electromagnetics and antenna theory. He emigrated to the United States in 1955, where he studied electrical engineering. He received United States citizenship in 1960.
Characteristic modes (CM) form a set of functions which, under specific boundary conditions, diagonalizes operator relating field and induced sources. Under certain conditions, the set of the CM is unique and complete (at least theoretically) and thereby capable of describing the behavior of a studied object in full.

A substrate-integrated waveguide (SIW) is a synthetic rectangular electromagnetic waveguide formed in a dielectric substrate by densely arraying metallized posts or via holes that connect the upper and lower metal plates of the substrate. The waveguide can be easily fabricated with low-cost mass-production using through-hole techniques, where the post walls consists of via fences. SIW is known to have similar guided wave and mode characteristics to conventional rectangular waveguide with equivalent guide wavelength.

The history of metamaterials begins with artificial dielectrics in microwave engineering as it developed just after World War II. Yet, there are seminal explorations of artificial materials for manipulating electromagnetic waves at the end of the 19th century. Hence, the history of metamaterials is essentially a history of developing certain types of manufactured materials, which interact at radio frequency, microwave, and later optical frequencies.
Dr. Raymond J. Luebbers was Professor of Electrical Engineering at The Pennsylvania State University and Ohio University, a Research Scientist at the Lockheed Martin Research Laboratory in Palo Alto, CA and founder of Remcom, Inc.
The total active reflection coefficient (TARC) within mathematics and physics scattering theory, relates the total incident power to the total outgoing power in an N-port microwave component. The TARC is mainly used for multiple-input multiple-output (MIMO) antenna systems and array antennas, where the outgoing power is unwanted reflected power. The name shows the similarities with the active reflection coefficient, which is used for single elements. The TARC is the square root of the sum of all outgoing powers at the ports, divided by the sum of all incident powers at the ports of an N-port antenna. Similarly to the active reflection coefficient, the TARC is a function of frequency, and it also depends on scan angle and tapering. With this definition we can characterize the multi-port antenna’s frequency bandwidth and radiation performance. When the antennas are made of lossless materials, TARC can be computed directly from the scattering matrix by
Ulrich Jakobus is Senior Vice President - Electromagnetic Solutions of Altair, Germany and was awarded Fellow of the Institute of Electrical and Electronics Engineers (IEEE) in 2013 for leadership in hybrid computational tool development and commercialization. His research laid the foundations for the commercial electromagnetics code FEKO which is used in antenna design, antenna placement, electromagnetic compatibility, microwave components, bioelectromagnetics, radar cross section and related fields.

Weng Cho Chew is a Malaysian-American electrical engineer and applied physicist known for contributions to wave physics, especially computational electromagnetics. He is a Distinguished Professor of Electrical and Computer Engineering at Purdue University.
Roger Fuller Harrington is an American electrical engineer and professor emeritus at Syracuse University. He is best known for his contributions to computational electromagnetics with his development of method of moments (MoM). Harrington's 1968 book, Field Computation by Moment Methods, is regarded as a pivotal textbook on the subject.

The method of moments (MoM), also known as the moment method and method of weighted residuals, is a numerical method in computational electromagnetics. It is used in computer programs that simulate the interaction of electromagnetic fields such as radio waves with matter, for example antenna simulation programs like NEC that calculate the radiation pattern of an antenna. Generally being a frequency-domain method, it involves the projection of an integral equation into a system of linear equations by the application of appropriate boundary conditions. This is done by using discrete meshes as in finite difference and finite element methods, often for the surface. The solutions are represented with the linear combination of pre-defined basis functions; generally, the coefficients of these basis functions are the sought unknowns. Green's functions and Galerkin method play a central role in the method of moments.




























