Convection is single or multiphase fluid flow that occurs spontaneously due to the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity. When the cause of the convection is unspecified, convection due to the effects of thermal expansion and buoyancy can be assumed. Convection may also take place in soft solids or mixtures where particles can flow.
Boiling or ebullition is the rapid phase transition from liquid to gas or vapour; the reverse of boiling is condensation. Boiling occurs when a liquid is heated to its boiling point, so that the vapour pressure of the liquid is equal to the pressure exerted on the liquid by the surrounding atmosphere. Boiling and evaporation are the two main forms of liquid vapourization.
In thermal fluid dynamics, the Nusselt number is the ratio of total heat transfer to conductive heat transfer at a boundary in a fluid. Total heat transfer combines conduction and convection. Convection includes both advection and diffusion (conduction). The conductive component is measured under the same conditions as the convective but for a hypothetically motionless fluid. It is a dimensionless number, closely related to the fluid's Rayleigh number.
In the study of heat transfer, Newton's law of cooling is a physical law which states that the rate of heat loss of a body is directly proportional to the difference in the temperatures between the body and its environment. The law is frequently qualified to include the condition that the temperature difference is small and the nature of heat transfer mechanism remains the same. As such, it is equivalent to a statement that the heat transfer coefficient, which mediates between heat losses and temperature differences, is a constant.
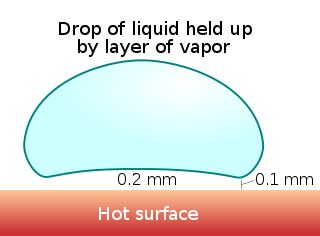
The Leidenfrost effect is a physical phenomenon in which a liquid, close to a solid surface of another body that is significantly hotter than the liquid's boiling point, produces an insulating vapor layer that keeps the liquid from boiling rapidly. Because of this repulsive force, a droplet hovers over the surface, rather than making physical contact with it. The effect is named after the German doctor Johann Gottlob Leidenfrost, who described it in A Tract About Some Qualities of Common Water.
A boiling water reactor (BWR) is a type of light water nuclear reactor used for the generation of electrical power. It is the second most common type of electricity-generating nuclear reactor after the pressurized water reactor (PWR), which is also a type of light water nuclear reactor.
Heat transfer is a discipline of thermal engineering that concerns the generation, use, conversion, and exchange of thermal energy (heat) between physical systems. Heat transfer is classified into various mechanisms, such as thermal conduction, thermal convection, thermal radiation, and transfer of energy by phase changes. Engineers also consider the transfer of mass of differing chemical species, either cold or hot, to achieve heat transfer. While these mechanisms have distinct characteristics, they often occur simultaneously in the same system.
A heat pipe is a heat-transfer device that employs phase transition to transfer heat between two solid interfaces.
In thermodynamics, the heat transfer coefficient or film coefficient, or film effectiveness, is the proportionality constant between the heat flux and the thermodynamic driving force for the flow of heat. It is used in calculating the heat transfer, typically by convection or phase transition between a fluid and a solid. The heat transfer coefficient has SI units in watts per square meter per kelvin (W/m2K).
A coolant is a substance, typically liquid, that is used to reduce or regulate the temperature of a system. An ideal coolant has high thermal capacity, low viscosity, is low-cost, non-toxic, chemically inert and neither causes nor promotes corrosion of the cooling system. Some applications also require the coolant to be an electrical insulator.
The supercritical water reactor (SCWR) is a concept Generation IV reactor, designed as a light water reactor (LWR) that operates at supercritical pressure. The term critical in this context refers to the critical point of water, and should not be confused with the concept of criticality of the nuclear reactor.
A zeotropicmixture, or non-azeotropic mixture, is a mixture with liquid components that have different boiling points. For example, nitrogen, methane, ethane, propane, and isobutane constitute a zeotropic mixture. Individual substances within the mixture do not evaporate or condense at the same temperature as one substance. In other words, the mixture has a temperature glide, as the phase change occurs in a temperature range of about four to seven degrees Celsius, rather than at a constant temperature. On temperature-composition graphs, this temperature glide can be seen as the temperature difference between the bubble point and dew point. For zeotropic mixtures, the temperatures on the bubble (boiling) curve are between the individual component's boiling temperatures. When a zeotropic mixture is boiled or condensed, the composition of the liquid and the vapor changes according to the mixtures's temperature-composition diagram.
In the study of heat transfer, critical heat flux (CHF) is the heat flux at which boiling ceases to be an effective form of transferring heat from a solid surface to a liquid.
A reaction calorimeter is a calorimeter that measures the amount of energy released or absorbed by a chemical reaction. It does this by measuring the total change in temperature of an exact amount of water in a vessel.
Micro heat exchangers,Micro-scale heat exchangers, or microstructured heat exchangers are heat exchangers in which fluid flows in lateral confinements with typical dimensions below 1 mm. The most typical such confinement are microchannels, which are channels with a hydraulic diameter below 1 mm. Microchannel heat exchangers can be made from metal or ceramic.
In fluid thermodynamics, nucleate boiling is a type of boiling that takes place when the surface temperature is hotter than the saturated fluid temperature by a certain amount but where the heat flux is below the critical heat flux. For water, as shown in the graph below, nucleate boiling occurs when the surface temperature is higher than the saturation temperature by between 10 and 30 °C. The critical heat flux is the peak on the curve between nucleate boiling and transition boiling. The heat transfer from surface to liquid is greater than that in film boiling.
In engineering, physics, and chemistry, the study of transport phenomena concerns the exchange of mass, energy, charge, momentum and angular momentum between observed and studied systems. While it draws from fields as diverse as continuum mechanics and thermodynamics, it places a heavy emphasis on the commonalities between the topics covered. Mass, momentum, and heat transport all share a very similar mathematical framework, and the parallels between them are exploited in the study of transport phenomena to draw deep mathematical connections that often provide very useful tools in the analysis of one field that are directly derived from the others.
In fluid dynamics, the entrance length is the distance a flow travels after entering a pipe before the flow becomes fully developed. Entrance length refers to the length of the entry region, the area following the pipe entrance where effects originating from the interior wall of the pipe propagate into the flow as an expanding boundary layer. When the boundary layer expands to fill the entire pipe, the developing flow becomes a fully developed flow, where flow characteristics no longer change with increased distance along the pipe. Many different entrance lengths exist to describe a variety of flow conditions. Hydrodynamic entrance length describes the formation of a velocity profile caused by viscous forces propagating from the pipe wall. Thermal entrance length describes the formation of a temperature profile. Awareness of entrance length may be necessary for the effective placement of instrumentation, such as fluid flow meters.
Heat transfer enhancement is the process of increasing the effectiveness of heat exchangers. This can be achieved when the heat transfer power of a given device is increased or when the pressure losses generated by the device are reduced. A variety of techniques can be applied to this effect, including generating strong secondary flows or increasing boundary layer turbulence.
The removal of heat from nuclear reactors is an essential step in the generation of energy from nuclear reactions. In nuclear engineering there are a number of empirical or semi-empirical relations used for quantifying the process of removing heat from a nuclear reactor core so that the reactor operates in the projected temperature interval that depends on the materials used in the construction of the reactor. The effectiveness of removal of heat from the reactor core depends on many factors, including the cooling agents used and the type of reactor. Common liquid coolants for nuclear reactors include: deionized water, heavy water, the lighter alkaline metals, lead or lead-based eutectic alloys like lead-bismuth, and NaK, a eutectic alloy of sodium and potassium. Gas cooled reactors operate with coolants like carbon dioxide, helium or nitrogen but some very low powered research reactors have even been air-cooled with Chicago Pile 1 relying on natural convection of the surrounding air to remove the negligible thermal power output. There is ongoing research into using supercritical fluids as reactor coolants but thus far neither the supercritical water reactor nor a reactor cooled with supercritical Carbon Dioxide nor any other kind of supercritical-fluid-cooled reactor has ever been built.
