In quantum mechanics, a Hamiltonian is an operator corresponding to the sum of the kinetic energies plus the potential energies for all the particles in the system. It is usually denoted by , but also or to highlight its function as an operator. Its spectrum is the set of possible outcomes when one measures the total energy of a system. Because of its close relation to the time-evolution of a system, it is of fundamental importance in most formulations of quantum theory.
In quantum chemistry and molecular physics, the Born–Oppenheimer (BO) approximation is the assumption that the motion of atomic nuclei and electrons in a molecule can be treated separately. The approach is named after Max Born and J. Robert Oppenheimer who proposed it in 1927, in the early period of quantum mechanics. The approximation is widely used in quantum chemistry to speed up the computation of molecular wavefunctions and other properties for large molecules. There are cases where the assumption of separable motion no longer holds, which make the approximation lose validity, but is then often used as a starting point for more refined methods.
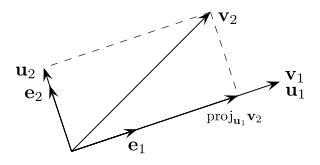
In mathematics, particularly linear algebra and numerical analysis, the Gram–Schmidt process is a method for orthonormalising a set of vectors in an inner product space, most commonly the Euclidean space Rn equipped with the standard inner product. The Gram–Schmidt process takes a finite, linearly independent set S = {v1, ..., vk} for k ≤ n and generates an orthogonal set S′ = {u1, ..., uk} that spans the same k-dimensional subspace of Rn as S.
In differential geometry, a (smooth) Riemannian manifold or (smooth) Riemannian space(M, g) is a real, smooth manifold M equipped with an inner product gp on the tangent space TpM at each point p that varies smoothly from point to point in the sense that if X and Y are differentiable vector fields on M, then p ↦ gp(X|p, Y|p) is a smooth function. The family gp of inner products is called a Riemannian metric. These terms are named after the German mathematician Bernhard Riemann. The study of Riemannian manifolds constitutes the subject called Riemannian geometry.
In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K(σp) depends on a two-dimensional plane σp in the tangent space at a point p of the manifold. It is the Gaussian curvature of the surface which has the plane σp as a tangent plane at p, obtained from geodesics which start at p in the directions of σp. The sectional curvature is a smooth real-valued function on the 2-Grassmannian bundle over the manifold.

In differential geometry, the Gaussian curvature or Gauss curvatureΚ of a surface at a point is the product of the principal curvatures, κ1 and κ2, at the given point:

In mathematics, specifically differential geometry, the infinitesimal geometry of Riemannian manifolds with dimension greater than 2 is too complicated to be described by a single number at a given point. Riemann introduced an abstract and rigorous way to define curvature for these manifolds, now known as the Riemann curvature tensor. Similar notions have found applications everywhere in differential geometry.
In linear algebra, the Gram matrix of a set of vectors in an inner product space is the Hermitian matrix of inner products, whose entries are given by .
In physics, the Clebsch–Gordan (CG) coefficients are numbers that arise in angular momentum coupling in quantum mechanics. They appear as the expansion coefficients of total angular momentum eigenstates in an uncoupled tensor product basis. In more mathematical terms, the CG coefficients are used in representation theory, particularly of compact Lie groups, to perform the explicit direct sum decomposition of the tensor product of two irreducible representations into irreducible representations, in cases where the numbers and types of irreducible components are already known abstractly. The name derives from the German mathematicians Alfred Clebsch and Paul Gordan, who encountered an equivalent problem in invariant theory.

In quantum field theory, the LSZ reduction formula is a method to calculate S-matrix elements from the time-ordered correlation functions of a quantum field theory. It is a step of the path that starts from the Lagrangian of some quantum field theory and leads to prediction of measurable quantities. It is named after the three German physicists Harry Lehmann, Kurt Symanzik and Wolfhart Zimmermann.
In differential geometry, the Laplace operator, named after Pierre-Simon Laplace, can be generalized to operate on functions defined on surfaces in Euclidean space and, more generally, on Riemannian and pseudo-Riemannian manifolds. This more general operator goes by the name Laplace–Beltrami operator, after Laplace and Eugenio Beltrami. Like the Laplacian, the Laplace–Beltrami operator is defined as the divergence of the gradient, and is a linear operator taking functions into functions. The operator can be extended to operate on tensors as the divergence of the covariant derivative. Alternatively, the operator can be generalized to operate on differential forms using the divergence and exterior derivative. The resulting operator is called the Laplace–de Rham operator.
In mathematics, the musical isomorphism is an isomorphism between the tangent bundle and the cotangent bundle of a pseudo-Riemannian manifold induced by its metric tensor. There are similar isomorphisms on symplectic manifolds. The term musical refers to the use of the symbols (flat) and (sharp). The exact origin of this notation is not known, but the term musicality in this context would be due to Marcel Berger.
In mathematics, a holomorphic vector bundle is a complex vector bundle over a complex manifold X such that the total space E is a complex manifold and the projection map π : E → X is holomorphic. Fundamental examples are the holomorphic tangent bundle of a complex manifold, and its dual, the holomorphic cotangent bundle. A holomorphic line bundle is a rank one holomorphic vector bundle.
In mathematics, in the field of functional analysis, an indefinite inner product space
Photon polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. An individual photon can be described as having right or left circular polarization, or a superposition of the two. Equivalently, a photon can be described as having horizontal or vertical linear polarization, or a superposition of the two.
In many-body theory, the term Green's function is sometimes used interchangeably with correlation function, but refers specifically to correlators of field operators or creation and annihilation operators.
In Riemannian geometry, the Gauss–Codazzi–Mainardi equations are fundamental equations in the theory of embedded hypersurfaces in a Euclidean space, and more generally submanifolds of Riemannian manifolds. They also have applications for embedded hypersurfaces of pseudo-Riemannian manifolds.
In pure and applied mathematics, quantum mechanics and computer graphics, a tensor operator generalizes the notion of operators which are scalars and vectors. A special class of these are spherical tensor operators which apply the notion of the spherical basis and spherical harmonics. The spherical basis closely relates to the description of angular momentum in quantum mechanics and spherical harmonic functions. The coordinate-free generalization of a tensor operator is known as a representation operator.







