In differential geometry, the second fundamental form (or shape tensor) is a quadratic form on the tangent plane of a smooth surface in the three-dimensional Euclidean space, usually denoted by (read "two"). Together with the first fundamental form, it serves to define extrinsic invariants of the surface, its principal curvatures. More generally, such a quadratic form is defined for a smooth immersed submanifold in a Riemannian manifold.
The second fundamental form of a parametric surface S in R3 was introduced and studied by Gauss. First suppose that the surface is the graph of a twice continuously differentiable function, z = f(x,y), and that the plane z = 0 is tangent to the surface at the origin. Then f and its partial derivatives with respect to x and y vanish at (0,0). Therefore, the Taylor expansion of f at (0,0) starts with quadratic terms:
and the second fundamental form at the origin in the coordinates (x,y) is the quadratic form
For a smooth point P on S, one can choose the coordinate system so that the plane z = 0 is tangent to S at P, and define the second fundamental form in the same way.
The second fundamental form of a general parametric surface is defined as follows. Let r = r(u,v) be a regular parametrization of a surface in R3, where r is a smooth vector-valued function of two variables. It is common to denote the partial derivatives of r with respect to u and v by ru and rv. Regularity of the parametrization means that ru and rv are linearly independent for any (u,v) in the domain of r, and hence span the tangent plane to S at each point. Equivalently, the cross product ru × rv is a nonzero vector normal to the surface. The parametrization thus defines a field of unit normal vectors n:
The second fundamental form is usually written as
its matrix in the basis {ru, rv} of the tangent plane is
The coefficients L, M, N at a given point in the parametric uv-plane are given by the projections of the second partial derivatives of r at that point onto the normal line to S and can be computed with the aid of the dot product as follows:
For a signed distance field of Hessian H, the second fundamental form coefficients can be computed as follows:
The second fundamental form of a general parametric surface S is defined as follows.
Let r = r(u1,u2) be a regular parametrization of a surface in R3, where r is a smooth vector-valued function of two variables. It is common to denote the partial derivatives of r with respect to uα by rα, α = 1, 2. Regularity of the parametrization means that r1 and r2 are linearly independent for any (u1,u2) in the domain of r, and hence span the tangent plane to S at each point. Equivalently, the cross product r1 × r2 is a nonzero vector normal to the surface. The parametrization thus defines a field of unit normal vectors n:
The second fundamental form is usually written as
The equation above uses the Einstein summation convention.
The coefficients bαβ at a given point in the parametric u1u2-plane are given by the projections of the second partial derivatives of r at that point onto the normal line to S and can be computed in terms of the normal vector n as follows:
In Euclidean space, the second fundamental form is given by
where is the Gauss map, and the differential of regarded as a vector-valued differential form, and the brackets denote the metric tensor of Euclidean space.
More generally, on a Riemannian manifold, the second fundamental form is an equivalent way to describe the shape operator (denoted by S) of a hypersurface,
where ∇vw denotes the covariant derivative of the ambient manifold and n a field of normal vectors on the hypersurface. (If the affine connection is torsion-free, then the second fundamental form is symmetric.)
The sign of the second fundamental form depends on the choice of direction of n (which is called a co-orientation of the hypersurface - for surfaces in Euclidean space, this is equivalently given by a choice of orientation of the surface).
The second fundamental form can be generalized to arbitrary codimension. In that case it is a quadratic form on the tangent space with values in the normal bundle and it can be defined by
where denotes the orthogonal projection of covariant derivative onto the normal bundle.
In Euclidean space, the curvature tensor of a submanifold can be described by the following formula:
This is called the Gauss equation , as it may be viewed as a generalization of Gauss's Theorema Egregium.
For general Riemannian manifolds one has to add the curvature of ambient space; if N is a manifold embedded in a Riemannian manifold (M,g) then the curvature tensor RN of N with induced metric can be expressed using the second fundamental form and RM, the curvature tensor of M:
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.
In vector calculus, the divergence theorem, also known as Gauss's theorem or Ostrogradsky's theorem, is a theorem which relates the flux of a vector field through a closed surface to the divergence of the field in the volume enclosed.
In geometry, a normal is an object that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the line perpendicular to the tangent line to the curve at the point.
In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K(σp) depends on a two-dimensional linear subspace σp of the tangent space at a point p of the manifold. It can be defined geometrically as the Gaussian curvature of the surface which has the plane σp as a tangent plane at p, obtained from geodesics which start at p in the directions of σp. The sectional curvature is a real-valued function on the 2-Grassmannian bundle over the manifold.
In differential geometry, the Gaussian curvature or Gauss curvatureΚ of a smooth surface in three-dimensional space at a point is the product of the principal curvatures, κ1 and κ2, at the given point:
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given by a principal connection on the frame bundle – see affine connection. In the special case of a manifold isometrically embedded into a higher-dimensional Euclidean space, the covariant derivative can be viewed as the orthogonal projection of the Euclidean directional derivative onto the manifold's tangent space. In this case the Euclidean derivative is broken into two parts, the extrinsic normal component and the intrinsic covariant derivative component.
Differential geometry of curves is the branch of geometry that deals with smooth curves in the plane and the Euclidean space by methods of differential and integral calculus.
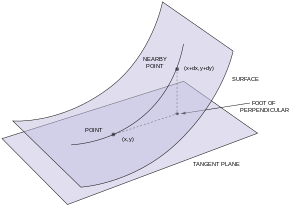
In differential geometry, the first fundamental form is the inner product on the tangent space of a surface in three-dimensional Euclidean space which is induced canonically from the dot product of R3. It permits the calculation of curvature and metric properties of a surface such as length and area in a manner consistent with the ambient space. The first fundamental form is denoted by the Roman numeral I,
In mathematics, particularly multivariable calculus, a surface integral is a generalization of multiple integrals to integration over surfaces. It can be thought of as the double integral analogue of the line integral. Given a surface, one may integrate over this surface a scalar field, or a vector field. If a region R is not flat, then it is called a surface as shown in the illustration.
In differential geometry, an affine connection is a geometric object on a smooth manifold which connects nearby tangent spaces, so it permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space. Connections are among the simplest methods of defining differentiation of the sections of vector bundles.
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections, the associated holonomy is a type of monodromy and is an inherently global notion. For curved connections, holonomy has nontrivial local and global features.
In mathematics, specifically differential geometry, the infinitesimal geometry of Riemannian manifolds with dimension greater than 2 is too complicated to be described by a single number at a given point. Riemann introduced an abstract and rigorous way to define curvature for these manifolds, now known as the Riemann curvature tensor. Similar notions have found applications everywhere in differential geometry of surfaces and other objects. The curvature of a pseudo-Riemannian manifold can be expressed in the same way with only slight modifications.
In differential geometry, the Frenet–Serret formulas describe the kinematic properties of a particle moving along a differentiable curve in three-dimensional Euclidean space , or the geometric properties of the curve itself irrespective of any motion. More specifically, the formulas describe the derivatives of the so-called tangent, normal, and binormal unit vectors in terms of each other. The formulas are named after the two French mathematicians who independently discovered them: Jean Frédéric Frenet, in his thesis of 1847, and Joseph Alfred Serret, in 1851. Vector notation and linear algebra currently used to write these formulas were not yet available at the time of their discovery.
A parametric surface is a surface in the Euclidean space which is defined by a parametric equation with two parameters . Parametric representation is a very general way to specify a surface, as well as implicit representation. Surfaces that occur in two of the main theorems of vector calculus, Stokes' theorem and the divergence theorem, are frequently given in a parametric form. The curvature and arc length of curves on the surface, surface area, differential geometric invariants such as the first and second fundamental forms, Gaussian, mean, and principal curvatures can all be computed from a given parametrization.
In differential geometry, the notion of torsion is a manner of characterizing a twist or screw of a moving frame around a curve. The torsion of a curve, as it appears in the Frenet–Serret formulas, for instance, quantifies the twist of a curve about its tangent vector as the curve evolves. In the geometry of surfaces, the geodesic torsion describes how a surface twists about a curve on the surface. The companion notion of curvature measures how moving frames "roll" along a curve "without twisting".
In mathematics, a holomorphic vector bundle is a complex vector bundle over a complex manifold X such that the total space E is a complex manifold and the projection map π : E → X is holomorphic. Fundamental examples are the holomorphic tangent bundle of a complex manifold, and its dual, the holomorphic cotangent bundle. A holomorphic line bundle is a rank one holomorphic vector bundle.
In Riemannian geometry and pseudo-Riemannian geometry, the Gauss–Codazzi equations are fundamental formulas which link together the induced metric and second fundamental form of a submanifold of a Riemannian or pseudo-Riemannian manifold.
In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth surfaces with various additional structures, most often, a Riemannian metric. Surfaces have been extensively studied from various perspectives: extrinsically, relating to their embedding in Euclidean space and intrinsically, reflecting their properties determined solely by the distance within the surface as measured along curves on the surface. One of the fundamental concepts investigated is the Gaussian curvature, first studied in depth by Carl Friedrich Gauss, who showed that curvature was an intrinsic property of a surface, independent of its isometric embedding in Euclidean space.
In differential geometry, the third fundamental form is a surface metric denoted by . Unlike the second fundamental form, it is independent of the surface normal.
In mathematics, hyperbolic complex space is a Hermitian manifold which is the equivalent of the real hyperbolic space in the context of complex manifolds. The complex hyperbolic space is a Kähler manifold, and it is characterised by being the only simply connected Kähler manifold whose holomorphic sectional curvature is constant equal to -1. Its underlying Riemannian manifold has non-constant negative curvature, pinched between -1 and -1/4 : in particular, it is a CAT(-1/4) space.
