Vertical deflection

Last updated
Earth's ellipsoid, geoid, and two types of vertical deflection GRAVIMETRIC DATUM ORIENTATION.SVG
Earth's ellipsoid, geoid, and two types of vertical deflection

The vertical deflection (VD) or deflection of the vertical (DoV), also known as deflection of the plumb line and astro-geodetic deflection, is a measure of how far the gravity direction at a given point of interest is rotated by local mass anomalies such as nearby mountains. They are widely used in geodesy, for surveying networks and for geophysical purposes.

Contents

The vertical deflection are the angular components between the true zenith–nadir curve (plumb line) tangent line and the normal vector to the surface of the reference ellipsoid (chosen to approximate the Earth's sea-level surface). VDs are caused by mountains and by underground geological irregularities and can amount to angles of 10″ in flat areas or 20–50″ in mountainous terrain).[ citation needed ]

The deflection of the vertical has a north–south component ξ (xi) and an east–west component η (eta). The value of ξ is the difference between the astronomic latitude and the geodetic latitude (taking north latitudes to be positive and south latitudes to be negative); the latter is usually calculated by geodetic network coordinates. The value of η is the product of cosine of latitude and the difference between the astronomic longitude and the longitude (taking east longitudes to be positive and west longitudes to be negative). When a new mapping datum replaces the old, with new geodetic latitudes and longitudes on a new ellipsoid, the calculated vertical deflections will also change.

Determination

The deflections reflect the undulation of the geoid and gravity anomalies, for they depend on the gravity field and its inhomogeneities.

Vertical deflections are usually determined astronomically. The true zenith is observed astronomically with respect to the stars, and the ellipsoidal zenith (theoretical vertical) by geodetic network computation, which always takes place on a reference ellipsoid. Additionally, the very local variations of the vertical deflection can be computed from gravimetric survey data and by means of digital terrain models (DTM), using a theory originally developed by Vening-Meinesz.

VDs are used in astrogeodetic levelling: as a vertical deflection describes the difference between the geoidal and ellipsoidal normal direction, it represents the horizontal spatial gradient of the geoid undulations of the geoid (i.e., the separation between geoid and reference ellipsoid).

In practice, the deflections are observed at special points with spacings of 20 or 50 kilometers. The densification is done by a combination of DTM models and areal gravimetry. Precise vertical deflection observations have accuracies of ±0.2″ (on high mountains ±0.5″), calculated values of about 1–2″.

The maximal vertical deflection of Central Europe seems to be a point near the Großglockner (3,798 m), the highest peak of the Austrian Alps. The approx. values are ξ = +50″ and η = −30″. In the Himalaya region, very asymmetric peaks may have vertical deflections up to 100″ (0.03°). In the rather flat area between Vienna and Hungary the values are less than 15", but scatter by ±10″ for irregular rock densities in the subsurface.

More recently, a combination of digital camera and tiltmeter have also been used, see zenith camera. [1]

Application

Vertical deflections are principally used in four matters:

  1. For precise calculation of survey networks. The geodetic theodolites and levelling instruments are oriented with respect to the true vertical, but its deflection exceeds the geodetic measuring accuracy by a factor of 5 to 50. Therefore, the data would have to be corrected exactly with respect to the global ellipsoid. Without these reductions, the surveys may be distorted by some centimeters or even decimeters per km.
  2. For the geoid determination (mean sea level) and for exact transformation of elevations. The global geoidal undulations amount to 50–100 m, and their regional values to 10–50 m. They are adequate to the integrals of VD components ξ,η and therefore can be calculated with cm accuracy over distances of many kilometers.
  3. For GPS surveys. The satellites measurements refer to a pure geometrical system (usually the WGS84 ellipsoid), whereas the terrestrial heights refer to the geoid. We need accurate geoid data to combine the different types of measurements.
  4. For geophysics . Because VD data are affected by the physical structure of the Earth's crust and mantle, geodesists are engaged in models to improve our knowledge of the Earth's interior. Additionally and similar to applied geophysics, the VD data can support the future exploration of raw materials, oil, gas or ores.

Historical implications

Vertical deflections were used to measure Earth's density in the Schiehallion experiment.

Vertical deflection is the reason why modern prime meridian passes more than 100 m to the east of the historical astronomic prime meridian in Greenwich. [2]

The meridian arc measurement made by Nicolas-Louis de Lacaille north of Cape Town in 1752 (de Lacaille's arc measurement) was affected by vertical deflection. [3] The resulting discrepancy with Northern Hemisphere measurements was not explained until a visit to the area by George Everest in 1820; Maclear's arc measurement resurvey ultimately confirmed Everest's conjecture. [4]

Errors in the meridian arc of Delambre and Méchain determination, which affected the original definition of the metre, [5] were long known to be mainly caused by an uncertain determination of Barcelona's latitude later explained by vertical deflection. [6] [7] [8] When these errors where acknowledged in 1866, [9] it became urgent to proceed to a new measurement of the French arc between Dunkirk and Perpignan. The operations concerning the revision of the French arc linked to Spanish triangulation were completed only in 1896. Meanwhile the French geodesists had accomplished in 1879 the junction of Algeria to Spain, with the help of the geodesists of the Madrid Institute headed by the late Carlos Ibañez Ibáñez de Ibero (1825-1891), who had been president of the International Geodetic Association (now called International Association of Geodesy), first president of the International Committee for Weights and Measures and one of the 81 initial members of the International Statistical Institute. [10] Until Hayford ellipsoid was calculated in 1910, vertical deflections were considered as random errors. [11] Plumb line deviations were identified by Jean Le Rond d'Alembert as an important source of error in geodetic surveys as early as 1756, a few years later, in 1828, Carl Friedrich Gauss proposed the concept of geoid. [12] [13]

See also

Related Research Articles

<span class="mw-page-title-main">Geodesy</span> Science of measuring the shape, orientation, and gravity of the Earth and other astronomical bodies

Geodesy is the science of measuring and representing the geometry, gravity, and spatial orientation of the Earth in temporally varying 3D. It is called planetary geodesy when studying other astronomical bodies, such as planets or circumplanetary systems.

<span class="mw-page-title-main">Latitude</span> Geographic coordinate specifying north–south position

In geography, latitude is a coordinate that specifies the north–south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from –90° at the south pole to 90° at the north pole, with 0° at the Equator. Lines of constant latitude, or parallels, run east–west as circles parallel to the equator. Latitude and longitude are used together as a coordinate pair to specify a location on the surface of the Earth.

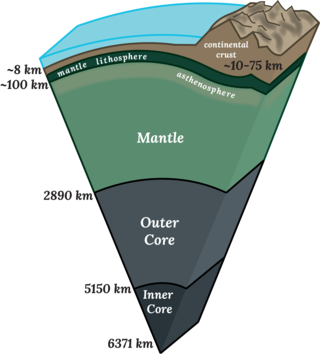
<span class="mw-page-title-main">Earth radius</span> Distance from the Earth surface to a point near its center

Earth radius is the distance from the center of Earth to a point on or near its surface. Approximating the figure of Earth by an Earth spheroid, the radius ranges from a maximum of nearly 6,378 km (3,963 mi) to a minimum of nearly 6,357 km (3,950 mi).

<span class="mw-page-title-main">Geoid</span> Ocean shape without winds and tides

The geoid is the shape that the ocean surface would take under the influence of the gravity of Earth, including gravitational attraction and Earth's rotation, if other influences such as winds and tides were absent. This surface is extended through the continents. According to Gauss, who first described it, it is the "mathematical figure of the Earth", a smooth but irregular surface whose shape results from the uneven distribution of mass within and on the surface of Earth. It can be known only through extensive gravitational measurements and calculations. Despite being an important concept for almost 200 years in the history of geodesy and geophysics, it has been defined to high precision only since advances in satellite geodesy in the late 20th century.

<span class="mw-page-title-main">Physical geodesy</span> Study of the physical properties of the Earths gravity field

Physical geodesy is the study of the physical properties of Earth's gravity and its potential field, with a view to their application in geodesy.

<span class="mw-page-title-main">World Geodetic System</span> Geodetic reference system

The World Geodetic System (WGS) is a standard used in cartography, geodesy, and satellite navigation including GPS. The current version, WGS 84, defines an Earth-centered, Earth-fixed coordinate system and a geodetic datum, and also describes the associated Earth Gravitational Model (EGM) and World Magnetic Model (WMM). The standard is published and maintained by the United States National Geospatial-Intelligence Agency.

<span class="mw-page-title-main">Figure of the Earth</span> Size and shape used to model the Earth for geodesy

Figure of the Earth is a term of art in geodesy that refers to the size and shape used to model Earth. The size and shape it refers to depend on context, including the precision needed for the model. A sphere is a well-known historical approximation of the figure of the Earth that is satisfactory for many purposes. Several models with greater accuracy have been developed so that coordinate systems can serve the precise needs of navigation, surveying, cadastre, land use, and various other concerns.

<span class="mw-page-title-main">Prime meridian (Greenwich)</span> Meridian passing through Greenwich, London

<span class="mw-page-title-main">U.S. National Geodetic Survey</span> U.S. federal surveying and mapping agency

The National Geodetic Survey (NGS) is a United States federal agency based in Washington, D.C. that defines and manages a national coordinate system, providing the foundation for transportation and communication, mapping and charting, and a large number of science and engineering applications. Since its founding in 1970, it has been part of the National Oceanic and Atmospheric Administration (NOAA), a division within the United States Department of Commerce.

<span class="mw-page-title-main">Geodetic datum</span> Reference frame for measuring location

A geodetic datum or geodetic system is a global datum reference or reference frame for precisely representing the position of locations on Earth or other planetary bodies by means of geodetic coordinates. Datums are crucial to any technology or technique based on spatial location, including geodesy, navigation, surveying, geographic information systems, remote sensing, and cartography. A horizontal datum is used to measure a location across the Earth's surface, in latitude and longitude or another coordinate system; a vertical datum is used to measure the elevation or depth relative to a standard origin, such as mean sea level (MSL). Since the rise of the global positioning system (GPS), the ellipsoid and datum WGS 84 it uses has supplanted most others in many applications. The WGS 84 is intended for global use, unlike most earlier datums.

<span class="mw-page-title-main">Arc measurement</span>

Arc measurement, sometimes degree measurement, is the astrogeodetic technique of determining of the radius of Earth – more specifically, the local Earth radius of curvature of the figure of the Earth – by relating the latitude difference and the geographic distance surveyed between two locations on Earth's surface. The most common variant involves only astronomical latitudes and the meridian arc length and is called meridian arc measurement; other variants may involve only astronomical longitude or both geographic coordinates . Arc measurement campaigns in Europe were the precursors to the International Association of Geodesy (IAG).

Geodetic astronomy or astronomical geodesy (astro-geodesy) is the application of astronomical methods into geodetic networks and other technical projects of geodesy.

<span class="mw-page-title-main">Zenith camera</span>

A zenith camera is an astrogeodetic telescope used today primarily for the local surveys of Earth's gravity field. Zenith cameras are designed as transportable field instruments for the direct observation of the plumb line and vertical deflections.

The orthometric height is the vertical distance H along the plumb line from a point of interest to a reference surface known as the geoid, the vertical datum that approximates mean sea level. Orthometric height is one of the scientific formalizations of a laypersons' "height above sea level", along with other types of heights in Geodesy.

Mikhail Sergeevich Molodenskii was a Soviet physical geodesist. He was once said to be "probably the only geodesist who would have deserved a Nobel prize".

<span class="mw-page-title-main">North American Datum</span> Reference frame for geodesy on the continent

The North American Datum (NAD) is the horizontal datum now used to define the geodetic network in North America. A datum is a formal description of the shape of the Earth along with an "anchor" point for the coordinate system. In surveying, cartography, and land-use planning, two North American Datums are in use for making lateral or "horizontal" measurements: the North American Datum of 1927 (NAD 27) and the North American Datum of 1983 (NAD 83). Both are geodetic reference systems based on slightly different assumptions and measurements.

The Bessel ellipsoid is an important reference ellipsoid of geodesy. It is currently used by several countries for their national geodetic surveys, but will be replaced in the next decades by modern ellipsoids of satellite geodesy.

<span class="mw-page-title-main">Earth ellipsoid</span> Shape of planet Earth

An Earth ellipsoid or Earth spheroid is a mathematical figure approximating the Earth's form, used as a reference frame for computations in geodesy, astronomy, and the geosciences. Various different ellipsoids have been used as approximations.

<span class="mw-page-title-main">Irene Fischer</span> Austrian-American mathematician and geodesist

Irene Kaminka Fischer was an Austrian-American mathematician and geodesist. She was a member of the National Academy of Engineering, a Fellow of the American Geophysical Union, and inductee of the National Imagery and Mapping Agency Hall of Fame. Fischer became one of two internationally known women scientists in the field of geodesy during the golden age of the Project Mercury and the Apollo program. Her Mercury datum, as well as her work on the lunar parallax, were instrumental in conducting these missions. "In his preface to the ACSM publication, Fischer's former colleague, Bernard Chovitz, referred to her as one of the most renowned geodesists of the third quarter of the twentieth century. Yet this fact alone makes her one of the most renowned geodesists of all times, because, according to Chovitz, the third quarter of the twentieth century witnessed "the transition of geodesy from a regional to a global enterprise."

<span class="mw-page-title-main">Carlos Ibáñez e Ibáñez de Ibero</span> 1st Marquis of Mulhacén

Carlos Ibáñez e Ibáñez de Ibero, 1st Marquis of Mulhacén, was a Spanish divisional general and geodesist. He represented Spain at the 1875 Conference of the Metre Convention and was the first president of the International Committee for Weights and Measures. As a forerunner geodesist and president of the International Geodetic Association, he played a leading role in the worldwide dissemination of the metric system. His activities resulted in the distribution of a platinum and iridium prototype of the metre to all States parties to the Metre Convention during the first meeting of the General Conference on Weights and Measures in 1889. These prototypes defined the metre right up until 1960.

References

  1. ↑ Hirt, C.; Bürki, B.; Somieski, A.; Seeber, G. N. (2010). "Modern Determination of Vertical Deflections Using Digital Zenith Cameras" (PDF). Journal of Surveying Engineering. 136: 1–12. doi:10.1061/(ASCE)SU.1943-5428.0000009. hdl: 20.500.11937/34194 .
  2. ↑ Malys, Stephen; Seago, John H.; Palvis, Nikolaos K.; Seidelmann, P. Kenneth; Kaplan, George H. (1 August 2015). "Why the Greenwich meridian moved". Journal of Geodesy. 89 (12): 1263. Bibcode:2015JGeod..89.1263M. doi: 10.1007/s00190-015-0844-y .
  3. ↑ "Arc of the Meridian". Astronomical Society of South Africa. Retrieved 27 August 2020.
  4. ↑ Warner, Brian (1 April 2002). "Lacaille 250 years on". Astronomy and Geophysics. 43 (2): 2.25–2.26. doi: 10.1046/j.1468-4004.2002.43225.x .
  5. ↑ Alder, K. (2002). The Measure of All Things: The Seven-year Odyssey and Hidden Error that Transformed the World. Free Press. ISBN   978-0-7432-1675-3 . Retrieved 2020-08-02.
  6. ↑ Jean-Étienne Duby, Rapport sur les travaux de la Société de Physique et d’Histoire naturelle de Genève de juillet 1860 à juin 1861 par M. le Pasteur Duby. Lu à la séance du 13 juin 1861, in Mémoires de la Société de physique et d’histoire naturelle de Genève, 16 (1861-1862), 196-197.
  7. ↑ Vaníček, Petr; Foroughi, Ismael (2019). "How gravity field shortened our metre". Journal of Geodesy. 93 (9): 1821–1827. Bibcode:2019JGeod..93.1821V. doi:10.1007/s00190-019-01257-7. ISSN   0949-7714. S2CID   146099564.
  8. ↑ Levallois, Jean-Jacques (1991). "La méridienne de Dunkerque à Barcelone et la déterminiation du mètre (1972-1799)". E-Periodica (in French). doi:10.5169/seals-234595 . Retrieved 2022-12-23.
  9. ↑ Hirsch, Adolphe (1865). "Sur les progrès des travaux géodésiques en Europe". E-Periodica (in French). doi:10.5169/seals-88030 . Retrieved 2022-12-23.
  10. ↑ Clarke, Alexander Ross; Helmert, Friedrich Robert (1911). "Earth, Figure of the"  . Encyclopædia Britannica . Vol. 8 (11th ed.). pp. 801–813. see page 811
  11. ↑ Géodésie in Encyclopedia Universalis. Encyclopedia Universalis. 1996. pp. Vol 10, p. 302. ISBN   978-2-85229-290-1. OCLC   36747385.
  12. ↑ d'Alembert, Jean Le Rond (1756). "Article Figure de la Terre, (Astron. Géog. Physiq. & Méch.), vol. VI (1756), p. 749b–761b". enccre.academie-sciences.fr. Retrieved 2022-12-23.
  13. ↑ US Department of Commerce, National Oceanic and Atmospheric Administration. "What is the geoid?". geodesy.noaa.gov. Retrieved 2022-12-23.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.