
In psychology, decision-making is regarded as the cognitive process resulting in the selection of a belief or a course of action among several possible alternative options, it could be either rational or irrational. Decision-making process is a reasoning process based on assumptions of values, preferences and beliefs of the decision-maker. Every decision-making process produces a final choice, which may or may not prompt action.
Sensitivity analysis is the study of how the uncertainty in the output of a mathematical model or system can be divided and allocated to different sources of uncertainty in its inputs. A related practice is uncertainty analysis, which has a greater focus on uncertainty quantification and propagation of uncertainty; ideally, uncertainty and sensitivity analysis should be run in tandem.

Multiple-criteria decision-making (MCDM) or multiple-criteria decision analysis (MCDA) is a sub-discipline of operations research that explicitly evaluates multiple conflicting criteria in decision making. Conflicting criteria are typical in evaluating options: cost or price is usually one of the main criteria, and some measure of quality is typically another criterion, easily in conflict with the cost. In purchasing a car, cost, comfort, safety, and fuel economy may be some of the main criteria we consider – it is unusual that the cheapest car is the most comfortable and the safest one. In portfolio management, managers are interested in getting high returns while simultaneously reducing risks; however, the stocks that have the potential of bringing high returns typically carry high risk of losing money. In a service industry, customer satisfaction and the cost of providing service are fundamental conflicting criteria.
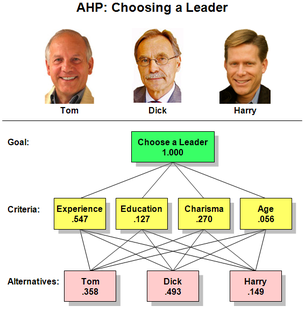
The analytic hierarchy process (AHP), also analytical hierarchy process, is a structured technique for organizing and analyzing complex decisions, based on mathematics and psychology. It was developed by Thomas L. Saaty in the 1970s; Saaty partnered with Ernest Forman to develop Expert Choice software in 1983, and AHP has been extensively studied and refined since then. It represents an accurate approach to quantifying the weights of decision criteria. Individual experts’ experiences are utilized to estimate the relative magnitudes of factors through pair-wise comparisons. Each of the respondents compares the relative importance each pair of items using a specially designed questionnaire.
The decision-matrix method, also Pugh method or Pugh concept selection, invented by Stuart Pugh, is a qualitative technique used to rank the multi-dimensional options of an option set. It is frequently used in engineering for making design decisions but can also be used to rank investment options, vendor options, product options or any other set of multidimensional entities.
The rational planning model is a model of the planning process involving a number of rational actions or steps. Taylor (1998) outlines five steps, as follows:
The analytic network process (ANP) is a more general form of the analytic hierarchy process (AHP) used in multi-criteria decision analysis.

The Paradox of Choice – Why More Is Less is a book written by American psychologist Barry Schwartz and first published in 2004 by Harper Perennial. In the book, Schwartz argues that eliminating consumer choices can greatly reduce anxiety for shoppers. The book analyses the behavior of different types of people facing the rich choice. This book demonstrates to us how the dramatic explosion in choice—from the mundane to the profound challenges of balancing career, family, and individual needs—has paradoxically become a problem instead of a solution and how our obsession with choice encourages us to seek that which makes us feel worse.
In applied mathematics and decision making, the aggregated indices randomization method (AIRM) is a modification of a well-known aggregated indices method, targeting complex objects subjected to multi-criteria estimation under uncertainty. AIRM was first developed by the Russian naval applied mathematician Aleksey Krylov around 1908.
Decision-making software is software for computer applications that help individuals and organisations make choices and take decisions, typically by ranking, prioritizing or choosing from a number of options.
Robust decision-making (RDM) is an iterative decision analytic framework that aims to help identify potential robust strategies, characterize the vulnerabilities of such strategies, and evaluate the tradeoffs among them. RDM focuses on informing decisions under conditions of what is called "deep uncertainty", that is, conditions where the parties to a decision do not know or do not agree on the system model(s) relating actions to consequences or the prior probability distributions for the key input parameters to those model(s).
In decision theory, the weighted sum model (WSM), also called weighted linear combination (WLC) or simple additive weighting (SAW), is the best known and simplest multi-criteria decision analysis (MCDA) / multi-criteria decision making method for evaluating a number of alternatives in terms of a number of decision criteria.
The weighted product model (WPM) is a popular multi-criteria decision analysis (MCDA) / multi-criteria decision making (MCDM) method. It is similar to the weighted sum model (WSM). The main difference is that instead of addition in the main mathematical operation now there is multiplication.
The decision-making paradox is a phenomenon related to decision-making and the quest for determining reliable decision-making methods. It was first described in 1989, and has been recognized in the related literature as a fundamental paradox in multi-criteria decision analysis (MCDA), multi-criteria decision making (MCDM) and decision analysis since then.
In decision-making, a rank reversal is a change in the rank ordering of the preferability of alternative possible decisions when, for example, the method of choosing changes or the set of other available alternatives changes. The issue of rank reversals lies at the heart of many debates in decision-making and multi-criteria decision-making, in particular.
Potentially All Pairwise RanKings of all possible Alternatives (PAPRIKA) is a method for multi-criteria decision making (MCDM) or conjoint analysis, as implemented by decision-making software and conjoint analysis products 1000minds and MeenyMo.
This is a worked-through example showing the use of the analytic hierarchy process (AHP) in a practical decision situation.
The Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) is a multi-criteria decision analysis method, which was originally developed by Ching-Lai Hwang and Yoon in 1981 with further developments by Yoon in 1987, and Hwang, Lai and Liu in 1993. TOPSIS is based on the concept that the chosen alternative should have the shortest geometric distance from the positive ideal solution (PIS) and the longest geometric distance from the negative ideal solution (NIS).
The VIKOR method is a multi-criteria decision making (MCDM) or multi-criteria decision analysis method. It was originally developed by Serafim Opricovic to solve decision problems with conflicting and noncommensurable criteria, assuming that compromise is acceptable for conflict resolution, the decision maker wants a solution that is the closest to the ideal, and the alternatives are evaluated according to all established criteria. VIKOR ranks alternatives and determines the solution named compromise that is the closest to the ideal.
Best Worst Method (BWM) is a multi-criteria decision-making (MCDM) method which was proposed by Dr. Jafar Rezaei in 2015. The method is used to evaluate a set of alternatives with respect to a set of decision criteria. The BWM is based on a systematic pairwise comparison of the decision criteria. That is, after identifying the decision criteria by the decision-maker (DM), two criteria are selected by the DM: the best criterion and the worst criterion. The best criterion is the one which has the most important role in making the decision, while the worst criterion has the opposite role. The DM then gives his/her preferences of the best criterion over all the other criteria and also his/her preferences of all the criteria over the worst criterion using a number from a predefined scale. These two sets of pairwise comparisons are used as input for an optimization problem, the optimal results of which are the weights of the criteria. The salient feature of the BWM is that it uses a structured way to generate the pairwise comparisons which leads to reliable results.



