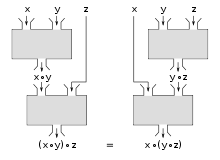
In mathematics, a binary operation or dyadic operation is a rule for combining two elements to produce another element. More formally, a binary operation is an operation of arity two.
In mathematics, the greatest common divisor (GCD) of two or more integers, which are not all zero, is the largest positive integer that divides each of the integers. For two integers x, y, the greatest common divisor of x and y is denoted . For example, the GCD of 8 and 12 is 4, that is, gcd(8, 12) = 4.
In algebra, a homomorphism is a structure-preserving map between two algebraic structures of the same type. The word homomorphism comes from the Ancient Greek language: ὁμός meaning "same" and μορφή meaning "form" or "shape". However, the word was apparently introduced to mathematics due to a (mis)translation of German ähnlich meaning "similar" to ὁμός meaning "same". The term "homomorphism" appeared as early as 1892, when it was attributed to the German mathematician Felix Klein (1849–1925).

In arithmetic and number theory, the least common multiple, lowest common multiple, or smallest common multiple of two integers a and b, usually denoted by lcm(a, b), is the smallest positive integer that is divisible by both a and b. Since division of integers by zero is undefined, this definition has meaning only if a and b are both different from zero. However, some authors define lcm(a, 0) as 0 for all a, since 0 is the only common multiple of a and 0.

In mathematics, exponentiation is an operation involving two numbers: the base and the exponent or power. Exponentiation is written as bn, where b is the base and n is the power; this is pronounced as "b (raised) to the n". When n is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, bn is the product of multiplying n bases:
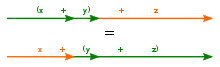
In mathematics, the distributive property of binary operations is a generalization of the distributive law, which asserts that the equality

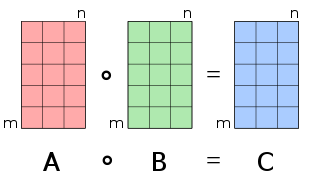
In mathematics, particularly in linear algebra, matrix multiplication is a binary operation that produces a matrix from two matrices. For matrix multiplication, the number of columns in the first matrix must be equal to the number of rows in the second matrix. The resulting matrix, known as the matrix product, has the number of rows of the first and the number of columns of the second matrix. The product of matrices A and B is denoted as AB.

In mathematics, the complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign. That is, if and are real numbers then the complex conjugate of is The complex conjugate of is often denoted as or .
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero; the term usually refers to square matrices. Elements of the main diagonal can either be zero or nonzero. An example of a 2×2 diagonal matrix is , while an example of a 3×3 diagonal matrix is. An identity matrix of any size, or any multiple of it is a diagonal matrix called scalar matrix, for example, . In geometry, a diagonal matrix may be used as a scaling matrix, since matrix multiplication with it results in changing scale (size) and possibly also shape; only a scalar matrix results in uniform change in scale.
In mathematics, Knuth's up-arrow notation is a method of notation for very large integers, introduced by Donald Knuth in 1976.

In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Perhaps most familiar as a property of arithmetic, e.g. "3 + 4 = 4 + 3" or "2 × 5 = 5 × 2", the property can also be used in more advanced settings. The name is needed because there are operations, such as division and subtraction, that do not have it ; such operations are not commutative, and so are referred to as noncommutative operations. The idea that simple operations, such as the multiplication and addition of numbers, are commutative was for many years implicitly assumed. Thus, this property was not named until the 19th century, when mathematics started to become formalized. A similar property exists for binary relations; a binary relation is said to be symmetric if the relation applies regardless of the order of its operands; for example, equality is symmetric as two equal mathematical objects are equal regardless of their order.
In mathematics, coalgebras or cogebras are structures that are dual to unital associative algebras. The axioms of unital associative algebras can be formulated in terms of commutative diagrams. Turning all arrows around, one obtains the axioms of coalgebras. Every coalgebra, by duality, gives rise to an algebra, but not in general the other way. In finite dimensions, this duality goes in both directions.
In abstract algebra, a semiring is an algebraic structure. It is a generalization of a ring, dropping the requirement that each element must have an additive inverse. At the same time, it is a generalization of bounded distributive lattices.
The Paillier cryptosystem, invented by and named after Pascal Paillier in 1999, is a probabilistic asymmetric algorithm for public key cryptography. The problem of computing n-th residue classes is believed to be computationally difficult. The decisional composite residuosity assumption is the intractability hypothesis upon which this cryptosystem is based.
In category theory, a branch of mathematics, a pushout is the colimit of a diagram consisting of two morphisms f : Z → X and g : Z → Y with a common domain. The pushout consists of an object P along with two morphisms X → P and Y → P that complete a commutative square with the two given morphisms f and g. In fact, the defining universal property of the pushout essentially says that the pushout is the "most general" way to complete this commutative square. Common notations for the pushout are and .
In mathematics, a GCD domain is an integral domain R with the property that any two elements have a greatest common divisor (GCD); i.e., there is a unique minimal principal ideal containing the ideal generated by two given elements. Equivalently, any two elements of R have a least common multiple (LCM).
In mathematics, specifically abstract algebra, the opposite of a ring is another ring with the same elements and addition operation, but with the multiplication performed in the reverse order. More explicitly, the opposite of a ring (R, +, ⋅) is the ring (R, +, ∗) whose multiplication ∗ is defined by a ∗ b = b⋅a for all a, b in R. The opposite ring can be used to define multimodules, a generalization of bimodules. They also help clarify the relationship between left and right modules (see § Properties).
In mathematical logic, Skolem arithmetic is the first-order theory of the natural numbers with multiplication, named in honor of Thoralf Skolem. The signature of Skolem arithmetic contains only the multiplication operation and equality, omitting the addition operation entirely.
In mathematics, the Hadamard product is a binary operation that takes in two matrices of the same dimensions and returns a matrix of the multiplied corresponding elements. This operation can be thought as a "naive matrix multiplication" and is different from the matrix product. It is attributed to, and named after, either French mathematician Jacques Hadamard or German mathematician Issai Schur.
In the theory of vertex algebras, the Zhu algebra and the closely related C2-algebra, introduced by Yongchang Zhu in his PhD thesis, are two associative algebras canonically constructed from a given vertex operator algebra. Many important representation theoretic properties of the vertex algebra are logically related to properties of its Zhu algebra or C2-algebra.