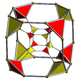
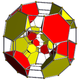
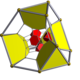
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral.

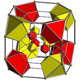
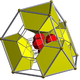
In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is a polyhedron with eight triangular, six square, and twelve rectangular faces. There are 24 identical vertices, with one triangle, one square, and two rectangles meeting at each one. If all the rectangles are themselves square, it is an Archimedean solid. The polyhedron has octahedral symmetry, like the cube and octahedron. Its dual is called the deltoidal icositetrahedron or trapezoidal icositetrahedron, although its faces are not really true trapezoids.

In four-dimensional geometry, a runcinated 5-cell is a convex uniform 4-polytope, being a runcination of the regular 5-cell.

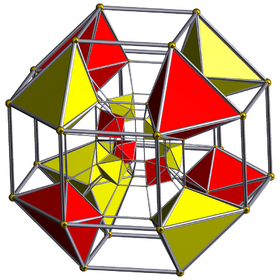
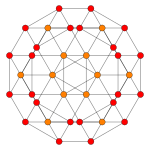
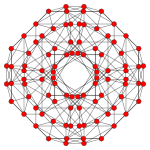
In four-dimensional geometry, a runcinated tesseract is a convex uniform 4-polytope, being a runcination of the regular tesseract.

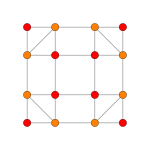
The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway called this honeycomb a cubille.

The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2.

In hyperbolic geometry, the order-5 cubic honeycomb is one of four compact regular space-filling tessellations in hyperbolic 3-space. With Schläfli symbol {4,3,5}, it has five cubes {4,3} around each edge, and 20 cubes around each vertex. It is dual with the order-4 dodecahedral honeycomb.

In geometry, a truncated 24-cell is a uniform 4-polytope formed as the truncation of the regular 24-cell.
In geometry, a truncated tesseract is a uniform 4-polytope formed as the truncation of the regular tesseract.
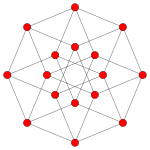
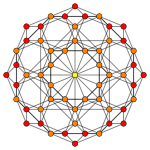
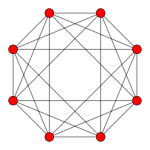
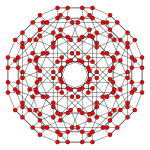
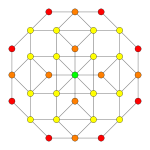
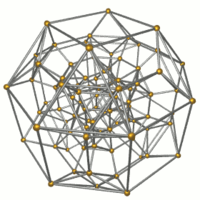
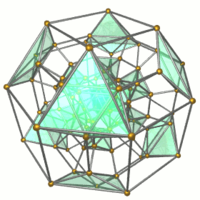
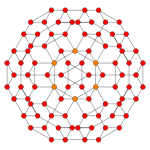
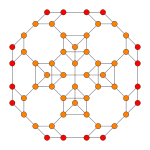
In geometry, the rectified tesseract, rectified 8-cell is a uniform 4-polytope bounded by 24 cells: 8 cuboctahedra, and 16 tetrahedra. It has half the vertices of a runcinated tesseract, with its construction, called a runcic tesseract.

In geometry, a truncated 5-cell is a uniform 4-polytope formed as the truncation of the regular 5-cell.

In four-dimensional geometry, a cantellated 5-cell is a convex uniform 4-polytope, being a cantellation of the regular 5-cell.

In four-dimensional geometry, a cantellated 24-cell is a convex uniform 4-polytope, being a cantellation of the regular 24-cell.

In four-dimensional geometry, a runcinated 24-cell is a convex uniform 4-polytope, being a runcination of the regular 24-cell.

In four-dimensional geometry, a cantellated 120-cell is a convex uniform 4-polytope, being a cantellation of the regular 120-cell.

In four-dimensional geometry, a runcinated 120-cell is a convex uniform 4-polytope, being a runcination of the regular 120-cell.

In five-dimensional geometry, a stericated 5-simplex is a convex uniform 5-polytope with fourth-order truncations (sterication) of the regular 5-simplex.

In five-dimensional geometry, a cantellated 5-simplex is a convex uniform 5-polytope, being a cantellation of the regular 5-simplex.