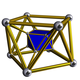
In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.

A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral.

In geometry, an octahedron is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.

In geometry, a prism is a polyhedron comprising an n-sided polygon base, a second base which is a translated copy of the first, and n other faces, necessarily all parallelograms, joining corresponding sides of the two bases. All cross-sections parallel to the bases are translations of the bases. Prisms are named after their bases, e.g. a prism with a pentagonal base is called a pentagonal prism. Prisms are a subclass of prismatoids.

In geometry, the Schläfli symbol is a notation of the form that defines regular polytopes and tessellations.

In geometry, the triangular bipyramid is the hexahedron with six triangular faces, constructed by attaching two tetrahedrons face-to-face. The same shape is also called the triangular dipyramid or trigonal bipyramid. If these tetrahedrons are regular, all faces of triangular bipyramid are equilateral. It is an example of a deltahedron and of a Johnson solid.

The triaugmented triangular prism, in geometry, is a convex polyhedron with 14 equilateral triangles as its faces. It can be constructed from a triangular prism by attaching equilateral square pyramids to each of its three square faces. The same shape is also called the tetrakis triangular prism, tricapped trigonal prism, tetracaidecadeltahedron, or tetrakaidecadeltahedron; these last names mean a polyhedron with 14 triangular faces. It is an example of a deltahedron and of a Johnson solid.

In geometry, the pentagonal bipyramid is a polyhedron with 10 triangular faces. It is constructed by attaching two pentagonal pyramids to each of their bases. If the triangular faces are equilateral, the pentagonal bipyramid is an example of deltahedra, and of Johnson solid.

In geometry, the elongated triangular pyramid is one of the Johnson solids. As the name suggests, it can be constructed by elongating a tetrahedron by attaching a triangular prism to its base. Like any elongated pyramid, the resulting solid is topologically self-dual.

In geometry, the elongated square bipyramid is the polyhedron constructed by attaching two equilateral square pyramids onto a cube's faces that are opposite each other. It can also be seen as 4 lunes linked together with squares to squares and triangles to triangles. It is also been named the pencil cube or 12-faced pencil cube due to its shape.

In geometry, the elongated triangular orthobicupola or cantellated triangular prism is a polyhedron constructed by attaching two regular triangular cupola into the base of a regular hexagonal prism. It is an example of Johnson solid.
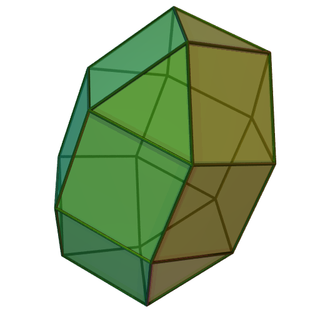
In geometry, the elongated triangular gyrobicupola is a polyhedron constructed by attaching two regular triangular cupolas to the base of a regular hexagonal prism, with one of them rotated in . It is an example of Johnson solid.

In geometry, a uniform 4-polytope is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons.

In geometry, a uniform polyhedron has regular polygons as faces and is vertex-transitive. It follows that all vertices are congruent.

In geometry, the hexagonal prism is a prism with hexagonal base. Prisms are polyhedrons; this polyhedron has 8 faces, 18 edges, and 12 vertices.

The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway called this honeycomb a cubille.
In geometry, a near-miss Johnson solid is a strictly convex polyhedron whose faces are close to being regular polygons but some or all of which are not precisely regular. Thus, it fails to meet the definition of a Johnson solid, a polyhedron whose faces are all regular, though it "can often be physically constructed without noticing the discrepancy" between its regular and irregular faces. The precise number of near-misses depends on how closely the faces of such a polyhedron are required to approximate regular polygons.

The triangular prismatic honeycomb or triangular prismatic cellulation is a space-filling tessellation in Euclidean 3-space. It is composed entirely of triangular prisms.