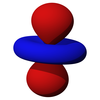
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively charged proton and a single negatively charged electron bound to the nucleus by the Coulomb force. Atomic hydrogen constitutes about 75% of the baryonic mass of the universe.

In mathematics and physical science, spherical harmonics are special functions defined on the surface of a sphere. They are often employed in solving partial differential equations in many scientific fields.
Slater-type orbitals (STOs) are functions used as atomic orbitals in the linear combination of atomic orbitals molecular orbital method. They are named after the physicist John C. Slater, who introduced them in 1930.
In computational chemistry and molecular physics, Gaussian orbitals are functions used as atomic orbitals in the LCAO method for the representation of electron orbitals in molecules and numerous properties that depend on these.
In classical mechanics, the Laplace–Runge–Lenz (LRL) vector is a vector used chiefly to describe the shape and orientation of the orbit of one astronomical body around another, such as a binary star or a planet revolving around a star. For two bodies interacting by Newtonian gravity, the LRL vector is a constant of motion, meaning that it is the same no matter where it is calculated on the orbit; equivalently, the LRL vector is said to be conserved. More generally, the LRL vector is conserved in all problems in which two bodies interact by a central force that varies as the inverse square of the distance between them; such problems are called Kepler problems.
In physics, the Clebsch–Gordan (CG) coefficients are numbers that arise in angular momentum coupling in quantum mechanics. They appear as the expansion coefficients of total angular momentum eigenstates in an uncoupled tensor product basis. In more mathematical terms, the CG coefficients are used in representation theory, particularly of compact Lie groups, to perform the explicit direct sum decomposition of the tensor product of two irreducible representations. The name derives from the German mathematicians Alfred Clebsch and Paul Gordan, who encountered an equivalent problem in invariant theory.
A multipole expansion is a mathematical series representing a function that depends on angles—usually the two angles used in the spherical coordinate system for three-dimensional Euclidean space, . Similarly to Taylor series, multipole expansions are useful because oftentimes only the first few terms are needed to provide a good approximation of the original function. The function being expanded may be real- or complex-valued and is defined either on , or less often on for some other .
In quantum physics, the spin–orbit interaction is a relativistic interaction of a particle's spin with its motion inside a potential. A key example of this phenomenon is the spin–orbit interaction leading to shifts in an electron's atomic energy levels, due to electromagnetic interaction between the electron's magnetic dipole, its orbital motion, and the electrostatic field of the positively charged nucleus. This phenomenon is detectable as a splitting of spectral lines, which can be thought of as a Zeeman effect product of two relativistic effects: the apparent magnetic field seen from the electron perspective and the magnetic moment of the electron associated with its intrinsic spin. A similar effect, due to the relationship between angular momentum and the strong nuclear force, occurs for protons and neutrons moving inside the nucleus, leading to a shift in their energy levels in the nucleus shell model. In the field of spintronics, spin–orbit effects for electrons in semiconductors and other materials are explored for technological applications. The spin–orbit interaction is one cause of magnetocrystalline anisotropy and the spin Hall effect.
In quantum mechanics, the angular momentum operator is one of several related operators analogous to classical angular momentum. The angular momentum operator plays a central role in the theory of atomic and molecular physics and other quantum problems involving rotational symmetry. Such an operator is applied to a mathematical representation of the physical state of a system and yields an angular momentum value if the state has a definite value for it. In both classical and quantum mechanical systems, angular momentum is one of the three fundamental properties of motion.
In quantum mechanics, Landau quantization refers to the quantization of the cyclotron orbits of charged particles in a uniform magnetic field. As a result, the charged particles can only occupy orbits with discrete, equidistant energy values, called Landau levels. These levels are degenerate, with the number of electrons per level directly proportional to the strength of the applied magnetic field. It is named after the Soviet physicist Lev Landau.
In quantum mechanics, the spinor spherical harmonics are special functions defined over the sphere. The spinor spherical harmonics are the natural spinor analog of the vector spherical harmonics. While the standard spherical harmonics are a basis for the angular momentum operator, the spinor spherical harmonics are a basis for the total angular momentum operator. These functions are used in analytical solutions to Dirac equation in a radial potential. The spinor spherical harmonics are sometimes called Pauli central field spinors, in honor to Wolfgang Pauli who employed them in the solution of the hydrogen atom with spin–orbit interaction.
A hydrogen-like atom/ion (usually called a "hydrogenic atom") is any atomic nucleus bound to one electron and thus is isoelectronic with hydrogen. These atoms or ions can carry the positive charge , where is the atomic number of the atom. Examples of hydrogen-like atoms/ions are hydrogen itself, He+, Li2+, Be3+ and B4+. Because hydrogen-like atoms/ions are two-particle systems with an interaction depending only on the distance between the two particles, their (non-relativistic) Schrödinger equation can be solved in analytic form, as can the (relativistic) Dirac equation. The solutions are one-electron functions and are referred to as hydrogen-like atomic orbitals.
In physics and mathematics, the solid harmonics are solutions of the Laplace equation in spherical polar coordinates, assumed to be (smooth) functions . There are two kinds: the regular solid harmonics, which are well-defined at the origin and the irregular solid harmonics, which are singular at the origin. Both sets of functions play an important role in potential theory, and are obtained by rescaling spherical harmonics appropriately:
In mathematics, vector spherical harmonics (VSH) are an extension of the scalar spherical harmonics for use with vector fields. The components of the VSH are complex-valued functions expressed in the spherical coordinate basis vectors.
Spin is an intrinsic form of angular momentum carried by elementary particles, composite particles (hadrons), and atomic nuclei.
In linear algebra, a raising or lowering operator is an operator that increases or decreases the eigenvalue of another operator. In quantum mechanics, the raising operator is sometimes called the creation operator, and the lowering operator the annihilation operator. Well-known applications of ladder operators in quantum mechanics are in the formalisms of the quantum harmonic oscillator and angular momentum.

Symmetries in quantum mechanics describe features of spacetime and particles which are unchanged under some transformation, in the context of quantum mechanics, relativistic quantum mechanics and quantum field theory, and with applications in the mathematical formulation of the standard model and condensed matter physics. In general, symmetry in physics, invariance, and conservation laws, are fundamentally important constraints for formulating physical theories and models. In practice, they are powerful methods for solving problems and predicting what can happen. While conservation laws do not always give the answer to the problem directly, they form the correct constraints and the first steps to solving a multitude of problems.
In pure and applied mathematics, particularly quantum mechanics and computer graphics and their applications, a spherical basis is the basis used to express spherical tensors. The spherical basis closely relates to the description of angular momentum in quantum mechanics and spherical harmonic functions.
In pure and applied mathematics, quantum mechanics and computer graphics, a tensor operator generalizes the notion of operators which are scalars and vectors. A special class of these are spherical tensor operators which apply the notion of the spherical basis and spherical harmonics. The spherical basis closely relates to the description of angular momentum in quantum mechanics and spherical harmonic functions. The coordinate-free generalization of a tensor operator is known as a representation operator.
Molecular symmetry in physics and chemistry describes the symmetry present in molecules and the classification of molecules according to their symmetry. Molecular symmetry is a fundamental concept in the application of Quantum Mechanics in physics and chemistry, for example it can be used to predict or explain many of a molecule's properties, such as its dipole moment and its allowed spectroscopic transitions, without doing the exact rigorous calculations. To do this it is necessary to classify the states of the molecule using the irreducible representations from the character table of the symmetry group of the molecule. Among all the molecular symmetries, diatomic molecules show some distinct features and they are relatively easier to analyze.