
In condensed matter physics, a Bose–Einstein condensate (BEC) is a state of matter that is typically formed when a gas of bosons at very low densities is cooled to temperatures very close to absolute zero. Under such conditions, a large fraction of bosons occupy the lowest quantum state, at which microscopic quantum-mechanical phenomena, particularly wavefunction interference, become apparent macroscopically. More generally, condensation refers to the appearance of macroscopic occupation of one or several states: for example, in BCS theory, a superconductor is a condensate of Cooper pairs. As such, condensation can be associated with phase transition, and the macroscopic occupation of the state is the order parameter.
Positronium (Ps) is a system consisting of an electron and its anti-particle, a positron, bound together into an exotic atom, specifically an onium. Unlike hydrogen, the system has no protons. The system is unstable: the two particles annihilate each other to predominantly produce two or three gamma-rays, depending on the relative spin states. The energy levels of the two particles are similar to that of the hydrogen atom. However, because of the reduced mass, the frequencies of the spectral lines are less than half of those for the corresponding hydrogen lines.

The Standard Model of particle physics is the theory describing three of the four known fundamental forces in the universe and classifying all known elementary particles. It was developed in stages throughout the latter half of the 20th century, through the work of many scientists worldwide, with the current formulation being finalized in the mid-1970s upon experimental confirmation of the existence of quarks. Since then, proof of the top quark (1995), the tau neutrino (2000), and the Higgs boson (2012) have added further credence to the Standard Model. In addition, the Standard Model has predicted various properties of weak neutral currents and the W and Z bosons with great accuracy.

The charm quark, charmed quark, or c quark is an elementary particle found in composite subatomic particles called hadrons such as the J/psi meson and the charmed baryons created in particle accelerator collisions. Several bosons, including the W and Z bosons and the Higgs boson, can decay into charm quarks. All charm quarks carry charm, a quantum number. This second generation particle is the third-most-massive quark with a mass of 1.27±0.02 GeV/c2 as measured in 2022 and a charge of +2/3 e.
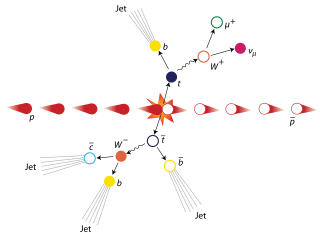
The top quark, sometimes also referred to as the truth quark, is the most massive of all observed elementary particles. It derives its mass from its coupling to the Higgs Boson. This coupling is very close to unity; in the Standard Model of particle physics, it is the largest (strongest) coupling at the scale of the weak interactions and above. The top quark was discovered in 1995 by the CDF and DØ experiments at Fermilab.

Technicolor theories are models of physics beyond the Standard Model that address electroweak gauge symmetry breaking, the mechanism through which W and Z bosons acquire masses. Early technicolor theories were modelled on quantum chromodynamics (QCD), the "color" theory of the strong nuclear force, which inspired their name.

Certain systems can achieve negative thermodynamic temperature; that is, their temperature can be expressed as a negative quantity on the Kelvin or Rankine scales. This should be distinguished from temperatures expressed as negative numbers on non-thermodynamic Celsius or Fahrenheit scales, which are nevertheless higher than absolute zero. A system with a truly negative temperature on the Kelvin scale is hotter than any system with a positive temperature. If a negative-temperature system and a positive-temperature system come in contact, heat will flow from the negative- to the positive-temperature system. A standard example of such a system is population inversion in laser physics.
A bound state is a composite of two or more fundamental building blocks, such as particles, atoms, or bodies, that behaves as a single object and in which energy is required to split them.

In theoretical physics, the hierarchy problem is the problem concerning the large discrepancy between aspects of the weak force and gravity. There is no scientific consensus on why, for example, the weak force is 1024 times stronger than gravity.
In physics, a Feshbach resonance can occur upon collision of two slow atoms, when they temporarily stick together forming an unstable compound with short lifetime. It is a feature of many-body systems in which a bound state is achieved if the coupling(s) between at least one internal degree of freedom and the reaction coordinates, which lead to dissociation, vanish. The opposite situation, when a bound state is not formed, is a shape resonance. It is named after Herman Feshbach, a physicist at MIT.

Rudolf Grimm is an experimental physicist from Austria. His work centres on ultracold atoms and quantum gases. He was the first scientist worldwide who, with his team, succeeded in realizing a Bose–Einstein condensation of molecules.
In quantum electrodynamics, the anomalous magnetic moment of a particle is a contribution of effects of quantum mechanics, expressed by Feynman diagrams with loops, to the magnetic moment of that particle. The magnetic moment, also called magnetic dipole moment, is a measure of the strength of a magnetic source.
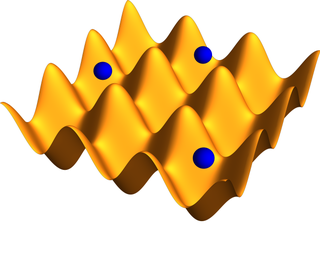
An optical lattice is formed by the interference of counter-propagating laser beams, creating a spatially periodic polarization pattern. The resulting periodic potential may trap neutral atoms via the Stark shift. Atoms are cooled and congregate at the potential extrema. The resulting arrangement of trapped atoms resembles a crystal lattice and can be used for quantum simulation.
The Bose–Hubbard model gives a description of the physics of interacting spinless bosons on a lattice. It is closely related to the Hubbard model that originated in solid-state physics as an approximate description of superconducting systems and the motion of electrons between the atoms of a crystalline solid. The model was introduced by Gersch and Knollman in 1963 in the context of granular superconductors. The model rose to prominence in the 1980s after it was found to capture the essence of the superfluid-insulator transition in a way that was much more mathematically tractable than fermionic metal-insulator models.
R is the ratio of the hadronic cross section to the muon cross section in electron–positron collisions:

Ultracold neutrons (UCN) are free neutrons which can be stored in traps made from certain materials. The storage is based on the reflection of UCN by such materials under any angle of incidence.

Superfluidity is the characteristic property of a fluid with zero viscosity which therefore flows without any loss of kinetic energy. When stirred, a superfluid forms vortices that continue to rotate indefinitely. Superfluidity occurs in two isotopes of helium when they are liquefied by cooling to cryogenic temperatures. It is also a property of various other exotic states of matter theorized to exist in astrophysics, high-energy physics, and theories of quantum gravity. The theory of superfluidity was developed by Soviet theoretical physicists Lev Landau and Isaak Khalatnikov.

A Borromean nucleus is an atomic nucleus comprising three bound components in which any subsystem of two components is unbound. This has the consequence that if one component is removed, the remaining two comprise an unbound resonance, so that the original nucleus is split into three parts.

When embedded in an atomic nucleus, neutrons are (usually) stable particles. Outside the nucleus, free neutrons are unstable and have a mean lifetime of 877.75+0.50
−0.44 s or 879.6±0.8 s. Therefore, the half-life for this process is 611±1 s.
The term Dirac matter refers to a class of condensed matter systems which can be effectively described by the Dirac equation. Even though the Dirac equation itself was formulated for fermions, the quasi-particles present within Dirac matter can be of any statistics. As a consequence, Dirac matter can be distinguished in fermionic, bosonic or anyonic Dirac matter. Prominent examples of Dirac matter are graphene and other Dirac semimetals, topological insulators, Weyl semimetals, various high-temperature superconductors with -wave pairing and liquid helium-3. The effective theory of such systems is classified by a specific choice of the Dirac mass, the Dirac velocity, the gamma matrices and the space-time curvature. The universal treatment of the class of Dirac matter in terms of an effective theory leads to a common features with respect to the density of states, the heat capacity and impurity scattering.






















