
In physics, interference is a phenomenon in which two waves combine by adding their displacement together at every single point in space and time, to form a resultant wave of greater, lower, or the same amplitude. Constructive and destructive interference result from the interaction of waves that are correlated or coherent with each other, either because they come from the same source or because they have the same or nearly the same frequency. Interference effects can be observed with all types of waves, for example, light, radio, acoustic, surface water waves, gravity waves, or matter waves.

Stimulated emission is the process by which an incoming photon of a specific frequency can interact with an excited atomic electron, causing it to drop to a lower energy level. The liberated energy transfers to the electromagnetic field, creating a new photon with a frequency, polarization, and direction of travel that are all identical to the photons of the incident wave. This is in contrast to spontaneous emission, which occurs at a characteristic rate for each of the atoms/oscillators in the upper energy state regardless of the external electromagnetic field.
In physics, coherence length is the propagation distance over which a coherent wave maintains a specified degree of coherence. Wave interference is strong when the paths taken by all of the interfering waves differ by less than the coherence length. A wave with a longer coherence length is closer to a perfect sinusoidal wave. Coherence length is important in holography and telecommunications engineering.
Fourier-transform spectroscopy is a measurement technique whereby spectra are collected based on measurements of the coherence of a radiative source, using time-domain or space-domain measurements of the radiation, electromagnetic or not. It can be applied to a variety of types of spectroscopy including optical spectroscopy, infrared spectroscopy, nuclear magnetic resonance (NMR) and magnetic resonance spectroscopic imaging (MRSI), mass spectrometry and electron spin resonance spectroscopy.
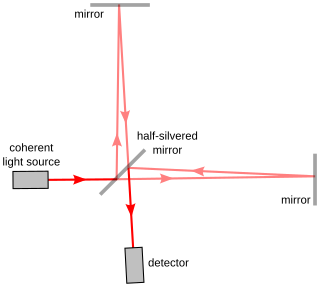
Interferometry is a technique which uses the interference of superimposed waves to extract information. Interferometry typically uses electromagnetic waves and is an important investigative technique in the fields of astronomy, fiber optics, engineering metrology, optical metrology, oceanography, seismology, spectroscopy, quantum mechanics, nuclear and particle physics, plasma physics, remote sensing, biomolecular interactions, surface profiling, microfluidics, mechanical stress/strain measurement, velocimetry, optometry, and making holograms.

In optics, a Fabry–Pérot interferometer (FPI) or etalon is an optical cavity made from two parallel reflecting surfaces. Optical waves can pass through the optical cavity only when they are in resonance with it. It is named after Charles Fabry and Alfred Perot, who developed the instrument in 1899. Etalon is from the French étalon, meaning "measuring gauge" or "standard".
In physics, two wave sources are coherent if their frequency and waveform are identical. Coherence is an ideal property of waves that enables stationary interference. It contains several distinct concepts, which are limiting cases that never quite occur in reality but allow an understanding of the physics of waves, and has become a very important concept in quantum physics. More generally, coherence describes all properties of the correlation between physical quantities of a single wave, or between several waves or wave packets.

In physics, the Mach–Zehnder interferometer is a device used to determine the relative phase shift variations between two collimated beams derived by splitting light from a single source. The interferometer has been used, among other things, to measure phase shifts between the two beams caused by a sample or a change in length of one of the paths. The apparatus is named after the physicists Ludwig Mach and Ludwig Zehnder; Zehnder's proposal in an 1891 article was refined by Mach in an 1892 article. Demonstrations of Mach–Zehnder interferometry with particles other than photons had been demonstrated as well in multiple experiments.

The Michelson interferometer is a common configuration for optical interferometry and was invented by the 19/20th-century American physicist Albert Abraham Michelson. Using a beam splitter, a light source is split into two arms. Each of those light beams is reflected back toward the beamsplitter which then combines their amplitudes using the superposition principle. The resulting interference pattern that is not directed back toward the source is typically directed to some type of photoelectric detector or camera. For different applications of the interferometer, the two light paths can be with different lengths or incorporate optical elements or even materials under test.
In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important. Its magnitude is either the wavenumber or angular wavenumber of the wave, and its direction is ordinarily the direction of wave propagation.

The Sagnac effect, also called Sagnac interference, named after French physicist Georges Sagnac, is a phenomenon encountered in interferometry that is elicited by rotation. The Sagnac effect manifests itself in a setup called a ring interferometer or Sagnac interferometer. A beam of light is split and the two beams are made to follow the same path but in opposite directions. On return to the point of entry the two light beams are allowed to exit the ring and undergo interference. The relative phases of the two exiting beams, and thus the position of the interference fringes, are shifted according to the angular velocity of the apparatus. In other words, when the interferometer is at rest with respect to a nonrotating frame, the light takes the same amount of time to traverse the ring in either direction. However, when the interferometer system is spun, one beam of light has a longer path to travel than the other in order to complete one circuit of the mechanical frame, and so takes longer, resulting in a phase difference between the two beams. Georges Sagnac set up this experiment in an attempt to prove the existence of the aether that Einstein's theory of special relativity had discarded.
In quantum optics, correlation functions are used to characterize the statistical and coherence properties of an electromagnetic field. The degree of coherence is the normalized correlation of electric fields; in its simplest form, termed . It is useful for quantifying the coherence between two electric fields, as measured in a Michelson or other linear optical interferometer. The correlation between pairs of fields, , typically is used to find the statistical character of intensity fluctuations. First order correlation is actually the amplitude-amplitude correlation and the second order correlation is the intensity-intensity correlation. It is also used to differentiate between states of light that require a quantum mechanical description and those for which classical fields are sufficient. Analogous considerations apply to any Bose field in subatomic physics, in particular to mesons.
The wave–particle duality relation, often loosely referred to as the Englert–Greenberger–Yasin duality relation, or the Englert–Greenberger relation, relates the visibility, , of interference fringes with the definiteness, or distinguishability, , of the photons' paths in quantum optics. As an inequality:
The van Cittert–Zernike theorem, named after physicists Pieter Hendrik van Cittert and Frits Zernike, is a formula in coherence theory that states that under certain conditions the Fourier transform of the intensity distribution function of a distant, incoherent source is equal to its complex visibility. This implies that the wavefront from an incoherent source will appear mostly coherent at large distances. Intuitively, this can be understood by considering the wavefronts created by two incoherent sources. If we measure the wavefront immediately in front of one of the sources, our measurement will be dominated by the nearby source. If we make the same measurement far from the sources, our measurement will no longer be dominated by a single source; both sources will contribute almost equally to the wavefront at large distances.
Self-mixing or back-injection laser interferometry is an interferometric technique in which a part of the light reflected by a vibrating target is reflected into the laser cavity, causing a modulation both in amplitude and in frequency of the emitted optical beam. In this way, the laser becomes sensitive to the distance traveled by the reflected beam thus becoming a distance, speed or vibration sensor. The advantage compared to a traditional measurement system is a lower cost thanks to the absence of collimation optics and external photodiodes.

As described here, white light interferometry is a non-contact optical method for surface height measurement on 3-D structures with surface profiles varying between tens of nanometers and a few centimeters. It is often used as an alternative name for coherence scanning interferometry in the context of areal surface topography instrumentation that relies on spectrally-broadband, visible-wavelength light.
Coherence is defined as the ability of waves to interfere. Intuitively, coherent waves have a well-defined constant phase relationship. However, an exclusive and extensive physical definition of coherence is more nuanced. Coherence functions, as introduced by Roy Glauber and others in the 1960s, capture the mathematics behind the intuition by defining correlation between the electric field components as coherence. These correlations between electric field components can be measured to arbitrary orders, hence leading to the concept of different orders of coherence. The coherence encountered in most optical experiments, including the classic Young's double slit experiment and Mach-Zehnder interferometer, is first order coherence. Robert Hanbury Brown and Richard Q. Twiss performed a correlation experiment in 1956, and brought to light a different kind of correlation between fields, namely the correlation of intensities, which correspond to second order coherence. Higher order coherences become relevant in photon-coincidence counting experiments. Orders of coherence can be measured using classical correlation functions or by using the quantum analogue of those functions, which take quantum mechanical description of electric field (operators) as input. While the quantum coherence functions might yield the same results as the classical functions, the underlying mechanism and description of the physical processes are fundamentally different because quantum interference deals with interference of possible histories while classical interference deals with interference of physical waves.
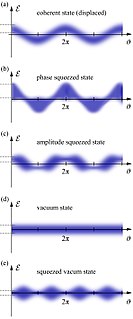
In quantum physics, light is in a squeezed state if its electric field strength Ԑ for some phases has a quantum uncertainty smaller than that of a coherent state. The term squeezing thus refers to a reduced quantum uncertainty. To obey Heisenberg's uncertainty relation, a squeezed state must also have phases at which the electric field uncertainty is anti-squeezed, i.e. larger than that of a coherent state. Since 2019, the gravitational-wave observatories LIGO and Virgo employ squeezed laser light, which has significantly increased the rate of observed gravitational-wave events.
SU(1,1) interferometry is a technique that uses parametric amplification for splitting and mixing of electromagnetic waves for precise estimation of phase change and achieves the Heisenberg limit of sensitivity with fewer optical elements than conventional interferometric techniques.





















