
Theoretical ecology is the scientific discipline devoted to the study of ecological systems using theoretical methods such as simple conceptual models, mathematical models, computational simulations, and advanced data analysis. Effective models improve understanding of the natural world by revealing how the dynamics of species populations are often based on fundamental biological conditions and processes. Further, the field aims to unify a diverse range of empirical observations by assuming that common, mechanistic processes generate observable phenomena across species and ecological environments. Based on biologically realistic assumptions, theoretical ecologists are able to uncover novel, non-intuitive insights about natural processes. Theoretical results are often verified by empirical and observational studies, revealing the power of theoretical methods in both predicting and understanding the noisy, diverse biological world.

In ecology, a niche is the match of a species to a specific environmental condition. It describes how an organism or population responds to the distribution of resources and competitors and how it in turn alters those same factors. "The type and number of variables comprising the dimensions of an environmental niche vary from one species to another [and] the relative importance of particular environmental variables for a species may vary according to the geographic and biotic contexts".
This glossary of ecology is a list of definitions of terms and concepts in ecology and related fields. For more specific definitions from other glossaries related to ecology, see Glossary of biology, Glossary of evolutionary biology, and Glossary of environmental science.

In ecology, the competitive exclusion principle, sometimes referred to as Gause's law, is a proposition that two species which compete for the same limited resource cannot coexist at constant population values. When one species has even the slightest advantage over another, the one with the advantage will dominate in the long term. This leads either to the extinction of the weaker competitor or to an evolutionary or behavioral shift toward a different ecological niche. The principle has been paraphrased in the maxim "complete competitors cannot coexist".
The Lotka–Volterra equations, also known as the Lotka–Volterra predator–prey model, are a pair of first-order nonlinear differential equations, frequently used to describe the dynamics of biological systems in which two species interact, one as a predator and the other as prey. The populations change through time according to the pair of equations:
Population dynamics is the type of mathematics used to model and study the size and age composition of populations as dynamical systems.

Population ecology is a sub-field of ecology that deals with the dynamics of species populations and how these populations interact with the environment, such as birth and death rates, and by immigration and emigration.

A metapopulation consists of a group of spatially separated populations of the same species which interact at some level. The term metapopulation was coined by Richard Levins in 1969 to describe a model of population dynamics of insect pests in agricultural fields, but the idea has been most broadly applied to species in naturally or artificially fragmented habitats. In Levins' own words, it consists of "a population of populations".
The competitive Lotka–Volterra equations are a simple model of the population dynamics of species competing for some common resource. They can be further generalised to the generalized Lotka–Volterra equation to include trophic interactions.

Character displacement is the phenomenon where differences among similar species whose distributions overlap geographically are accentuated in regions where the species co-occur, but are minimized or lost where the species' distributions do not overlap. This pattern results from evolutionary change driven by biological competition among species for a limited resource. The rationale for character displacement stems from the competitive exclusion principle, also called Gause's Law, which contends that to coexist in a stable environment two competing species must differ in their respective ecological niche; without differentiation, one species will eliminate or exclude the other through competition.
A Malthusian growth model, sometimes called a simple exponential growth model, is essentially exponential growth based on the idea of the function being proportional to the speed to which the function grows. The model is named after Thomas Robert Malthus, who wrote An Essay on the Principle of Population (1798), one of the earliest and most influential books on population.

Competition is an interaction between organisms or species in which both require a resource that is in limited supply. Competition lowers the fitness of both organisms involved since the presence of one of the organisms always reduces the amount of the resource available to the other.

Interspecific competition, in ecology, is a form of competition in which individuals of different species compete for the same resources in an ecosystem. This can be contrasted with mutualism, a type of symbiosis. Competition between members of the same species is called intraspecific competition.

An ecosystem model is an abstract, usually mathematical, representation of an ecological system, which is studied to better understand the real system.
A population model is a type of mathematical model that is applied to the study of population dynamics.
The generalized Lotka–Volterra equations are a set of equations which are more general than either the competitive or predator–prey examples of Lotka–Volterra types. They can be used to model direct competition and trophic relationships between an arbitrary number of species. Their dynamics can be analysed analytically to some extent. This makes them useful as a theoretical tool for modeling food webs. However, they lack features of other ecological models such as predator preference and nonlinear functional responses, and they cannot be used to model mutualism without allowing indefinite population growth.

Coexistence theory is a framework to understand how competitor traits can maintain species diversity and stave-off competitive exclusion even among similar species living in ecologically similar environments. Coexistence theory explains the stable coexistence of species as an interaction between two opposing forces: fitness differences between species, which should drive the best-adapted species to exclude others within a particular ecological niche, and stabilizing mechanisms, which maintains diversity via niche differentiation. For many species to be stabilized in a community, population growth must be negative density-dependent, i.e. all participating species have a tendency to increase in density as their populations decline. In such communities, any species that becomes rare will experience positive growth, pushing its population to recover and making local extinction unlikely. As the population of one species declines, individuals of that species tend to compete predominantly with individuals of other species. Thus, the tendency of a population to recover as it declines in density reflects reduced intraspecific competition (within-species) relative to interspecific competition (between-species), the signature of niche differentiation.
The Arditi–Ginzburg equations describe ratio-dependent predator–prey dynamics. Where N is the population of a prey species and P that of a predator, the population dynamics are described by the following two equations:
In theoretical ecology and nonlinear dynamics, consumer-resource models (CRMs) are a class of ecological models in which a community of consumer species compete for a common pool of resources. Instead of species interacting directly, all species-species interactions are mediated through resource dynamics. Consumer-resource models have served as fundamental tools in the quantitative development of theories of niche construction, coexistence, and biological diversity. These models can be interpreted as a quantitative description of a single trophic level.
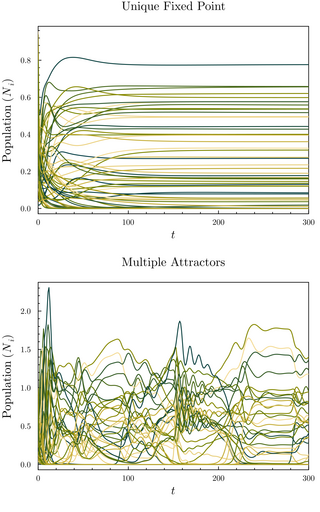
The random generalized Lotka–Volterra model (rGLV) is an ecological model and random set of coupled ordinary differential equations where the parameters of the generalized Lotka–Volterra equation are sampled from a probability distribution, analogously to quenched disorder. The rGLV models dynamics of a community of species in which each species' abundance grows towards a carrying capacity but is depleted due to competition from the presence of other species. It is often analyzed in the many-species limit using tools from statistical physics, in particular from spin glass theory.











