
In mathematical physics and mathematics, the Pauli matrices are a set of three 2 × 2 complex matrices that are Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma, they are occasionally denoted by tau when used in connection with isospin symmetries.

The uncertainty principle, also known as Heisenberg's indeterminacy principle, is a fundamental concept in quantum mechanics. It states that there is a limit to the precision with which certain pairs of physical properties, such as position and momentum, can be simultaneously known. In other words, the more accurately one property is measured, the less accurately the other property can be known.
In quantum field theory, the Dirac spinor is the spinor that describes all known fundamental particles that are fermions, with the possible exception of neutrinos. It appears in the plane-wave solution to the Dirac equation, and is a certain combination of two Weyl spinors, specifically, a bispinor that transforms "spinorially" under the action of the Lorentz group.
In quantum mechanics, a Slater determinant is an expression that describes the wave function of a multi-fermionic system. It satisfies anti-symmetry requirements, and consequently the Pauli principle, by changing sign upon exchange of two electrons. Only a small subset of all possible fermionic wave functions can be written as a single Slater determinant, but those form an important and useful subset because of their simplicity.
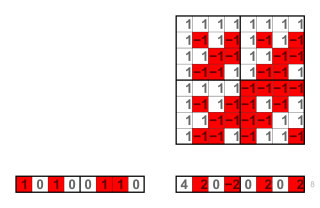
The Hadamard transform is an example of a generalized class of Fourier transforms. It performs an orthogonal, symmetric, involutive, linear operation on 2m real numbers.
In quantum computing and specifically the quantum circuit model of computation, a quantum logic gate is a basic quantum circuit operating on a small number of qubits. Quantum logic gates are the building blocks of quantum circuits, like classical logic gates are for conventional digital circuits.

The Stokes parameters are a set of values that describe the polarization state of electromagnetic radiation. They were defined by George Gabriel Stokes in 1852, as a mathematically convenient alternative to the more common description of incoherent or partially polarized radiation in terms of its total intensity (I), (fractional) degree of polarization (p), and the shape parameters of the polarization ellipse. The effect of an optical system on the polarization of light can be determined by constructing the Stokes vector for the input light and applying Mueller calculus, to obtain the Stokes vector of the light leaving the system. The original Stokes paper was discovered independently by Francis Perrin in 1942 and by Subrahamanyan Chandrasekhar in 1947, who named it as the Stokes parameters.
In physics, the Majorana equation is a relativistic wave equation. It is named after the Italian physicist Ettore Majorana, who proposed it in 1937 as a means of describing fermions that are their own antiparticle. Particles corresponding to this equation are termed Majorana particles, although that term now has a more expansive meaning, referring to any fermionic particle that is its own anti-particle.
In quantum mechanics, spin is an intrinsic property of all elementary particles. All known fermions, the particles that constitute ordinary matter, have a spin of 1/2. The spin number describes how many symmetrical facets a particle has in one full rotation; a spin of 1/2 means that the particle must be rotated by two full turns before it has the same configuration as when it started.
In quantum mechanics, eigenspinors are thought of as basis vectors representing the general spin state of a particle. Strictly speaking, they are not vectors at all, but in fact spinors. For a single spin 1/2 particle, they can be defined as the eigenvectors of the Pauli matrices.
In mathematics and physics, in particular quantum information, the term generalized Pauli matrices refers to families of matrices which generalize the properties of the Pauli matrices. Here, a few classes of such matrices are summarized.
The Steane code is a tool in quantum error correction introduced by Andrew Steane in 1996. It is a CSS code (Calderbank-Shor-Steane), using the classical binary [7,4,3] Hamming code to correct for qubit flip errors and the dual of the Hamming code, the [7,3,4] code, to correct for phase flip errors. The Steane code encodes one logical qubit in 7 physical qubits and is able to correct arbitrary single qubit errors.
The time-evolving block decimation (TEBD) algorithm is a numerical scheme used to simulate one-dimensional quantum many-body systems, characterized by at most nearest-neighbour interactions. It is dubbed Time-evolving Block Decimation because it dynamically identifies the relevant low-dimensional Hilbert subspaces of an exponentially larger original Hilbert space. The algorithm, based on the Matrix Product States formalism, is highly efficient when the amount of entanglement in the system is limited, a requirement fulfilled by a large class of quantum many-body systems in one dimension.
In quantum mechanics, the Pauli equation or Schrödinger–Pauli equation is the formulation of the Schrödinger equation for spin-½ particles, which takes into account the interaction of the particle's spin with an external electromagnetic field. It is the non-relativistic limit of the Dirac equation and can be used where particles are moving at speeds much less than the speed of light, so that relativistic effects can be neglected. It was formulated by Wolfgang Pauli in 1927. In its linearized form it is known as Lévy-Leblond equation.
In quantum mechanics, a raising or lowering operator is an operator that increases or decreases the eigenvalue of another operator. In quantum mechanics, the raising operator is sometimes called the creation operator, and the lowering operator the annihilation operator. Well-known applications of ladder operators in quantum mechanics are in the formalisms of the quantum harmonic oscillator and angular momentum.
In physics, and specifically in quantum field theory, a bispinor is a mathematical construction that is used to describe some of the fundamental particles of nature, including quarks and electrons. It is a specific embodiment of a spinor, specifically constructed so that it is consistent with the requirements of special relativity. Bispinors transform in a certain "spinorial" fashion under the action of the Lorentz group, which describes the symmetries of Minkowski spacetime. They occur in the relativistic spin-1/2 wave function solutions to the Dirac equation.
Spin is an intrinsic form of angular momentum carried by elementary particles, and thus by composite particles such as hadrons, atomic nuclei, and atoms. Spin is quantized, and accurate models for the interaction with spin require relativistic quantum mechanics or quantum field theory.
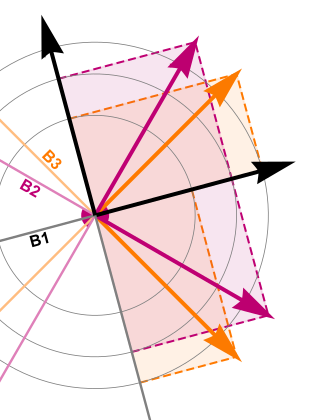
In quantum information theory, a set of bases in Hilbert space Cd are said to be mutually unbiased to mean, that, if a system is prepared in an eigenstate of one of the bases, then all outcomes of the measurement with respect to the other basis are predicted to occur with an equal probability inexorably equal to 1/d.
In quantum computing, the quantum Fourier transform (QFT) is a linear transformation on quantum bits, and is the quantum analogue of the discrete Fourier transform. The quantum Fourier transform is a part of many quantum algorithms, notably Shor's algorithm for factoring and computing the discrete logarithm, the quantum phase estimation algorithm for estimating the eigenvalues of a unitary operator, and algorithms for the hidden subgroup problem. The quantum Fourier transform was discovered by Don Coppersmith.
In quantum computing and quantum information theory, the Clifford gates are the elements of the Clifford group, a set of mathematical transformations which normalize the n-qubit Pauli group, i.e., map tensor products of Pauli matrices to tensor products of Pauli matrices through conjugation. The notion was introduced by Daniel Gottesman and is named after the mathematician William Kingdon Clifford. Quantum circuits that consist of only Clifford gates can be efficiently simulated with a classical computer due to the Gottesman–Knill theorem.



























