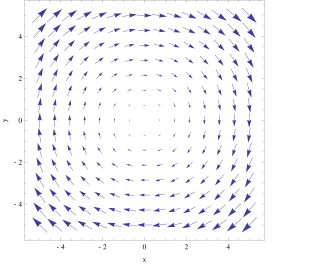
In vector calculus, the curl, also known as rotor, is a vector operator that describes the infinitesimal circulation of a vector field in three-dimensional Euclidean space. The curl at a point in the field is represented by a vector whose length and direction denote the magnitude and axis of the maximum circulation. The curl of a field is formally defined as the circulation density at each point of the field.
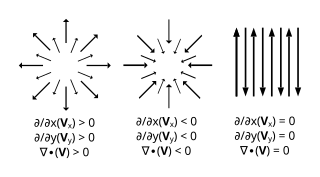
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the quantity of the vector field's source at each point. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around a given point.
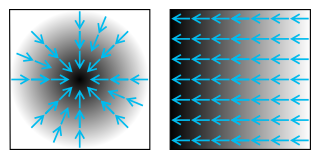
In vector calculus, the gradient of a scalar-valued differentiable function of several variables is the vector field whose value at a point gives the direction and the rate of fastest increase. The gradient transforms like a vector under change of basis of the space of variables of . If the gradient of a function is non-zero at a point , the direction of the gradient is the direction in which the function increases most quickly from , and the magnitude of the gradient is the rate of increase in that direction, the greatest absolute directional derivative. Further, a point where the gradient is the zero vector is known as a stationary point. The gradient thus plays a fundamental role in optimization theory, where it is used to minimize a function by gradient descent. In coordinate-free terms, the gradient of a function may be defined by:
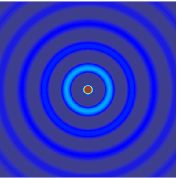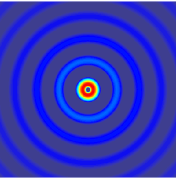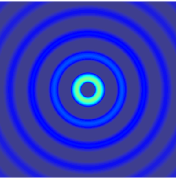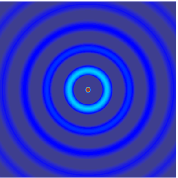
The wave equation is a second-order linear partial differential equation for the description of waves or standing wave fields such as mechanical waves or electromagnetic waves. It arises in fields like acoustics, electromagnetism, and fluid dynamics.
In physics, a conservative force is a force with the property that the total work done by the force in moving a particle between two points is independent of the path taken. Equivalently, if a particle travels in a closed loop, the total work done by a conservative force is zero.

In physics, work is the energy transferred to or from an object via the application of force along a displacement. In its simplest form, for a constant force aligned with the direction of motion, the work equals the product of the force strength and the distance traveled. A force is said to do positive work if when applied it has a component in the direction of the displacement of the point of application. A force does negative work if it has a component opposite to the direction of the displacement at the point of application of the force.
Del, or nabla, is an operator used in mathematics as a vector differential operator, usually represented by the nabla symbol ∇. When applied to a function defined on a one-dimensional domain, it denotes the standard derivative of the function as defined in calculus. When applied to a field, it may denote any one of three operations depending on the way it is applied: the gradient or (locally) steepest slope of a scalar field ; the divergence of a vector field; or the curl (rotation) of a vector field.
In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols , (where is the nabla operator), or . In a Cartesian coordinate system, the Laplacian is given by the sum of second partial derivatives of the function with respect to each independent variable. In other coordinate systems, such as cylindrical and spherical coordinates, the Laplacian also has a useful form. Informally, the Laplacian Δf (p) of a function f at a point p measures by how much the average value of f over small spheres or balls centered at p deviates from f (p).

In fluid dynamics, two types of stream function are defined:

In mathematics, a Green's function is the impulse response of an inhomogeneous linear differential operator defined on a domain with specified initial conditions or boundary conditions.
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given by a principal connection on the frame bundle – see affine connection. In the special case of a manifold isometrically embedded into a higher-dimensional Euclidean space, the covariant derivative can be viewed as the orthogonal projection of the Euclidean directional derivative onto the manifold's tangent space. In this case the Euclidean derivative is broken into two parts, the extrinsic normal component and the intrinsic covariant derivative component.

In mathematical physics, scalar potential, simply stated, describes the situation where the difference in the potential energies of an object in two different positions depends only on the positions, not upon the path taken by the object in traveling from one position to the other. It is a scalar field in three-space: a directionless value (scalar) that depends only on its location. A familiar example is potential energy due to gravity.
A directional derivative is a concept in multivariable calculus that measures the rate at which a function changes in a particular direction at a given point.
In differential geometry, the four-gradient is the four-vector analogue of the gradient from vector calculus.
In physics, a force field is a vector field corresponding with a non-contact force acting on a particle at various positions in space. Specifically, a force field is a vector field , where is the force that a particle would feel if it were at the point .

In geometry, a three-dimensional space is a mathematical space in which three values (coordinates) are required to determine the position of a point. Most commonly, it is the three-dimensional Euclidean space, that is, the Euclidean space of dimension three, which models physical space. More general three-dimensional spaces are called 3-manifolds. The term may also refer colloquially to a subset of space, a three-dimensional region, a solid figure.
In mathematical physics, spacetime algebra (STA) is the application of Clifford algebra Cl1,3(R), or equivalently the geometric algebra G(M4) to physics. Spacetime algebra provides a "unified, coordinate-free formulation for all of relativistic physics, including the Dirac equation, Maxwell equation and General Relativity" and "reduces the mathematical divide between classical, quantum and relativistic physics."
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve. The terms path integral, curve integral, and curvilinear integral are also used; contour integral is used as well, although that is typically reserved for line integrals in the complex plane.
In physics, a sinusoidal plane wave is a special case of plane wave: a field whose value varies as a sinusoidal function of time and of the distance from some fixed plane. It is also called a monochromatic plane wave, with constant frequency.

In mathematics and physics, a traveling plane wave is a special case of plane wave, namely a field whose evolution in time can be described as simple translation of its values at a constant wave speed, along a fixed direction of propagation.







































