In geometry, a partition of a polygon is a set of primitive units (e.g. squares), which do not overlap and whose union equals the polygon. A polygon partition problem is a problem of finding a partition which is minimal in some sense, for example a partition with a smallest number of units or with units of smallest total side-length.
Polygon partitioning is an important class of problems in computational geometry. There are many different polygon partition problems, depending on the type of polygon being partitioned and on the types of units allowed in the partition.
The term polygon decomposition is often used as a general term that includes both polygon covering and partitioning. [1]
Polygon decomposition is applied in several areas: [1]
The most well-studied polygon partition problem is partitioning to a smallest number of triangles, also called triangulation. For a hole-free polygon with vertices, a triangulation can be calculated in time . For a polygon with holes, there is a lower bound of .
A related problem is partitioning to triangles with a minimal total edge length, also called minimum-weight triangulation.
The same two variants of the problem were studied for the case in which the pieces should be pseudotriangles – polygons that like triangles have exactly three convex vertices. The variants are: partitioning to a smallest number of pseodutriangles, and partitioning to pseudotriangles with a minimal total edge length.
A special sub-family of polygon partition problems arises when the large polygon is a rectilinear polygon (also called: orthogonal polygon). In this case, the most important component shape to consider is the rectangle. [1]
Rectangular partitions have many applications. In VLSI design, it is necessary to decompose masks into the simpler shapes available in lithographic pattern generators, and similar mask decomposition problems also arise in DNA microarray design. Rectangular partitions can simplify convolution operations in image processing and can be used to compress bitmap images. Closely related matrix decomposition problems have been applied to radiation therapy planning, and rectangular partitions have also been used to design robot self-assembly sequences. [2]
The problem of minimizing the number of component rectangles is polynomial: several polynomial-time algorithms are known. See [1] : 10–13 and [2] : 3–5 for surveys.
The problem of partitioning a rectilinear polygon to a smallest number of squares (in contrast to arbitrary rectangles) is NP-hard. [3]
In some applications, it is more important to minimize the total length of the cuts (e.g. to minimize the cost of performing the partition, or to minimize the amount of dust). This problem is called minimum edge-length rectangular partitioning. It was first studied by Lingas, Pinter, Rivest and Shamir in 1982. [4] [5] The run-time complexity of this problem crucially depends on whether the raw polygon is allowed to have holes.
If the raw polygon is hole-free, then an optimal partition can be found in time , where n is the number of vertices of the polygon. In the special case of a "histogram polygon", the complexity improves to . [4] The algorithm uses dynamic programming and relies on the following fact: if the polygon is hole-free, then it has a minimum-length partition in which each maximal line-segment contains a vertex of the boundary. The reason is that, in any minimum-length partition, every maximal line-segment can be "pushed" until it hits one of the vertices of the boundary, without changing the total length. Therefore, there are only candidates for a line segment in an optimal partition, and they can be checked efficiently using dynamic programming. [5] : 166–167
If the raw polygon might have holes, even if they are degenerate holes (i.e., single points), the problem is NP-hard. This can be proved by reduction from Planar SAT. [4] [6] For the case in which all holes are single points, several constant-factor approximations have been developed:
In this setting, the large polygon already contains some pairwise-disjoint rectangles. The goal is to find a partition of the polygon into rectangles such that each original rectangle is contained in one of the pieces, and subject to this, the number of "blanks" (pieces that do not contain an original rectangle) is as small as possible. The following results are known: [12]
In VLSI artwork processing systems, it is often required to partition a polygonal region into the minimum number of trapezoids, with two horizontal sides. A triangle with a horizontal side is considered to be a trapezoid with two horizontal sides one of which is degenerate. For a hole-free polygon with sides, a smallest such partition can be found in time . [13]
If the number of trapezoids need not be minimal a trapezoidation can be found in time , as a by-product of a polygon triangulation algorithm. [14]
If the polygon does contain holes, the problem is NP-complete, but a 3-approximation can be found in time . [13]
A quadrilateralization or a quadrangulation is a partition into quadrilaterals.
A recurring characteristic of quadrangulation problems is whether they Steiner point are allowed, i.e., whether the algorithm is allowed to add points which are not vertices of the polygon. Allowing Steiner points may enable smaller divisions, but then it is much more difficult to guarantee that the divisions found by an algorithms have minimum size.
There are linear-time algorithms for quadrangulations of hole-free polygons with Steiner points, but they are not guaranteed to find a smallest partition. [15] [16]
A generalization of previous problems is the partitioning into polygons that have exactly m sides, or at most m sides. Here the goal is to minimize the total edge length. This problem can be solved in time polynomial in n and m. [17] [18]
When partitioning a general polygon into convex polygons, several objectives have been studied.
The optimal convex partitioning problem is to partition a non-convex polygon into as few as possible convex polygons, using only the initial polygon's vertices. There are exact and approximate algorithms for this problem. [19]
The original polygon already contains some pairwise-disjoint convex figures, and the goal is to partition it into convex polygons that such that each original figure is contained in one of the pieces, and subject to this, the number of "blanks" (pieces that do not contain an original figure) is as small as possible. If the large polygon is convex, then in any maximal arrangement of n convex figures, all the holes are convex, and their number is at most , and this is tight. [12]
The fair polygon partitioning problem [20] is to partition a (convex) polygon into (convex) pieces with an equal perimeter and equal area (this is a special case of fair cake-cutting). Any convex polygon can be easily cut into any number n of convex pieces with an area of exactly 1/n. However, ensuring that the pieces have both equal area and equal perimeter is more challenging. There are algorithms for solving this problem when the number of pieces is a power of 2. [21]
A generalization of this problem is when the area and perimeter measures are replaced with a measure on the body and on the boundary of the polygon, respectively. This problem was studied for 2 and 3 pieces. [22]
There is a further generalization to handle any number of measures.
More general shapes of pieces have been studied, including: spiral shapes, star polygons and monotone polygons. See [1] for a survey.
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational geometry. While modern computational geometry is a recent development, it is one of the oldest fields of computing with a history stretching back to antiquity.
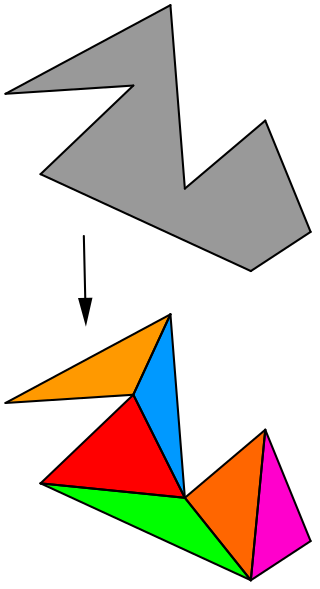
In computational geometry, polygon triangulation is the partition of a polygonal area P into a set of triangles, i.e., finding a set of triangles with pairwise non-intersecting interiors whose union is P.
A Euclidean minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space connects the points by a system of line segments with the points as endpoints, minimizing the total length of the segments. In it, any two points can reach each other along a path through the line segments. It can be found as the minimum spanning tree of a complete graph with the points as vertices and the Euclidean distances between points as edge weights.
In geometry, a simple polygon is a polygon that does not intersect itself and has no holes. That is, they are piecewise-linear Jordan curves consisting of finitely many line segments. They include as special cases the convex polygons, star-shaped polygons, and monotone polygons.
A triangulation of a set of points in the Euclidean space is a simplicial complex that covers the convex hull of , and whose vertices belong to . In the plane, triangulations are made up of triangles, together with their edges and vertices. Some authors require that all the points of are vertices of its triangulations. In this case, a triangulation of a set of points in the plane can alternatively be defined as a maximal set of non-crossing edges between points of . In the plane, triangulations are special cases of planar straight-line graphs.
In geometry, a triangulation is a subdivision of a planar object into triangles, and by extension the subdivision of a higher-dimension geometric object into simplices. Triangulations of a three-dimensional volume would involve subdividing it into tetrahedra packed together.
The art gallery problem or museum problem is a well-studied visibility problem in computational geometry. It originates from the following real-world problem:
Matrix chain multiplication is an optimization problem concerning the most efficient way to multiply a given sequence of matrices. The problem is not actually to perform the multiplications, but merely to decide the sequence of the matrix multiplications involved. The problem may be solved using dynamic programming.
Guillotine cutting is the process of producing small rectangular items of fixed dimensions from a given large rectangular sheet, using only guillotine-cuts. A guillotine-cut is a straight bisecting line going from one edge of an existing rectangle to the opposite edge, similarly to a paper guillotine.
A rectilinear polygon is a polygon all of whose sides meet at right angles. Thus the interior angle at each vertex is either 90° or 270°. Rectilinear polygons are a special case of isothetic polygons.
In Euclidean plane geometry, a pseudotriangle (pseudo-triangle) is the simply connected subset of the plane that lies between any three mutually tangent convex sets. A pseudotriangulation (pseudo-triangulations) is a partition of a region of the plane into pseudotriangles, and a pointed pseudotriangulation is a pseudotriangulation in which at each vertex the incident edges span an angle of less than π.
Algorithms that construct convex hulls of various objects have a broad range of applications in mathematics and computer science.
A geometric spanner or a t-spanner graph or a t-spanner was initially introduced as a weighted graph over a set of points as its vertices for which there is a t-path between any pair of vertices for a fixed parameter t. A t-path is defined as a path through the graph with weight at most t times the spatial distance between its endpoints. The parameter t is called the stretch factor or dilation factor of the spanner.
In computational geometry, the smallest enclosing box problem is that of finding the oriented minimum bounding box enclosing a set of points. It is a type of bounding volume. "Smallest" may refer to volume, area, perimeter, etc. of the box.
In computational geometry, the method of rotating calipers is an algorithm design technique that can be used to solve optimization problems including finding the width or diameter of a set of points.
In computational geometry and computer science, the minimum-weight triangulation problem is the problem of finding a triangulation of minimal total edge length. That is, an input polygon or the convex hull of an input point set must be subdivided into triangles that meet edge-to-edge and vertex-to-vertex, in such a way as to minimize the sum of the perimeters of the triangles. The problem is NP-hard for point set inputs, but may be approximated to any desired degree of accuracy. For polygon inputs, it may be solved exactly in polynomial time. The minimum weight triangulation has also sometimes been called the optimal triangulation.
In discrete geometry, an opaque set is a system of curves or other set in the plane that blocks all lines of sight across a polygon, circle, or other shape. Opaque sets have also been called barriers, beam detectors, opaque covers, or opaque forests. Opaque sets were introduced by Stefan Mazurkiewicz in 1916, and the problem of minimizing their total length was posed by Frederick Bagemihl in 1959.
In geometry, a covering of a polygon is a set of primitive units whose union equals the polygon. A polygon covering problem is a problem of finding a covering with a smallest number of units for a given polygon. This is an important class of problems in computational geometry. There are many different polygon covering problems, depending on the type of polygon being covered. An example polygon covering problem is: given a rectilinear polygon, find a smallest set of squares whose union equals the polygon.
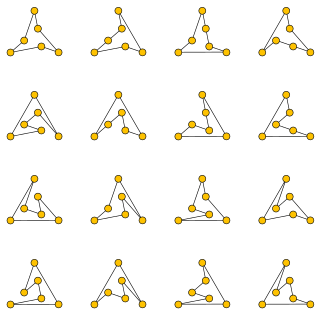
In computational geometry, a polygonalization of a finite set of points in the Euclidean plane is a simple polygon with the given points as its vertices. A polygonalization may also be called a polygonization, simple polygonalization, Hamiltonian polygon, non-crossing Hamiltonian cycle, or crossing-free straight-edge spanning cycle.
Guillotine partition is the process of partitioning a rectilinear polygon, possibly containing some holes, into rectangles, using only guillotine-cuts. A guillotine-cut is a straight bisecting line going from one edge of an existing polygon to the opposite edge, similarly to a paper guillotine.
