Polygon triangulation

Last updated
Polygon triangulation Trianguliatsiia.svg
Polygon triangulation

In computational geometry, polygon triangulation is the partition of a polygonal area (simple polygon) P into a set of triangles, [1] i.e., finding a set of triangles with pairwise non-intersecting interiors whose union is P.

Contents

Triangulations may be viewed as special cases of planar straight-line graphs. When there are no holes or added points, triangulations form maximal outerplanar graphs.

Polygon triangulation without extra vertices

Over time, a number of algorithms have been proposed to triangulate a polygon.

Special cases

The 42 possible triangulations for a convex heptagon (7-sided convex polygon). This number is given by the 5th Catalan number. Polygon Triangulations (heptagon).svg
The 42 possible triangulations for a convex heptagon (7-sided convex polygon). This number is given by the 5th Catalan number.

It is trivial to triangulate any convex polygon in linear time into a fan triangulation, by adding diagonals from one vertex to all other non-nearest neighbor vertices.

The total number of ways to triangulate a convex n-gon by non-intersecting diagonals is the (n−2)nd Catalan number, which equals

,

a formula found by Leonhard Euler. [2]

A monotone polygon can be triangulated in linear time with either the algorithm of A. Fournier and D.Y. Montuno, [3] or the algorithm of Godfried Toussaint. [4]

Ear clipping method

A polygon ear Polygon-ear.png
A polygon ear

One way to triangulate a simple polygon is based on the two ears theorem, as the fact that any simple polygon with at least 4 vertices without holes has at least two "ears", which are triangles with two sides being the edges of the polygon and the third one completely inside it. [5] The algorithm then consists of finding such an ear, removing it from the polygon (which results in a new polygon that still meets the conditions) and repeating until there is only one triangle left.

This algorithm is easy to implement, but slower than some other algorithms, and it only works on polygons without holes. An implementation that keeps separate lists of convex and concave vertices will run in O(n2) time. This method is known as ear clipping and sometimes ear trimming. An efficient algorithm for cutting off ears was discovered by Hossam ElGindy, Hazel Everett, and Godfried Toussaint. [6]

Monotone polygon triangulation

Breaking a polygon into monotone polygons Polygon-to-monotone.png
Breaking a polygon into monotone polygons

A simple polygon is monotone with respect to a line L, if any line orthogonal to L intersects the polygon at most twice. A monotone polygon can be split into two monotone chains. A polygon that is monotone with respect to the y-axis is called y-monotone. A monotone polygon with n vertices can be triangulated in O(n) time. Assuming a given polygon is y-monotone, the greedy algorithm begins by walking on one chain of the polygon from top to bottom while adding diagonals whenever it is possible. [1] It is easy to see that the algorithm can be applied to any monotone polygon.

Triangulating a non-monotone polygon

If a polygon is not monotone, it can be partitioned into monotone subpolygons in O(n log n) time using a sweep-line approach. The algorithm does not require the polygon to be simple, thus it can be applied to polygons with holes. Generally, this algorithm can triangulate a planar subdivision with n vertices in O(n log n) time using O(n) space. [1]

Dual graph of a triangulation

A useful graph that is often associated with a triangulation of a polygon P is the dual graph. Given a triangulation TP of P, one defines the graph G(TP) as the graph whose vertex set are the triangles of TP, two vertices (triangles) being adjacent if and only if they share a diagonal. It is easy to observe that G(TP) is a tree with maximum degree 3.

Computational complexity

Until 1988, whether a simple polygon can be triangulated faster than O(n log n) time was an open problem in computational geometry. [1] Then, Tarjan & Van Wyk (1988) discovered an O(n log log n)-time algorithm for triangulation, [7] later simplified by Kirkpatrick, Klawe & Tarjan (1992). [8] Several improved methods with complexity O(n log*n) (in practice, indistinguishable from linear time) followed. [9] [10] [11]

Bernard Chazelle showed in 1991 that any simple polygon can be triangulated in linear time, though the proposed algorithm is very complex. [12] A simpler randomized algorithm with linear expected time is also known. [13]

Seidel's decomposition algorithm [10] and Chazelle's triangulation method are discussed in detail in Li & Klette (2011). [14]

The time complexity of triangulation of an n-vertex polygon with holes has an Ω(n log n) lower bound, in algebraic computation tree models of computation. [1] It is possible to compute the number of distinct triangulations of a simple polygon in polynomial time using dynamic programming, and (based on this counting algorithm) to generate uniformly random triangulations in polynomial time. [15] However, counting the triangulations of a polygon with holes is #P-complete, making it unlikely that it can be done in polynomial time. [16]

See also

Related Research Articles

<span class="mw-page-title-main">Delaunay triangulation</span> Triangulation method

In computational geometry, a Delaunay triangulation or Delone triangulation of a set of points in the plane subdivides their convex hull into triangles whose circumcircles do not contain any of the points. This maximizes the size of the smallest angle in any of the triangles, and tends to avoid sliver triangles.

The point location problem is a fundamental topic of computational geometry. It finds applications in areas that deal with processing geometrical data: computer graphics, geographic information systems (GIS), motion planning, and computer aided design (CAD).

<span class="mw-page-title-main">Simple polygon</span> Shape bounded by non-intersecting line segments

In geometry, a simple polygon is a polygon that does not intersect itself and has no holes. That is, it is a piecewise-linear Jordan curve consisting of finitely many line segments. These polygons include as special cases the convex polygons, star-shaped polygons, and monotone polygons.

<span class="mw-page-title-main">Point-set triangulation</span> Simplicial complex in Euclidean geometry

A triangulation of a set of points in the Euclidean space is a simplicial complex that covers the convex hull of , and whose vertices belong to . In the plane, triangulations are made up of triangles, together with their edges and vertices. Some authors require that all the points of are vertices of its triangulations. In this case, a triangulation of a set of points in the plane can alternatively be defined as a maximal set of non-crossing edges between points of . In the plane, triangulations are special cases of planar straight-line graphs.

The art gallery problem or museum problem is a well-studied visibility problem in computational geometry. It originates from the following real-world problem:

"In an art gallery, what is the minimum number of guards who together can observe the whole gallery?"

<span class="mw-page-title-main">Straight skeleton</span> Method in geometry for representing a polygon by a topological skeleton

In geometry, a straight skeleton is a method of representing a polygon by a topological skeleton. It is similar in some ways to the medial axis but differs in that the skeleton is composed of straight line segments, while the medial axis of a polygon may involve parabolic curves. However, both are homotopy-equivalent to the underlying polygon.

<span class="mw-page-title-main">Pseudotriangle</span>

In Euclidean plane geometry, a pseudotriangle (pseudo-triangle) is the simply connected subset of the plane that lies between any three mutually tangent convex sets. A pseudotriangulation (pseudo-triangulations) is a partition of a region of the plane into pseudotriangles, and a pointed pseudotriangulation is a pseudotriangulation in which at each vertex the incident edges span an angle of less than π.

In computational geometry, the Bowyer–Watson algorithm is a method for computing the Delaunay triangulation of a finite set of points in any number of dimensions. The algorithm can be also used to obtain a Voronoi diagram of the points, which is the dual graph of the Delaunay triangulation.

Algorithms that construct convex hulls of various objects have a broad range of applications in mathematics and computer science.

<span class="mw-page-title-main">Monotone polygon</span>

In geometry, a polygon P in the plane is called monotone with respect to a straight line L, if every line orthogonal to L intersects the boundary of P at most twice.

<span class="mw-page-title-main">Rotating calipers</span>

In computational geometry, the method of rotating calipers is an algorithm design technique that can be used to solve optimization problems including finding the width or diameter of a set of points.

In computational geometry and computer science, the minimum-weight triangulation problem is the problem of finding a triangulation of minimal total edge length. That is, an input polygon or the convex hull of an input point set must be subdivided into triangles that meet edge-to-edge and vertex-to-vertex, in such a way as to minimize the sum of the perimeters of the triangles. The problem is NP-hard for point set inputs, but may be approximated to any desired degree of accuracy. For polygon inputs, it may be solved exactly in polynomial time. The minimum weight triangulation has also sometimes been called the optimal triangulation.

In computational geometry, a constrained Delaunay triangulation is a generalization of the Delaunay triangulation that forces certain required segments into the triangulation as edges, unlike the Delaunay triangulation itself which is based purely on the position of a given set of vertices without regard to how they should be connected by edges. It can be computed efficiently and has applications in geographic information systems and in mesh generation.

In geometry, a covering of a polygon is a set of primitive units whose union equals the polygon. A polygon covering problem is a problem of finding a covering with a smallest number of units for a given polygon. This is an important class of problems in computational geometry. There are many different polygon covering problems, depending on the type of polygon being covered. An example polygon covering problem is: given a rectilinear polygon, find a smallest set of squares whose union equals the polygon.

In geometry, a partition of a polygon is a set of primitive units, which do not overlap and whose union equals the polygon. A polygon partition problem is a problem of finding a partition which is minimal in some sense, for example a partition with a smallest number of units or with units of smallest total side-length.

<span class="mw-page-title-main">Two ears theorem</span> Every simple polygon with more than three vertices has at least two ears

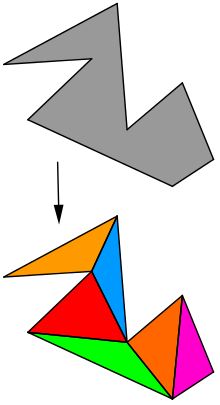
In geometry, the two ears theorem states that every simple polygon with more than three vertices has at least two ears, vertices that can be removed from the polygon without introducing any crossings. The two ears theorem is equivalent to the existence of polygon triangulations. It is frequently attributed to Gary H. Meisters, but was proved earlier by Max Dehn.

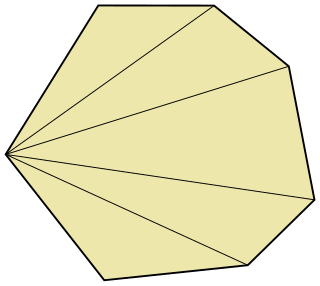
<span class="mw-page-title-main">Fan triangulation</span> Method of triangulating complex polygons

In computational geometry, a fan triangulation is a simple way to triangulate a polygon by choosing a vertex and drawing edges to all of the other vertices of the polygon. Not every polygon can be triangulated this way, so this method is usually only used for convex polygons.

<span class="mw-page-title-main">Relative convex hull</span>

In discrete geometry and computational geometry, the relative convex hull or geodesic convex hull is an analogue of the convex hull for the points inside a simple polygon or a rectifiable simple closed curve.

<span class="mw-page-title-main">Polygonalization</span> Polygon through a set of points

In computational geometry, a polygonalization of a finite set of points in the Euclidean plane is a simple polygon with the given points as its vertices. A polygonalization may also be called a polygonization, simple polygonalization, Hamiltonian polygon, non-crossing Hamiltonian cycle, or crossing-free straight-edge spanning cycle.

In discrete mathematics and theoretical computer science, the flip distance between two triangulations of the same point set is the number of flips required to transform one triangulation into another. A flip removes an edge between two triangles in the triangulation and then adds the other diagonal in the edge's enclosing quadrilateral, forming a different triangulation of the same point set.

References

  1. 1 2 3 4 5 Mark de Berg, Marc van Kreveld, Mark Overmars, and Otfried Schwarzkopf (2000), "3: Polygon Triangulation", Computational Geometry (2nd ed.), Springer-Verlag, pp. 45–61, ISBN   3-540-65620-0 {{citation}}: CS1 maint: multiple names: authors list (link)
  2. ↑ Pickover, Clifford A. (2009), The Math Book, Sterling, p. 184
  3. ↑ Fournier, Alain; Montuno, Delfin Y. (1984), "Triangulating simple polygons and equivalent problems", ACM Transactions on Graphics , 3 (2): 153–174, doi: 10.1145/357337.357341 , ISSN   0730-0301, S2CID   33344266
  4. ↑ Toussaint, Godfried T. (1984), "A new linear algorithm for triangulating monotone polygons", Pattern Recognition Letters, 2 (3): 155–158, Bibcode:1984PaReL...2..155T, doi:10.1016/0167-8655(84)90039-4
  5. ↑ Meisters, Gary Hosler (1975), "Polygons have ears", American Mathematical Monthly , 82 (6): 648–651, doi:10.2307/2319703, JSTOR   2319703
  6. ↑ ElGindy, Hossam; Everett, Hazel; Toussaint, Godfried T. (1993), "Slicing an ear using prune-and-search", Pattern Recognition Letters, 14 (9): 719–722, Bibcode:1993PaReL..14..719E, doi:10.1016/0167-8655(93)90141-y
  7. ↑ Tarjan, Robert E.; Van Wyk, Christopher J. (1988), "An O(n log log n)-time algorithm for triangulating a simple polygon", SIAM Journal on Computing , 17 (1): 143–178, CiteSeerX   10.1.1.186.5949 , doi:10.1137/0217010, MR   0925194
  8. ↑ Kirkpatrick, David G.; Klawe, Maria M.; Tarjan, Robert E. (1992), "Polygon triangulation in O(n log log n) time with simple data structures", Discrete & Computational Geometry , 7 (4): 329–346, doi: 10.1007/BF02187846 , MR   1148949
  9. ↑ Clarkson, Kenneth L.; Tarjan, Robert; van Wyk, Christopher J. (1989), "A fast Las Vegas algorithm for triangulating a simple polygon", Discrete & Computational Geometry , 4 (5): 423–432, doi: 10.1007/BF02187741
  10. 1 2 Seidel, Raimund (1991), "A Simple and Fast Incremental Randomized Algorithm for Computing Trapezoidal Decompositions and for Triangulating Polygons", Computational Geometry , 1: 51–64, CiteSeerX   10.1.1.55.5877 , doi: 10.1016/0925-7721(91)90012-4
  11. ↑ Clarkson, Kenneth L.; Cole, Richard; Tarjan, Robert E. (1992), "Randomized parallel algorithms for trapezoidal diagrams", International Journal of Computational Geometry & Applications, 2 (2): 117–133, doi:10.1142/S0218195992000081, MR   1168952
  12. ↑ Chazelle, Bernard (1991), "Triangulating a Simple Polygon in Linear Time", Discrete & Computational Geometry , 6 (3): 485–524, doi: 10.1007/BF02574703 , ISSN   0179-5376
  13. ↑ Amato, Nancy M.; Goodrich, Michael T.; Ramos, Edgar A. (2001), "A Randomized Algorithm for Triangulating a Simple Polygon in Linear Time", Discrete & Computational Geometry , 26 (2): 245–265, doi: 10.1007/s00454-001-0027-x , ISSN   0179-5376
  14. ↑ Li, Fajie; Klette, Reinhard (2011), Euclidean Shortest Paths, Springer, doi:10.1007/978-1-4471-2256-2, ISBN   978-1-4471-2255-5
  15. ↑ Epstein, Peter; Sack, Jörg-Rüdiger (1994), "Generating triangulations at random", ACM Transactions on Modeling and Computer Simulation, 4 (3): 267–278, doi:10.1145/189443.189446, S2CID   14039662
  16. ↑ Eppstein, David (2019), "Counting polygon triangulations is hard", Proc. 35nd Int. Symp. Computational Geometry, Leibniz International Proceedings in Informatics (LIPIcs), vol. 129, Schloss Dagstuhl, pp. 33:1–33:17, arXiv: 1903.04737 , doi:10.4230/LIPIcs.SoCG.2019.33, ISBN   9783959771047, S2CID   75136891
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.