
Surface tension is the tendency of liquid surfaces at rest to shrink into the minimum surface area possible. Surface tension is what allows objects with a higher density than water such as razor blades and insects to float on a water surface without becoming even partly submerged.

Sintering or frittage is the process of compacting and forming a solid mass of material by pressure or heat without melting it to the point of liquefaction. Sintering happens as part of a manufacturing process used with metals, ceramics, plastics, and other materials. The nanoparticles in the sintered material diffuse across the boundaries of the particles, fusing the particles together and creating a solid piece.
In thermodynamics, the chemical potential of a species is the energy that can be absorbed or released due to a change of the particle number of the given species, e.g. in a chemical reaction or phase transition. The chemical potential of a species in a mixture is defined as the rate of change of free energy of a thermodynamic system with respect to the change in the number of atoms or molecules of the species that are added to the system. Thus, it is the partial derivative of the free energy with respect to the amount of the species, all other species' concentrations in the mixture remaining constant. When both temperature and pressure are held constant, and the number of particles is expressed in moles, the chemical potential is the partial molar Gibbs free energy. At chemical equilibrium or in phase equilibrium, the total sum of the product of chemical potentials and stoichiometric coefficients is zero, as the free energy is at a minimum. In a system in diffusion equilibrium, the chemical potential of any chemical species is uniformly the same everywhere throughout the system.

In surface science, surface energy quantifies the disruption of intermolecular bonds that occurs when a surface is created. In solid-state physics, surfaces must be intrinsically less energetically favorable than the bulk of the material, otherwise there would be a driving force for surfaces to be created, removing the bulk of the material by sublimation. The surface energy may therefore be defined as the excess energy at the surface of a material compared to the bulk, or it is the work required to build an area of a particular surface. Another way to view the surface energy is to relate it to the work required to cut a bulk sample, creating two surfaces. There is "excess energy" as a result of the now-incomplete, unrealized bonding between the two created surfaces.

A granular material is a conglomeration of discrete solid, macroscopic particles characterized by a loss of energy whenever the particles interact. The constituents that compose granular material are large enough such that they are not subject to thermal motion fluctuations. Thus, the lower size limit for grains in granular material is about 1 μm. On the upper size limit, the physics of granular materials may be applied to ice floes where the individual grains are icebergs and to asteroid belts of the Solar System with individual grains being asteroids.

Wetting is the ability of a liquid to maintain contact with a solid surface, resulting from intermolecular interactions when the two are brought together. This happens in presence of a gaseous phase or another liquid phase not miscible with the first one. The degree of wetting (wettability) is determined by a force balance between adhesive and cohesive forces. There are two types of wetting: non-reactive wetting and reactive wetting.
In fluid mechanics, dewetting is one of the processes that can occur at a solid–liquid, solid–solid or liquid–liquid interface. Generally, dewetting describes the process of retraction of a fluid from a non-wettable surface it was forced to cover. The opposite process—spreading of a liquid on a substrate—is called wetting. The factor determining the spontaneous spreading and dewetting for a drop of liquid placed on a solid substrate with ambient gas, is the so-called spreading coefficient S:

The Marangoni effect is the mass transfer along an interface between two phases due to a gradient of the surface tension. In the case of temperature dependence, this phenomenon may be called thermo-capillary convection.

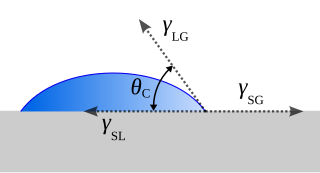
The contact angle is the angle between a liquid surface and a solid surface where they meet. More specifically, it is the angle between the surface tangent on the liquid–vapor interface and the tangent on the solid–liquid interface at their intersection. It quantifies the wettability of a solid surface by a liquid via the Young equation.

A Langmuir–Blodgett (LB) film is a nanostructured system formed when Langmuir films—or Langmuir monolayers (LM)—are transferred from the liquid-gas interface to solid supports during the vertical passage of the support through the monolayers. LB films can contain one or more monolayers of an organic material, deposited from the surface of a liquid onto a solid by immersing the solid substrate into the liquid. A monolayer is adsorbed homogeneously with each immersion or emersion step, thus films with very accurate thickness can be formed. This thickness is accurate because the thickness of each monolayer is known and can therefore be added to find the total thickness of a Langmuir–Blodgett film.
The Gibbs adsorption isotherm for multicomponent systems is an equation used to relate the changes in concentration of a component in contact with a surface with changes in the surface tension, which results in a corresponding change in surface energy. For a binary system, the Gibbs adsorption equation in terms of surface excess is:
The Kelvin equation describes the change in vapour pressure due to a curved liquid–vapor interface, such as the surface of a droplet. The vapor pressure at a convex curved surface is higher than that at a flat surface. The Kelvin equation is dependent upon thermodynamic principles and does not allude to special properties of materials. It is also used for determination of pore size distribution of a porous medium using adsorption porosimetry. The equation is named in honor of William Thomson, also known as Lord Kelvin.
The Marangoni number (Ma) is, as usually defined, the dimensionless number that compares the rate of transport due to Marangoni flows, with the rate of transport of diffusion. The Marangoni effect is flow of a liquid due to gradients in the surface tension of the liquid. Diffusion is of whatever is creating the gradient in the surface tension. Thus as the Marangoni number compares flow and diffusion timescales it is a type of Péclet number.
Melting-point depression is the phenomenon of reduction of the melting point of a material with a reduction of its size. This phenomenon is very prominent in nanoscale materials, which melt at temperatures hundreds of degrees lower than bulk materials.

The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water. Viscosity is defined scientifically as a force multiplied by a time divided by an area. Thus its SI units are newton-seconds per square meter, or pascal-seconds.
In surface chemistry, disjoining pressure according to an IUPAC definition arises from an attractive interaction between two surfaces. For two flat and parallel surfaces, the value of the disjoining pressure can be calculated as the derivative of the Gibbs energy of interaction per unit area in respect to distance. There is also a related concept of disjoining force, which can be viewed as disjoining pressure times the surface area of the interacting surfaces.
The Gibbs–Thomson effect, in common physics usage, refers to variations in vapor pressure or chemical potential across a curved surface or interface. The existence of a positive interfacial energy will increase the energy required to form small particles with high curvature, and these particles will exhibit an increased vapor pressure. See Ostwald–Freundlich equation. More specifically, the Gibbs–Thomson effect refers to the observation that small crystals are in equilibrium with their liquid melt at a lower temperature than large crystals. In cases of confined geometry, such as liquids contained within porous media, this leads to a depression in the freezing point / melting point that is inversely proportional to the pore size, as given by the Gibbs–Thomson equation.

Photolithography is a process in removing select portions of thin films used in microfabrication. Microfabrication is the production of parts on the micro- and nano- scale, typically on the surface of silicon wafers, for the production of integrated circuits, microelectromechanical systems (MEMS), solar cells, and other devices. Photolithography makes this process possible through the combined use of hexamethyldisilazane (HMDS), photoresist, spin coating, photomask, an exposure system and other various chemicals. By carefully manipulating these factors it is possible to create nearly any geometry microstructure on the surface of a silicon wafer. The chemical interaction between all the different components and the surface of the silicon wafer makes photolithography an interesting chemistry problem. Current engineering has been able to create features on the surface of silicon wafers between 1 and 100 μm.
In fluid mechanics, the thin-film equation is a partial differential equation that approximately predicts the time evolution of the thickness h of a liquid film that lies on a surface. The equation is derived via lubrication theory which is based on the assumption that the length-scales in the surface directions are significantly larger than in the direction normal to the surface. In the non-dimensional form of the Navier-Stokes equation the requirement is that terms of order ε2 and ε2Re are negligible, where ε ≪ 1 is the aspect ratio and Re is the Reynolds number. This significantly simplifies the governing equations. However, lubrication theory, as the name suggests, is typically derived for flow between two solid surfaces, hence the liquid forms a lubricating layer. The thin-film equation holds when there is a single free surface. With two free surfaces, the flow must be treated as a viscous sheet.
Liquid phase sintering is a sintering technique that uses a liquid phase to accelerate the interparticle bonding of the solid phase. In addition to rapid initial particle rearrangement due to capillary forces, mass transport through liquid is generally orders of magnitude faster than through solid, enhancing the diffusional mechanisms that drive densification. The liquid phase can be obtained either through mixing different powders—melting one component or forming a eutectic—or by sintering at a temperature between the liquidus and solidus. Additionally, since the softer phase is generally the first to melt, the resulting microstructure typically consists of hard particles in a ductile matrix, increasing the toughness of an otherwise brittle component. However, liquid phase sintering is inherently less predictable than solid phase sintering due to the complexity added by the presence of additional phases and rapid solidification rates. Activated sintering is the solid-state analog to the process of liquid phase sintering.














































