In mathematics and physics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace, who first studied its properties. This is often written as

In optics, a Gaussian beam is a beam of electromagnetic radiation with high monochromaticity whose amplitude envelope in the transverse plane is given by a Gaussian function; this also implies a Gaussian intensity (irradiance) profile. This fundamental (or TEM00) transverse Gaussian mode describes the intended output of most (but not all) lasers, as such a beam can be focused into the most concentrated spot. When such a beam is refocused by a lens, the transverse phase dependence is altered; this results in a different Gaussian beam. The electric and magnetic field amplitude profiles along any such circular Gaussian beam (for a given wavelength and polarization) are determined by a single parameter: the so-called waist w0. At any position z relative to the waist (focus) along a beam having a specified w0, the field amplitudes and phases are thereby determined as detailed below.
In radio communication, multipath is the propagation phenomenon that results in radio signals reaching the receiving antenna by two or more paths. Causes of multipath include atmospheric ducting, ionospheric reflection and refraction, and reflection from water bodies and terrestrial objects such as mountains and buildings. When the same signal is received over more than one path, it can create interference and phase shifting of the signal. Destructive interference causes fading; this may cause a radio signal to become too weak in certain areas to be received adequately. For this reason, this effect is also known as multipath interference or multipath distortion.
Phase-shift keying (PSK) is a digital modulation process which conveys data by changing (modulating) the phase of a constant frequency carrier wave. The modulation is accomplished by varying the sine and cosine inputs at a precise time. It is widely used for wireless LANs, RFID and Bluetooth communication.
In fluid mechanics, the Grashof number is a dimensionless number which approximates the ratio of the buoyancy to viscous forces acting on a fluid. It frequently arises in the study of situations involving natural convection and is analogous to the Reynolds number.

In electromagnetism, the Mie solution to Maxwell's equations describes the scattering of an electromagnetic plane wave by a homogeneous sphere. The solution takes the form of an infinite series of spherical multipole partial waves. It is named after German physicist Gustav Mie.
In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the base form
The Friedmann–Lemaître–Robertson–Walker metric is a metric based on the exact solution of the Einstein field equations of general relativity. The metric describes a homogeneous, isotropic, expanding universe that is path-connected, but not necessarily simply connected. The general form of the metric follows from the geometric properties of homogeneity and isotropy; Einstein's field equations are only needed to derive the scale factor of the universe as a function of time. Depending on geographical or historical preferences, the set of the four scientists – Alexander Friedmann, Georges Lemaître, Howard P. Robertson and Arthur Geoffrey Walker – are variously grouped as Friedmann, Friedmann–Robertson–Walker (FRW), Robertson–Walker (RW), or Friedmann–Lemaître (FL). This model is sometimes called the Standard Model of modern cosmology, although such a description is also associated with the further developed Lambda-CDM model. The FLRW model was developed independently by the named authors in the 1920s and 1930s.

In physics, a wave packet is a short burst of localized wave action that travels as a unit, outlined by an envelope. A wave packet can be analyzed into, or can be synthesized from, a potentially-infinite set of component sinusoidal waves of different wavenumbers, with phases and amplitudes such that they interfere constructively only over a small region of space, and destructively elsewhere. Any signal of a limited width in time or space requires many frequency components around a center frequency within a bandwidth inversely proportional to that width; even a gaussian function is considered a wave packet because its Fourier transform is a "packet" of waves of frequencies clustered around a central frequency. Each component wave function, and hence the wave packet, are solutions of a wave equation. Depending on the wave equation, the wave packet's profile may remain constant or it may change (dispersion) while propagating.

A vibration in a string is a wave. Resonance causes a vibrating string to produce a sound with constant frequency, i.e. constant pitch. If the length or tension of the string is correctly adjusted, the sound produced is a musical tone. Vibrating strings are the basis of string instruments such as guitars, cellos, and pianos.
In digital modulation, minimum-shift keying (MSK) is a type of continuous-phase frequency-shift keying that was developed in the late 1950s by Collins Radio employees Melvin L. Doelz and Earl T. Heald. Similar to OQPSK, MSK is encoded with bits alternating between quadrature components, with the Q component delayed by half the symbol period.

In mathematics (specifically multivariable calculus), a multiple integral is a definite integral of a function of several real variables, for instance, f(x, y) or f(x, y, z). Fisical (natur philosofie) interpretation: S any surface, V any volume, etc.. Inkl. variable to time, position, etc.
Pulse compression is a signal processing technique commonly used by radar, sonar and echography to either increase the range resolution when pulse length is constrained or increase the signal to noise ratio when the peak power and the bandwidth of the transmitted signal are constrained. This is achieved by modulating the transmitted pulse and then correlating the received signal with the transmitted pulse.

In optics and especially laser science, the Rayleigh length or Rayleigh range, , is the distance along the propagation direction of a beam from the waist to the place where the area of the cross section is doubled. A related parameter is the confocal parameter, b, which is twice the Rayleigh length. The Rayleigh length is particularly important when beams are modeled as Gaussian beams.
A ratio distribution is a probability distribution constructed as the distribution of the ratio of random variables having two other known distributions. Given two random variables X and Y, the distribution of the random variable Z that is formed as the ratio Z = X/Y is a ratio distribution.
In mathematics, the secondary measure associated with a measure of positive density ρ when there is one, is a measure of positive density μ, turning the secondary polynomials associated with the orthogonal polynomials for ρ into an orthogonal system.
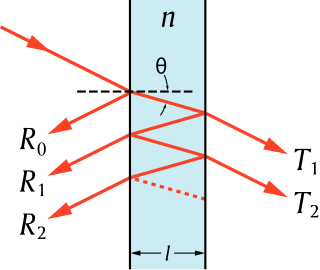
The transfer-matrix method is a method used in optics and acoustics to analyze the propagation of electromagnetic or acoustic waves through a stratified medium; a stack of thin films. This is, for example, relevant for the design of anti-reflective coatings and dielectric mirrors.
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens.
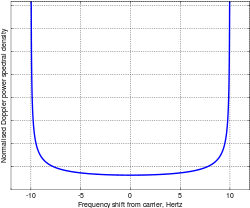
In radio propagation, two-wave with diffuse power (TWDP) fading is a model that explains why a signal strengthens or weakens at certain locations or times. TWDP models fading due to the interference of two strong radio signals and numerous smaller, diffuse signals.
In the field of mathematics known as complex analysis, the indicator function of an entire function indicates the rate of growth of the function in different directions.