
Brownian motion, or pedesis, is the random motion of particles suspended in a medium.
In probability theory, the central limit theorem (CLT) establishes that, in many situations, when independent random variables are summed up, their properly normalized sum tends toward a normal distribution even if the original variables themselves are not normally distributed. The theorem is a key concept in probability theory because it implies that probabilistic and statistical methods that work for normal distributions can be applicable to many problems involving other types of distributions. This theorem has seen many changes during the formal development of probability theory. Previous versions of the theorem date back to 1811, but in its modern general form, this fundamental result in probability theory was precisely stated as late as 1920, thereby serving as a bridge between classical and modern probability theory.

In probability theory and statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional (univariate) normal distribution to higher dimensions. One definition is that a random vector is said to be k-variate normally distributed if every linear combination of its k components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables each of which clusters around a mean value.

In probability theory, a log-normal distribution is a continuous probability distribution of a random variable whose logarithm is normally distributed. Thus, if the random variable X is log-normally distributed, then Y = ln(X) has a normal distribution. Equivalently, if Y has a normal distribution, then the exponential function of Y, X = exp(Y), has a log-normal distribution. A random variable which is log-normally distributed takes only positive real values. It is a convenient and useful model for measurements in exact and engineering sciences, as well as medicine, economics and other topics.
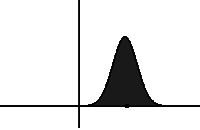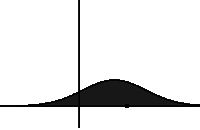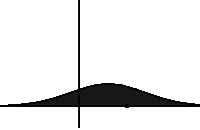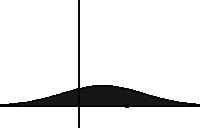
In statistical mechanics, the Fokker–Planck equation is a partial differential equation that describes the time evolution of the probability density function of the velocity of a particle under the influence of drag forces and random forces, as in Brownian motion. The equation can be generalized to other observables as well.

In mathematics, a random walk is a mathematical object, known as a stochastic or random process, that describes a path that consists of a succession of random steps on some mathematical space such as the integers.
In probability theory, a Lévy process, named after the French mathematician Paul Lévy, is a stochastic process with independent, stationary increments: it represents the motion of a point whose successive displacements are random, in which displacements in pairwise disjoint time intervals are independent, and displacements in different time intervals of the same length have identical probability distributions. A Lévy process may thus be viewed as the continuous-time analog of a random walk.

A stochastic differential equation (SDE) is a differential equation in which one or more of the terms is a stochastic process, resulting in a solution which is also a stochastic process. SDEs are used to model various phenomena such as unstable stock prices or physical systems subject to thermal fluctuations. Typically, SDEs contain a variable which represents random white noise calculated as the derivative of Brownian motion or the Wiener process. However, other types of random behaviour are possible, such as jump processes. Random differential equations are conjugate to stochastic differential equations.
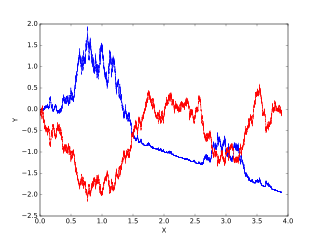
Itô calculus, named after Kiyosi Itô, extends the methods of calculus to stochastic processes such as Brownian motion. It has important applications in mathematical finance and stochastic differential equations.

In mathematics, the Ornstein–Uhlenbeck process is a stochastic process with applications in financial mathematics and the physical sciences. Its original application in physics was as a model for the velocity of a massive Brownian particle under the influence of friction. It is named after Leonard Ornstein and George Eugene Uhlenbeck.
In queueing theory, a discipline within the mathematical theory of probability, a Jackson network is a class of queueing network where the equilibrium distribution is particularly simple to compute as the network has a product-form solution. It was the first significant development in the theory of networks of queues, and generalising and applying the ideas of the theorem to search for similar product-form solutions in other networks has been the subject of much research, including ideas used in the development of the Internet. The networks were first identified by James R. Jackson and his paper was re-printed in the journal Management Science’s ‘Ten Most Influential Titles of Management Sciences First Fifty Years.’
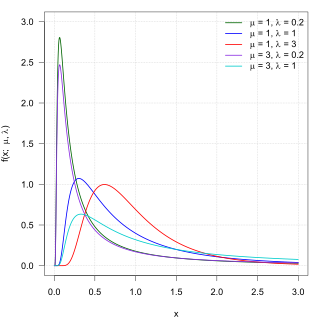
In probability theory, the inverse Gaussian distribution is a two-parameter family of continuous probability distributions with support on (0,∞).
In mathematics, ergodicity expresses the idea that a point of a moving system, either a dynamical system or a stochastic process, will eventually visit all parts of the space that the system moves in, in a uniform and random sense. This implies that the average behavior of the system can be deduced from the trajectory of a "typical" point. Equivalently, a sufficiently large collection of random samples from a process can represent the average statistical properties of the entire process. Ergodicity is a property of the system; it is a statement that the system cannot be reduced or factored into smaller components. Ergodic theory is the study of systems possessing ergodicity.
In mathematics, Gaussian measure is a Borel measure on finite-dimensional Euclidean space Rn, closely related to the normal distribution in statistics. There is also a generalization to infinite-dimensional spaces. Gaussian measures are named after the German mathematician Carl Friedrich Gauss. One reason why Gaussian measures are so ubiquitous in probability theory is the central limit theorem. Loosely speaking, it states that if a random variable X is obtained by summing a large number N of independent random variables of order 1, then X is of order and its law is approximately Gaussian.
The concept of an abstract Wiener space is a mathematical construction developed by Leonard Gross to understand the structure of Gaussian measures on infinite-dimensional spaces. The construction emphasizes the fundamental role played by the Cameron–Martin space. The classical Wiener space is the prototypical example.

In queueing theory, a discipline within the mathematical theory of probability, an M/M/1 queue represents the queue length in a system having a single server, where arrivals are determined by a Poisson process and job service times have an exponential distribution. The model name is written in Kendall's notation. The model is the most elementary of queueing models and an attractive object of study as closed-form expressions can be obtained for many metrics of interest in this model. An extension of this model with more than one server is the M/M/c queue.
In actuarial science and applied probability, ruin theory uses mathematical models to describe an insurer's vulnerability to insolvency/ruin. In such models key quantities of interest are the probability of ruin, distribution of surplus immediately prior to ruin and deficit at time of ruin.
In queueing theory, a discipline within the mathematical theory of probability, a fluid queue is a mathematical model used to describe the fluid level in a reservoir subject to randomly determined periods of filling and emptying. The term dam theory was used in earlier literature for these models. The model has been used to approximate discrete models, model the spread of wildfires, in ruin theory and to model high speed data networks. The model applies the leaky bucket algorithm to a stochastic source.
In queueing theory, a discipline within the mathematical theory of probability, a heavy traffic approximation is the matching of a queueing model with a diffusion process under some limiting conditions on the model's parameters. The first such result was published by John Kingman who showed that when the utilisation parameter of an M/M/1 queue is near 1 a scaled version of the queue length process can be accurately approximated by a reflected Brownian motion.
Exponential Tilting (ET), Exponential Twisting, or Exponential Change of Measure (ECM) is a distribution shifting technique used in many parts of mathematics. The different exponential tiltings of a random variable is known as the natural exponential family of .





















