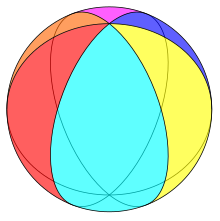
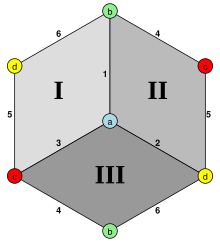
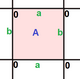
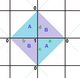
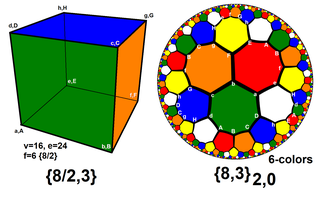
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets, or sides, with three meeting at each vertex. Viewed from a corner, it is a hexagon and its net is usually depicted as a cross.

In geometry, a polyhedron is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices.

In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces, 36 edges, and 24 vertices.

In hyperbolic geometry, the Klein quartic, named after Felix Klein, is a compact Riemann surface of genus 3 with the highest possible order automorphism group for this genus, namely order 168 orientation-preserving automorphisms, and 168 × 2 = 336 automorphisms if orientation may be reversed. As such, the Klein quartic is the Hurwitz surface of lowest possible genus; see Hurwitz's automorphisms theorem. Its (orientation-preserving) automorphism group is isomorphic to PSL(2, 7), the second-smallest non-abelian simple group after the alternating group A5. The quartic was first described in (Klein 1878b).
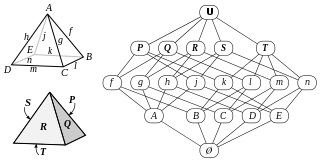
In mathematics, an abstract polytope is an algebraic partially ordered set which captures the dyadic property of a traditional polytope without specifying purely geometric properties such as points and lines.
In the mathematical field of graph theory, the Heawood graph is an undirected graph with 14 vertices and 21 edges, named after Percy John Heawood.
In mathematics, a fundamental polygon can be defined for every compact Riemann surface of genus greater than 0. It encodes not only the topology of the surface through its fundamental group but also determines the Riemann surface up to conformal equivalence. By the uniformization theorem, every compact Riemann surface has simply connected universal covering surface given by exactly one of the following:

In geometry, the hexagonal tiling or hexagonal tessellation is a regular tiling of the Euclidean plane, in which exactly three hexagons meet at each vertex. It has Schläfli symbol of {6,3} or t{3,6} .
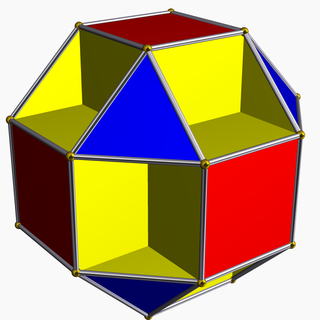
In geometry, the small cubicuboctahedron is a uniform star polyhedron, indexed as U13. It has 20 faces (8 triangles, 6 squares, and 6 octagons), 48 edges, and 24 vertices. Its vertex figure is a crossed quadrilateral.

In geometry and topology, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations.

In topological graph theory, an embedding of a graph on a surface is a representation of on in which points of are associated with vertices and simple arcs are associated with edges in such a way that:

In the mathematical field of graph theory, the Möbius–Kantor graph is a symmetric bipartite cubic graph with 16 vertices and 24 edges named after August Ferdinand Möbius and Seligmann Kantor. It can be defined as the generalized Petersen graph G(8,3): that is, it is formed by the vertices of an octagon, connected to the vertices of an eight-point star in which each point of the star is connected to the points three steps away from it.

In mathematics, a toroid is a surface of revolution with a hole in the middle. The axis of revolution passes through the hole and so does not intersect the surface. For example, when a rectangle is rotated around an axis parallel to one of its edges, then a hollow rectangle-section ring is produced. If the revolved figure is a circle, then the object is called a torus.
In geometry, the regular skew polyhedra are generalizations to the set of regular polyhedra which include the possibility of nonplanar faces or vertex figures. Coxeter looked at skew vertex figures which created new 4-dimensional regular polyhedra, and much later Branko Grünbaum looked at regular skew faces.

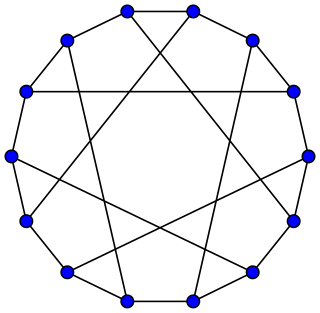
In the mathematical field of graph theory, the Nauru graph is a symmetric, bipartite, cubic graph with 24 vertices and 36 edges. It was named by David Eppstein after the twelve-pointed star in the flag of Nauru.

In geometry, a toroidal polyhedron is a polyhedron which is also a toroid, having a topological genus of 1 or greater. Notable examples include the Császár and Szilassi polyhedra.

In the geometry of 4 dimensions, the 3-3 duoprism or triangular duoprism is a four-dimensional convex polytope. It can be constructed as the Cartesian product of two triangles and is the simplest of an infinite family of four-dimensional polytopes constructed as Cartesian products of two polygons, the duoprisms.

In topological graph theory, the Petrie dual of an embedded graph is another embedded graph that has the Petrie polygons of the first embedding as its faces.