
Osmotic pressure is the minimum pressure which needs to be applied to a solution to prevent the inward flow of its pure solvent across a semipermeable membrane. It is also defined as the measure of the tendency of a solution to take in its pure solvent by osmosis. Potential osmotic pressure is the maximum osmotic pressure that could develop in a solution if it were separated from its pure solvent by a semipermeable membrane

A capillary is a small blood vessel, from 5 to 10 micrometres in diameter, and is part of the microcirculation system. Capillaries are microvessels and the smallest blood vessels in the body. They are composed of only the tunica intima, consisting of a thin wall of simple squamous endothelial cells. They are the site of the exchange of many substances from the surrounding interstitial fluid, and they convey blood from the smallest branches of the arteries (arterioles) to those of the veins (venules). Other substances which cross capillaries include water, oxygen, carbon dioxide, urea, glucose, uric acid, lactic acid and creatinine. Lymph capillaries connect with larger lymph vessels to drain lymphatic fluid collected in microcirculation.

Edema, also spelled oedema, and also known as fluid retention, dropsy, hydropsy and swelling, is the build-up of fluid in the body's tissue. Most commonly, the legs or arms are affected. Symptoms may include skin which feels tight, the area may feel heavy, and joint stiffness. Other symptoms depend on the underlying cause.

Oncotic pressure, or colloid osmotic-pressure, is a type of osmotic pressure induced by the plasma proteins, notably albumin, in a blood vessel's plasma that causes a pull on fluid back into the capillary. Participating colloids displace water molecules, thus creating a relative water molecule deficit with water molecules moving back into the circulatory system within the lower venous pressure end of capillaries.
Hemodynamics or haemodynamics are the dynamics of blood flow. The circulatory system is controlled by homeostatic mechanisms of autoregulation, just as hydraulic circuits are controlled by control systems. The hemodynamic response continuously monitors and adjusts to conditions in the body and its environment. Hemodynamics explains the physical laws that govern the flow of blood in the blood vessels.

The microcirculation is the circulation of the blood in the smallest blood vessels, the microvessels of the microvasculature present within organ tissues. The microvessels include terminal arterioles, metarterioles, capillaries, and venules. Arterioles carry oxygenated blood to the capillaries, and blood flows out of the capillaries through venules into veins.
In chemistry, colligative properties are those properties of solutions that depend on the ratio of the number of solute particles to the number of solvent particles in a solution, and not on the nature of the chemical species present. The number ratio can be related to the various units for concentration of a solution such as molarity, molality, normality (chemistry), etc. The assumption that solution properties are independent of nature of solute particles is exact only for ideal solutions, which are solutions that exhibit thermodynamic properties analogous to those of an ideal gas, and is approximate for dilute real solutions. In other words, colligative properties are a set of solution properties that can be reasonably approximated by the assumption that the solution is ideal.
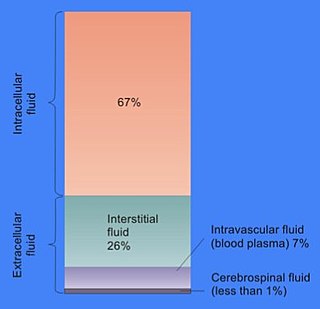
In cell biology, extracellular fluid (ECF) denotes all body fluid outside the cells of any multicellular organism. Total body water in healthy adults is about 50–60% of total body weight; women and the obese typically have a lower percentage than lean men. Extracellular fluid makes up about one-third of body fluid, the remaining two-thirds is intracellular fluid within cells. The main component of the extracellular fluid is the interstitial fluid that surrounds cells.

Renal functions include maintaining an acid–base balance; regulating fluid balance; regulating sodium, potassium, and other electrolytes; clearing toxins; absorption of glucose, amino acids, and other small molecules; regulation of blood pressure; production of various hormones, such as erythropoietin; and activation of vitamin D.

Fluid statics or hydrostatics is the branch of fluid mechanics that studies fluids at hydrostatic equilibrium and "the pressure in a fluid or exerted by a fluid on an immersed body".

The glomerulus is a network of small blood vessels (capillaries) known as a tuft, located at the beginning of a nephron in the kidney. Each of the two kidneys contains about one million nephrons. The tuft is structurally supported by the mesangium, composed of intraglomerular mesangial cells. The blood is filtered across the capillary walls of this tuft through the glomerular filtration barrier, which yields its filtrate of water and soluble substances to a cup-like sac known as Bowman's capsule. The filtrate then enters the renal tubule of the nephron.

The glycocalyx, also known as the pericellular matrix and sometime cell coat, is a glycoprotein and glycolipid covering that surrounds the cell membranes of bacteria, epithelial cells, and other cells. It was described in a review article in 1970.
Water potential is the potential energy of water per unit volume relative to pure water in reference conditions. Water potential quantifies the tendency of water to move from one area to another due to osmosis, gravity, mechanical pressure and matrix effects such as capillary action. The concept of water potential has proved useful in understanding and computing water movement within plants, animals, and soil. Water potential is typically expressed in potential energy per unit volume and very often is represented by the Greek letter ψ.

Osmotic concentration, formerly known as osmolarity, is the measure of solute concentration, defined as the number of osmoles (Osm) of solute per litre (L) of solution. The osmolarity of a solution is usually expressed as Osm/L, in the same way that the molarity of a solution is expressed as "M". Whereas molarity measures the number of moles of solute per unit volume of solution, osmolarity measures the number of osmoles of solute particles per unit volume of solution. This value allows the measurement of the osmotic pressure of a solution and the determination of how the solvent will diffuse across a semipermeable membrane (osmosis) separating two solutions of different osmotic concentration.

In renal physiology, ultrafiltration occurs at the barrier between the blood and the filtrate in the glomerular capsule in the kidneys. As in nonbiological examples of ultrafiltration, pressure and concentration gradients lead to a separation through a semipermeable membrane. The Bowman's capsule contains a dense capillary network called the glomerulus. Blood flows into these capillaries through the afferent arterioles and leaves through the efferent arterioles.
The human body and even its individual body fluids may be conceptually divided into various fluid compartments, which, although not literally anatomic compartments, do represent a real division in terms of how portions of the body's water, solutes, and suspended elements are segregated. The two main fluid compartments are the intracellular and extracellular compartments. The intracellular compartment is the space within the organism's cells; it is separated from the extracellular compartment by cell membranes.
An intercellular cleft is a channel between two cells through which molecules may travel and gap junctions and tight junctions may be present. Most notably, intercellular clefts are often found between epithelial cells and the endothelium of blood vessels and lymphatic vessels, also helping to form the blood-nerve barrier surrounding nerves. Intercellular clefts are important for allowing the transportation of fluids and small solute matter through the endothelium.
Microvasculature comprises the microvessels – venules and capillaries of the microcirculation, with a maximum average diameter of 0.3 millimeters. As the vessels decrease in size, they increase their surface-area-to-volume ratio. This allows surface properties to play a significant role in the function of the vessel.
A depletion force is an effective attractive force that arises between large colloidal particles that are suspended in a dilute solution of depletants, which are smaller solutes that are preferentially excluded from the vicinity of the large particles. One of the earliest reports of depletion forces that lead to particle coagulation is that of Bondy, who observed the separation or "creaming" of rubber latex upon addition of polymer depletant molecules to solution. More generally, depletants can include polymers, micelles, osmolytes, ink, mud, or paint dispersed in a continuous phase.
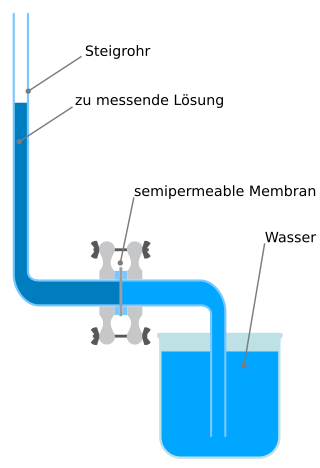
A membrane osmometer is a device used to indirectly measure the number average molecular weight of a polymer sample. One chamber contains pure solvent and the other chamber contains a solution in which the solute is a polymer with an unknown . The osmotic pressure of the solvent across the semipermeable membrane is measured by the membrane osmometer. This osmotic pressure measurement is used to calculate for the sample.


























