In a chemical reaction, chemical equilibrium is the state in which both the reactants and products are present in concentrations which have no further tendency to change with time, so that there is no observable change in the properties of the system. This state results when the forward reaction proceeds at the same rate as the reverse reaction. The reaction rates of the forward and backward reactions are generally not zero, but they are equal. Thus, there are no net changes in the concentrations of the reactants and products. Such a state is known as dynamic equilibrium.
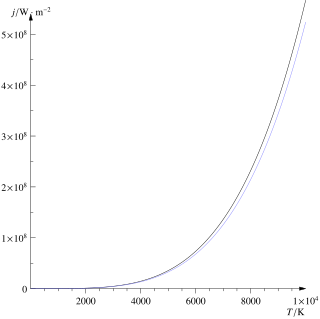
The Stefan–Boltzmann law, also known as Stefan's law, describes the intensity of the thermal radiation emitted by matter in terms of that matter's temperature. It is named for Josef Stefan, who empirically derived the relationship, and Ludwig Boltzmann who derived the law theoretically.

The Boltzmann constant is the proportionality factor that relates the average relative thermal energy of particles in a gas with the thermodynamic temperature of the gas. It occurs in the definitions of the kelvin (K) and the gas constant, and in Planck's law of black-body radiation and Boltzmann's entropy formula, and is used in calculating thermal noise in resistors. The Boltzmann constant has dimensions of energy divided by temperature, the same as entropy. It is named after the Austrian scientist Ludwig Boltzmann.

The kinetic theory of gases is a simple classical model of the thermodynamic behavior of gases. It treats a gas as composed of numerous particles, too small to see with a microscope, which are constantly in random motion. Their collisions with each other and with the walls of their container are used to explain physical properties of the gas—for example, the relationship between its temperature, pressure, and volume. The particles are now known to be the atoms or molecules of the gas.
In physics, a Langevin equation is a stochastic differential equation describing how a system evolves when subjected to a combination of deterministic and fluctuating ("random") forces. The dependent variables in a Langevin equation typically are collective (macroscopic) variables changing only slowly in comparison to the other (microscopic) variables of the system. The fast (microscopic) variables are responsible for the stochastic nature of the Langevin equation. One application is to Brownian motion, which models the fluctuating motion of a small particle in a fluid.

In computational chemistry, molecular physics, and physical chemistry, the Lennard-Jones potential is an intermolecular pair potential. Out of all the intermolecular potentials, the Lennard-Jones potential is probably the one that has been the most extensively studied. It is considered an archetype model for simple yet realistic intermolecular interactions. The Lennard-Jones potential is often used as a building block in molecular models for more complex substances. Many studies of an idealized "Lennard-Jones fluid" use the potential to understand the physical nature of the state of fluids.

Fracture is the appearance of a crack or complete separation of an object or material into two or more pieces under the action of stress. The fracture of a solid usually occurs due to the development of certain displacement discontinuity surfaces within the solid. If a displacement develops perpendicular to the surface, it is called a normal tensile crack or simply a crack; if a displacement develops tangentially, it is called a shear crack, slip band, or dislocation.

In classical statistical mechanics, the equipartition theorem relates the temperature of a system to its average energies. The equipartition theorem is also known as the law of equipartition, equipartition of energy, or simply equipartition. The original idea of equipartition was that, in thermal equilibrium, energy is shared equally among all of its various forms; for example, the average kinetic energy per degree of freedom in translational motion of a molecule should equal that in rotational motion.
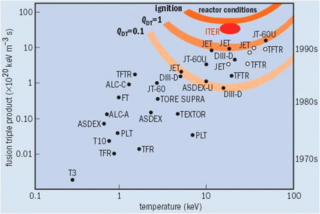
The Lawson criterion is a figure of merit used in nuclear fusion research. It compares the rate of energy being generated by fusion reactions within the fusion fuel to the rate of energy losses to the environment. When the rate of production is higher than the rate of loss, the system will produce net energy. If enough of that energy is captured by the fuel, the system will become self-sustaining and is said to be ignited.
The equilibrium constant of a chemical reaction is the value of its reaction quotient at chemical equilibrium, a state approached by a dynamic chemical system after sufficient time has elapsed at which its composition has no measurable tendency towards further change. For a given set of reaction conditions, the equilibrium constant is independent of the initial analytical concentrations of the reactant and product species in the mixture. Thus, given the initial composition of a system, known equilibrium constant values can be used to determine the composition of the system at equilibrium. However, reaction parameters like temperature, solvent, and ionic strength may all influence the value of the equilibrium constant.

Collision theory is a principle of chemistry used to predict the rates of chemical reactions. It states that when suitable particles of the reactant hit each other with the correct orientation, only a certain amount of collisions result in a perceptible or notable change; these successful changes are called successful collisions. The successful collisions must have enough energy, also known as activation energy, at the moment of impact to break the pre-existing bonds and form all new bonds. This results in the products of the reaction. The activation energy is often predicted using the Transition state theory. Increasing the concentration of the reactant brings about more collisions and hence more successful collisions. Increasing the temperature increases the average kinetic energy of the molecules in a solution, increasing the number of collisions that have enough energy. Collision theory was proposed independently by Max Trautz in 1916 and William Lewis in 1918.
Desorption is the physical process where adsorbed atoms or molecules are released from a surface into the surrounding vacuum or fluid. This occurs when a molecule gains enough energy to overcome the activation barrier and the binding energy that keep it attached to the surface.

Electron paramagnetic resonance (EPR) or electron spin resonance (ESR) spectroscopy is a method for studying materials that have unpaired electrons. The basic concepts of EPR are analogous to those of nuclear magnetic resonance (NMR), but the spins excited are those of the electrons instead of the atomic nuclei. EPR spectroscopy is particularly useful for studying metal complexes and organic radicals. EPR was first observed in Kazan State University by Soviet physicist Yevgeny Zavoisky in 1944, and was developed independently at the same time by Brebis Bleaney at the University of Oxford.
Brunauer–Emmett–Teller (BET) theory aims to explain the physical adsorption of gas molecules on a solid surface and serves as the basis for an important analysis technique for the measurement of the specific surface area of materials. The observations are very often referred to as physical adsorption or physisorption. In 1938, Stephen Brunauer, Paul Hugh Emmett, and Edward Teller presented their theory in the Journal of the American Chemical Society. BET theory applies to systems of multilayer adsorption that usually utilizes a probing gas (called the adsorbate) that does not react chemically with the adsorptive (the material upon which the gas attaches to) to quantify specific surface area. Nitrogen is the most commonly employed gaseous adsorbate for probing surface(s). For this reason, standard BET analysis is most often conducted at the boiling temperature of N2 (77 K). Other probing adsorbates are also utilized, albeit less often, allowing the measurement of surface area at different temperatures and measurement scales. These include argon, carbon dioxide, and water. Specific surface area is a scale-dependent property, with no single true value of specific surface area definable, and thus quantities of specific surface area determined through BET theory may depend on the adsorbate molecule utilized and its adsorption cross section.

In chemistry, transition state theory (TST) explains the reaction rates of elementary chemical reactions. The theory assumes a special type of chemical equilibrium (quasi-equilibrium) between reactants and activated transition state complexes.
Diffusivity, mass diffusivity or diffusion coefficient is usually written as the proportionality constant between the molar flux due to molecular diffusion and the negative value of the gradient in the concentration of the species. More accurately, the diffusion coefficient times the local concentration is the proportionality constant between the negative value of the mole fraction gradient and the molar flux. This distinction is especially significant in gaseous systems with strong temperature gradients. Diffusivity derives its definition from Fick's law and plays a role in numerous other equations of physical chemistry.
In radiometry, radiosity is the radiant flux leaving a surface per unit area, and spectral radiosity is the radiosity of a surface per unit frequency or wavelength, depending on whether the spectrum is taken as a function of frequency or of wavelength. The SI unit of radiosity is the watt per square metre, while that of spectral radiosity in frequency is the watt per square metre per hertz (W·m−2·Hz−1) and that of spectral radiosity in wavelength is the watt per square metre per metre (W·m−3)—commonly the watt per square metre per nanometre. The CGS unit erg per square centimeter per second is often used in astronomy. Radiosity is often called intensity in branches of physics other than radiometry, but in radiometry this usage leads to confusion with radiant intensity.

Viscoplasticity is a theory in continuum mechanics that describes the rate-dependent inelastic behavior of solids. Rate-dependence in this context means that the deformation of the material depends on the rate at which loads are applied. The inelastic behavior that is the subject of viscoplasticity is plastic deformation which means that the material undergoes unrecoverable deformations when a load level is reached. Rate-dependent plasticity is important for transient plasticity calculations. The main difference between rate-independent plastic and viscoplastic material models is that the latter exhibit not only permanent deformations after the application of loads but continue to undergo a creep flow as a function of time under the influence of the applied load.
Chapman–Enskog theory provides a framework in which equations of hydrodynamics for a gas can be derived from the Boltzmann equation. The technique justifies the otherwise phenomenological constitutive relations appearing in hydrodynamical descriptions such as the Navier–Stokes equations. In doing so, expressions for various transport coefficients such as thermal conductivity and viscosity are obtained in terms of molecular parameters. Thus, Chapman–Enskog theory constitutes an important step in the passage from a microscopic, particle-based description to a continuum hydrodynamical one.
Heat transfer physics describes the kinetics of energy storage, transport, and energy transformation by principal energy carriers: phonons, electrons, fluid particles, and photons. Heat is thermal energy stored in temperature-dependent motion of particles including electrons, atomic nuclei, individual atoms, and molecules. Heat is transferred to and from matter by the principal energy carriers. The state of energy stored within matter, or transported by the carriers, is described by a combination of classical and quantum statistical mechanics. The energy is different made (converted) among various carriers. The heat transfer processes are governed by the rates at which various related physical phenomena occur, such as the rate of particle collisions in classical mechanics. These various states and kinetics determine the heat transfer, i.e., the net rate of energy storage or transport. Governing these process from the atomic level to macroscale are the laws of thermodynamics, including conservation of energy.















































