
Shading refers to the depiction of depth perception in 3D models or illustrations by varying the level of darkness. Shading tries to approximate local behavior of light on the object's surface and is not to be confused with techniques of adding shadows, such as shadow mapping or shadow volumes, which fall under global behavior of light.

In 3D computer graphics, hidden-surface determination is the process of identifying what surfaces and parts of surfaces can be seen from a particular viewing angle. A hidden-surface determination algorithm is a solution to the visibility problem, which was one of the first major problems in the field of 3D computer graphics. The process of hidden-surface determination is sometimes called hiding, and such an algorithm is sometimes called a hider. When referring to line rendering it is known as hidden-line removal. Hidden-surface determination is necessary to render a scene correctly, so that one may not view features hidden behind the model itself, allowing only the naturally viewable portion of the graphic to be visible.

In 3D computer graphics and solid modeling, a polygon mesh is a collection of vertices, edges and faces that defines the shape of a polyhedral object. The faces usually consist of triangles, quadrilaterals (quads), or other simple convex polygons (n-gons), since this simplifies rendering, but may also be more generally composed of concave polygons, or even polygons with holes.

In computer graphics, a shader is a computer program that calculates the appropriate levels of light, darkness, and color during the rendering of a 3D scene—a process known as shading. Shaders have evolved to perform a variety of specialized functions in computer graphics special effects and video post-processing, as well as general-purpose computing on graphics processing units.
OBJ is a geometry definition file format first developed by Wavefront Technologies for its Advanced Visualizer animation package. The file format is open and has been adopted by other 3D graphics application vendors.

In computer graphics, back-face culling determines whether a polygon of a graphical object is drawn. It is a step in the graphical pipeline that tests whether the points in the polygon appear in clockwise or counter-clockwise order when projected onto the screen. If the user has specified that front-facing polygons have a clockwise winding, but the polygon projected on the screen has a counter-clockwise winding then it has been rotated to face away from the camera and will not be drawn.

In 3D computer graphics, polygonal modeling is an approach for modeling objects by representing or approximating their surfaces using polygon meshes. Polygonal modeling is well suited to scanline rendering and is therefore the method of choice for real-time computer graphics. Alternate methods of representing 3D objects include NURBS surfaces, subdivision surfaces, and equation-based representations used in ray tracers.
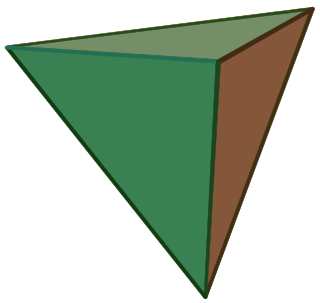
In geometry, a uniform polyhedron has regular polygons as faces and is vertex-transitive. It follows that all vertices are congruent.
A quad-edge data structure is a computer representation of the topology of a two-dimensional or three-dimensional map, that is, a graph drawn on a (closed) surface. It was first described by Jorge Stolfi and Leonidas J. Guibas. It is a variant of the earlier winged edge data structure.

In computer graphics, a triangle mesh is a type of polygon mesh. It comprises a set of triangles that are connected by their common edges or vertices.
PLY is a computer file format known as the Polygon File Format or the Stanford Triangle Format. It was principally designed to store three-dimensional data from 3D scanners. The data storage format supports a relatively simple description of a single object as a list of nominally flat polygons. A variety of properties can be stored, including color and transparency, surface normals, texture coordinates and data confidence values. The format permits one to have different properties for the front and back of a polygon.
Java Binding for the OpenGL API is a JSR API specification for the Java Platform, Standard Edition which allows to use OpenGL on the Java. There is also Java Binding for the OpenGL ES API for the Java Platform, Micro Edition.
In geometry, a uniform tiling is a tessellation of the plane by regular polygon faces with the restriction of being vertex-transitive.
A vertex buffer object (VBO) is an OpenGL feature that provides methods for uploading vertex data to the video device for non-immediate-mode rendering. VBOs offer substantial performance gains over immediate mode rendering primarily because the data reside in video device memory rather than system memory and so it can be rendered directly by the video device. These are equivalent to vertex buffers in Direct3D.
Additive manufacturing file format (AMF) is an open standard for describing objects for additive manufacturing processes such as 3D printing. The official ISO/ASTM 52915:2016 standard is an XML-based format designed to allow any computer-aided design software to describe the shape and composition of any 3D object to be fabricated on any 3D printer via a computer-aided manufacturing software. Unlike its predecessor STL format, AMF has native support for color, materials, lattices, and constellations.
In geometry of 4 dimensions or higher, a double pyramid, duopyramid, or fusil is a polytope constructed by 2 orthogonal polytopes with edges connecting all pairs of vertices between the two. The term fusil is used by Norman Johnson as a rhombic-shape. The term duopyramid was used by George Olshevsky, as the dual of a duoprism.
In graph drawing and geometric graph theory, a Tutte embedding or barycentric embedding of a simple, 3-vertex-connected, planar graph is a crossing-free straight-line embedding with the properties that the outer face is a convex polygon and that each interior vertex is at the average of its neighbors' positions. If the outer polygon is fixed, this condition on the interior vertices determines their position uniquely as the solution to a system of linear equations. Solving the equations geometrically produces a planar embedding. Tutte's spring theorem, proven by W. T. Tutte (1963), states that this unique solution is always crossing-free, and more strongly that every face of the resulting planar embedding is convex. It is called the spring theorem because such an embedding can be found as the equilibrium position for a system of springs representing the edges of the graph.
3D Manufacturing Format or 3MF is an open source file format standard developed and published by the 3MF Consortium.
This is a glossary of terms relating to computer graphics.
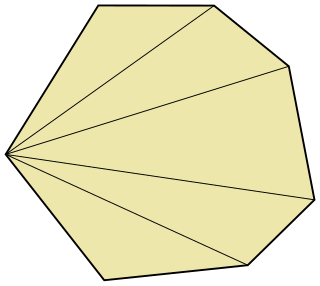
In computational geometry, a fan triangulation is a simple way to triangulate a polygon by choosing a vertex and drawing edges to all of the other vertices of the polygon. Not every polygon can be triangulated this way, so this method is usually only used for convex polygons.










