In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the polynomial (x + y)n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with b + c = n, and the coefficient a of each term is a specific positive integer depending on n and b. For example, for n = 4,

The number e is a mathematical constant approximately equal to 2.71828 that can be characterized in many ways. It is the base of the natural logarithm function. It is the limit of as n tends to infinity, an expression that arises in the computation of compound interest. It is the value at 1 of the (natural) exponential function, commonly denoted It is also the sum of the infinite series

The exponential function is a mathematical function denoted by or . Unless otherwise specified, the term generally refers to the positive-valued function of a real variable, although it can be extended to the complex numbers or generalized to other mathematical objects like matrices or Lie algebras. The exponential function originated from the operation of taking powers of a number, but various modern definitions allow it to be rigorously extended to all real arguments , including irrational numbers. Its ubiquitous occurrence in pure and applied mathematics led mathematician Walter Rudin to consider the exponential function to be "the most important function in mathematics".
In mathematics, the factorial of a non-negative integer , denoted by , is the product of all positive integers less than or equal to . The factorial of also equals the product of with the next smaller factorial:
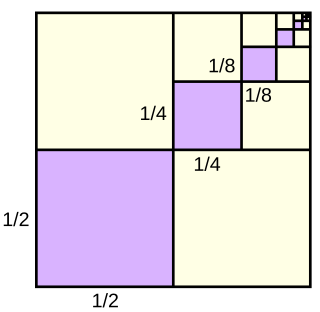
In mathematics, a geometric series is the sum of an infinite number of terms that have a constant ratio between successive terms. For example, the series

In mathematics, the geometric mean is a mean or average which indicates a central tendency of a finite set of real numbers by using the product of their values. The geometric mean is defined as the nth root of the product of n numbers, i.e., for a set of numbers a1, a2, ..., an, the geometric mean is defined as

In mathematics, the logarithm is the inverse function to exponentiation. That means that the logarithm of a number x to the base b is the exponent to which b must be raised to produce x. For example, since 1000 = 103, the logarithm base of 1000 is 3, or log10 (1000) = 3. The logarithm of x to base b is denoted as logb (x), or without parentheses, logb x. When the base is clear from the context or is irrelevant, such as in big O notation, it is sometimes written log x.

In probability theory and statistics, the geometric distribution is either one of two discrete probability distributions:

In mathematics, exponentiation is an operation involving two numbers: the base and the exponent or power. Exponentiation is written as bn, where b is the base and n is the power; this is pronounced as "b (raised) to the n". When n is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, bn is the product of multiplying n bases:

Exponential growth is a process that increases quantity over time at an ever-increasing rate. It occurs when the instantaneous rate of change of a quantity with respect to time is proportional to the quantity itself. Described as a function, a quantity undergoing exponential growth is an exponential function of time, that is, the variable representing time is the exponent. Exponential growth is the inverse of logarithmic growth.

The square root of 2 is a positive real number that, when multiplied by itself or squared, equals the number 2. It may be written in mathematics as or . It is an algebraic number, and therefore not a transcendental number. Technically, it should be called the principal square root of 2, to distinguish it from the negative number with the same property.

A power of two is a number of the form 2n where n is an integer, that is, the result of exponentiation with number two as the base and integer n as the exponent.

In mathematics, tetration is an operation based on iterated, or repeated, exponentiation. There is no standard notation for tetration, though Knuth's up arrow notation and the left-exponent xb are common.
In the mathematical subject of geometric group theory, the growth rate of a group with respect to a symmetric generating set describes how fast a group grows. Every element in the group can be written as a product of generators, and the growth rate counts the number of elements that can be written as a product of length n.
The doubling time is the time it takes for a population to double in size/value. It is applied to population growth, inflation, resource extraction, consumption of goods, compound interest, the volume of malignant tumours, and many other things that tend to grow over time. When the relative growth rate is constant, the quantity undergoes exponential growth and has a constant doubling time or period, which can be calculated directly from the growth rate.
In mathematics, a combinatorial explosion is the rapid growth of the complexity of a problem due to how the combinatorics of the problem is affected by the input, constraints, and bounds of the problem. Combinatorial explosion is sometimes used to justify the intractability of certain problems. Examples of such problems include certain mathematical functions, the analysis of some puzzles and games, and some pathological examples which can be modelled as the Ackermann function.

A double exponential function is a constant raised to the power of an exponential function. The general formula is (where a>1 and b>1), which grows much more quickly than an exponential function. For example, if a = b = 10:
In combinatorial mathematics, a rook polynomial is a generating polynomial of the number of ways to place non-attacking rooks on a board that looks like a checkerboard; that is, no two rooks may be in the same row or column. The board is any subset of the squares of a rectangular board with m rows and n columns; we think of it as the squares in which one is allowed to put a rook. The board is the ordinary chessboard if all squares are allowed and m = n = 8 and a chessboard of any size if all squares are allowed and m = n. The coefficient of x k in the rook polynomial RB(x) is the number of ways k rooks, none of which attacks another, can be arranged in the squares of B. The rooks are arranged in such a way that there is no pair of rooks in the same row or column. In this sense, an arrangement is the positioning of rooks on a static, immovable board; the arrangement will not be different if the board is rotated or reflected while keeping the squares stationary. The polynomial also remains the same if rows are interchanged or columns are interchanged.

A geometric progression, also known as a geometric sequence, is a mathematical sequence of non-zero numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression with common ratio 3. Similarly 10, 5, 2.5, 1.25, ... is a geometric sequence with common ratio 1/2.
A mathematical constant is a key number whose value is fixed by an unambiguous definition, often referred to by a special symbol, or by mathematicians' names to facilitate using it across multiple mathematical problems. Constants arise in many areas of mathematics, with constants such as e and π occurring in such diverse contexts as geometry, number theory, statistics, and calculus.































