Abel's binomial theorem, named after Niels Henrik Abel, is a mathematical identity involving sums of binomial coefficients. It states the following:
Abel's binomial theorem, named after Niels Henrik Abel, is a mathematical identity involving sums of binomial coefficients. It states the following:

In probability theory and statistics, the binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a sequence of n independent experiments, each asking a yes–no question, and each with its own Boolean-valued outcome: success or failure. A single success/failure experiment is also called a Bernoulli trial or Bernoulli experiment, and a sequence of outcomes is called a Bernoulli process; for a single trial, i.e., n = 1, the binomial distribution is a Bernoulli distribution. The binomial distribution is the basis for the popular binomial test of statistical significance.

In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers n ≥ k ≥ 0 and is written It is the coefficient of the xk term in the polynomial expansion of the binomial power (1 + x)n, and is given by the formula
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the polynomial (x + y)n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with b + c = n, and the coefficient a of each term is a specific positive integer depending on n and b. For example, for n = 4,
In mathematics, the Bernoulli numbersBn are a sequence of rational numbers which occur frequently in analysis. The Bernoulli numbers appear in the Taylor series expansions of the tangent and hyperbolic tangent functions, in Faulhaber's formula for the sum of m-th powers of the first n positive integers, in the Euler–Maclaurin formula, and in expressions for certain values of the Riemann zeta function.

In probability theory and statistics, the negative binomial distribution is a discrete probability distribution that models the number of successes in a sequence of independent and identically distributed Bernoulli trials before a specified (non-random) number of failures occur. For example, we can define rolling a 6 on a die as a failure, and rolling any other number as a success, and ask how many successful rolls will occur before we see the third failure. In such a case, the probability distribution of the number of non-6s that appear will be a negative binomial distribution. We could similarly use the negative binomial distribution to model the number of days a certain machine works before it breaks down. It is a kind of binomial distribution.
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients that arises in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Blaise Pascal, although other mathematicians studied it centuries before him in India, Persia, China, Germany, and Italy.
In mathematical analysis, the Lagrange inversion theorem, also known as the Lagrange–Bürmann formula, gives the Taylor series expansion of the inverse function of an analytic function.
In mathematics, a generating function is a way of encoding an infinite sequence of numbers (an) by treating them as the coefficients of a formal power series. This series is called the generating function of the sequence. Unlike an ordinary series, the formal power series is not required to converge: in fact, the generating function is not actually regarded as a function, and the "variable" remains an indeterminate. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general linear recurrence problem. One can generalize to formal power series in more than one indeterminate, to encode information about infinite multi-dimensional arrays of numbers.
In mathematics, the falling factorial is defined as the polynomial
In mathematics, Abel's theorem for power series relates a limit of a power series to the sum of its coefficients. It is named after Norwegian mathematician Niels Henrik Abel.
In mathematics, the binomial series is the Taylor series for the function given by where is an arbitrary complex number and |x| < 1. Explicitly,
In mathematical analysis, Cesàro summation assigns values to some infinite sums that are not necessarily convergent in the usual sense. The Cesàro sum is defined as the limit, as n tends to infinity, of the sequence of arithmetic means of the first n partial sums of the series.
In combinatorics, Vandermonde's identity is the following identity for binomial coefficients:
In combinatorics, the binomial transform is a sequence transformation that computes its forward differences. It is closely related to the Euler transform, which is the result of applying the binomial transform to the sequence associated with its ordinary generating function.
In mathematics, Faulhaber's formula, named after the early 17th century mathematician Johann Faulhaber, expresses the sum of the p-th powers of the first n positive integers
In the mathematics of convergent and divergent series, Euler summation is a summability method. That is, it is a method for assigning a value to a series, different from the conventional method of taking limits of partial sums. Given a series Σan, if its Euler transform converges to a sum, then that sum is called the Euler sum of the original series. As well as being used to define values for divergent series, Euler summation can be used to speed the convergence of series.
In mathematics, in the area of combinatorics, a q-Pochhammer symbol, also called a q-shifted factorial, is a q-analog of the Pochhammer symbol. It is defined as
In mathematics, the Schuette–Nesbitt formula is a generalization of the inclusion–exclusion principle. It is named after Donald R. Schuette and Cecil J. Nesbitt.
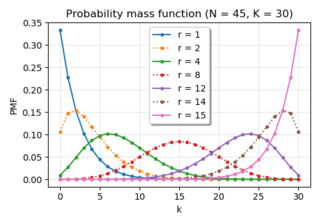
In probability theory and statistics, the negative hypergeometric distribution describes probabilities for when sampling from a finite population without replacement in which each sample can be classified into two mutually exclusive categories like Pass/Fail, Male/Female or Employed/Unemployed. As random selections are made from the population, each subsequent draw decreases the population causing the probability of success to change with each draw. Unlike the standard hypergeometric distribution, which describes the number of successes in a fixed sample size, in the negative hypergeometric distribution, samples are drawn until failures have been found, and the distribution describes the probability of finding successes in such a sample. In other words, the negative hypergeometric distribution describes the likelihood of successes in a sample with exactly failures.
In mathematics, a transformation of a sequence's generating function provides a method of converting the generating function for one sequence into a generating function enumerating another. These transformations typically involve integral formulas applied to a sequence generating function or weighted sums over the higher-order derivatives of these functions.