In computer science, an abstract data type (ADT) is a mathematical model for data types, defined by its behavior (semantics) from the point of view of a user of the data, specifically in terms of possible values, possible operations on data of this type, and the behavior of these operations. This mathematical model contrasts with data structures, which are concrete representations of data, and are the point of view of an implementer, not a user. For example, a stack has push/pop operations that follow a Last-In-First-Out rule, and can be concretely implemented using either a list or an array. Another example is a set which stores values, without any particular order, and no repeated values. Values themselves are not retrieved from sets; rather, one tests a value for membership to obtain a Boolean "in" or "not in".
Abstraction is a process where general rules and concepts are derived from the use and classifying of specific examples, literal signifiers, first principles, or other methods.

A concept is an abstract idea that serves as a foundation for more concrete principles, thoughts, and beliefs. Concepts play an important role in all aspects of cognition. As such, concepts are studied within such disciplines as linguistics, psychology, and philosophy, and these disciplines are interested in the logical and psychological structure of concepts, and how they are put together to form thoughts and sentences. The study of concepts has served as an important flagship of an emerging interdisciplinary approach, cognitive science.
Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory, algebra, geometry, analysis, and set theory.
Philosophy of mathematics is the branch of philosophy that deals with the nature of mathematics and its relationship to other areas of philosophy, particularly epistemology and metaphysics. Central questions posed include whether or not mathematical objects are purely abstract entities or are in some way concrete, and in what the relationship such objects have with physical reality consists.
In computer science, denotational semantics is an approach of formalizing the meanings of programming languages by constructing mathematical objects that describe the meanings of expressions from the languages. Other approaches providing formal semantics of programming languages include axiomatic semantics and operational semantics.
In software engineering and computer science, abstraction is the process of generalizing concrete details, such as attributes, away from the study of objects and systems to focus attention on details of greater importance. Abstraction is a fundamental concept in computer science and software engineering, especially within the object-oriented programming paradigm. Examples of this include:
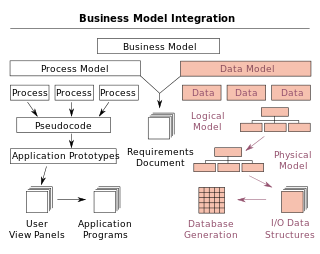
A data model is an abstract model that organizes elements of data and standardizes how they relate to one another and to the properties of real-world entities. For instance, a data model may specify that the data element representing a car be composed of a number of other elements which, in turn, represent the color and size of the car and define its owner.
Foundations of mathematics are the logical and mathematical framework that allows the development of mathematics without generating self-contradictory theories, and, in particular, to have reliable concepts of theorems, proofs, algorithms, etc. This may also include the philosophical study of the relation of this framework with reality.
A modeling language is any artificial language that can be used to express data, information or knowledge or systems in a structure that is defined by a consistent set of rules. The rules are used for interpretation of the meaning of components in the structure of a programming language.
A formal system is an abstract structure and formalization of an axiomatic system used for deducing, using rules of inference, theorems from axioms by a set of inference rules.

In natural language and physical science, a physical object or material object is a contiguous collection of matter, within a defined boundary, that exists in space and time. Usually contrasted with abstract objects and mental objects.
The term conceptual model refers to any model that is formed after a conceptualization or generalization process. Conceptual models are often abstractions of things in the real world, whether physical or social. Semantic studies are relevant to various stages of concept formation. Semantics is fundamentally a study of concepts, the meaning that thinking beings give to various elements of their experience.
Formal science is a branch of science studying disciplines concerned with abstract structures described by formal systems, such as logic, mathematics, statistics, theoretical computer science, artificial intelligence, information theory, game theory, systems theory, decision theory and theoretical linguistics. Whereas the natural sciences and social sciences seek to characterize physical systems and social systems, respectively, using empirical methods, the formal sciences use language tools concerned with characterizing abstract structures described by formal systems. The formal sciences aid the natural and social sciences by providing information about the structures used to describe the physical world, and what inferences may be made about them.
Concept learning, also known as category learning, concept attainment, and concept formation, is defined by Bruner, Goodnow, & Austin (1956) as "the search for and testing of attributes that can be used to distinguish exemplars from non exemplars of various categories". More simply put, concepts are the mental categories that help us classify objects, events, or ideas, building on the understanding that each object, event, or idea has a set of common relevant features. Thus, concept learning is a strategy which requires a learner to compare and contrast groups or categories that contain concept-relevant features with groups or categories that do not contain concept-relevant features.
Reification is a fallacy of ambiguity, when an abstraction is treated as if it were a concrete real event or physical entity. In other words, it is the error of treating something that is not concrete, such as an idea, as a concrete thing. A common case of reification is the confusion of a model with reality: "the map is not the territory".

A mathematical object is an abstract concept arising in mathematics. Typically, a mathematical object can be a value that can be assigned to a symbol, and therefore can be involved in formulas. Commonly encountered mathematical objects include numbers, expressions, shapes, functions, and sets. Mathematical objects can be very complex; for example, theorems, proofs, and even formal theories are considered as mathematical objects in proof theory.
Philosophy of logic is the area of philosophy that studies the scope and nature of logic. It investigates the philosophical problems raised by logic, such as the presuppositions often implicitly at work in theories of logic and in their application. This involves questions about how logic is to be defined and how different logical systems are connected to each other. It includes the study of the nature of the fundamental concepts used by logic and the relation of logic to other disciplines. According to a common characterisation, philosophical logic is the part of the philosophy of logic that studies the application of logical methods to philosophical problems, often in the form of extended logical systems like modal logic. But other theorists draw the distinction between the philosophy of logic and philosophical logic differently or not at all. Metalogic is closely related to the philosophy of logic as the discipline investigating the properties of formal logical systems, like consistency and completeness.

Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics.
This glossary of computer science is a list of definitions of terms and concepts used in computer science, its sub-disciplines, and related fields, including terms relevant to software, data science, and computer programming.