Active fluid

Last updated

An active fluid is a densely packed soft material whose constituent elements can self-propel. [1] [2] [3] [4] Examples include dense suspensions of bacteria, microtubule networks or artificial swimmers. [2] These materials come under the broad category of active matter and differ significantly in properties when compared to passive fluids, [5] which can be described using Navier-Stokes equation. Even though systems describable as active fluids have been observed and investigated in different contexts for a long time, scientific interest in properties directly related to the activity has emerged only in the past two decades. These materials have been shown to exhibit a variety of different phases ranging from well ordered patterns to chaotic states (see below). Recent experimental investigations have suggested that the various dynamical phases exhibited by active fluids may have important technological applications. [6] [7]

Contents

Terminology

The terms “active fluids”, “active nematics” and “active liquid crystals” have been used almost synonymously to denote hydrodynamic descriptions of dense active matter. [2] [8] [9] [10] While in many respects they describe the same phenomenon, there are subtle differences between them. “Active nematics” and “active liquid crystals” refers to systems where the constituent elements have nematic order whereas “active fluids” is the more generic term combining systems with both nematic and polar interactions.

Examples and observations

There are wide range of cellular and intracellular elements which form active fluids. This include systems of microtubule, bacteria, sperm cells as well as inanimate microswimmers. [2] It is known that these systems form a variety of structures such as regular and irregular lattices as well as seemingly random states in two dimensions.

Pattern formation

Active fluids have been shown to organize into regular and irregular lattices in a variety of settings. These include irregular hexagonal lattices by microtubules [11] and regular vortex lattice by sperm cells. [12] From topological considerations, it can be seen that the constituent element in quasi stationary states of active fluids should necessarily be vortices. But very less is known, for instance, about the length scale selection in such systems.

Active turbulence

Chaotic states exhibited by active fluids are termed as active turbulence. [13] Such states are qualitatively similar to hydrodynamic turbulence, by virtue of which they are termed active turbulence. But recent research has indicated that the statistical properties associated with such flows are quite different from that of hydrodynamic turbulence. [5] [14]

Mechanism and modelling approaches

The mechanism behind the formation of various structures in active fluids is an area of active research. It is well understood that the structure formation in active fluids is intimately related to defects or disclinations in the order parameter field [15] [16] (the orientational order of the constituent agents). An important part of research on active fluids involve modelling of dynamics of these defects to study its role in pattern formation and turbulent dynamics in active fluids. Modified versions of Vicsek model are among earliest and continually used approach to model active fluids. [17] Such models have been shown to capture the various dynamical states exhibited by active fluids. [17] More refined approaches include derivation of continuum limit hydrodynamic equations for active fluids [18] [19] and adaptation of liquid crystal theory by including the activity terms. [13]

Potential applications

A few technological applications for active fluids have been proposed such as powering of molecular motors through active turbulence and patterned state. [7] Furthermore, given the innumerable applications liquid crystals find in various technologies, there have been proposals to augment them by using active liquid crystals. [20]

See also

Related Research Articles

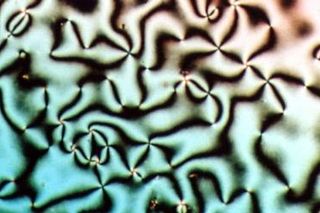
<span class="mw-page-title-main">Liquid crystal</span> State of matter with properties of both conventional liquids and crystals

Liquid crystal (LC) is a state of matter whose properties are between those of conventional liquids and those of solid crystals. For example, a liquid crystal can flow like a liquid, but its molecules may be oriented in a common direction as in solid. There are many types of LC phases, which can be distinguished by their optical properties. The contrasting textures arise due to molecules within one area of material ("domain") being oriented in the same direction but different areas having different orientations. An LC material may not always be in an LC state of matter.

Superfluid helium-4 is the superfluid form of helium-4, an isotope of the element helium. A superfluid is a state of matter in which matter behaves like a fluid with zero viscosity. The substance, which looks like a normal liquid, flows without friction past any surface, which allows it to continue to circulate over obstructions and through pores in containers which hold it, subject only to its own inertia.

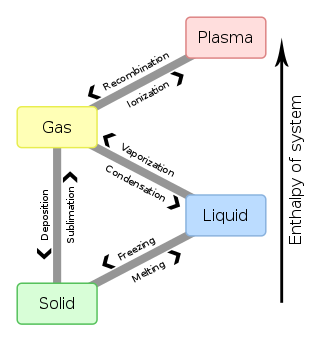
<span class="mw-page-title-main">Phase transition</span> Physical process of transition between basic states of matter

In chemistry, thermodynamics, and other related fields, a phase transition is the physical process of transition between one state of a medium and another. Commonly the term is used to refer to changes among the basic states of matter: solid, liquid, and gas, and in rare cases, plasma. A phase of a thermodynamic system and the states of matter have uniform physical properties. During a phase transition of a given medium, certain properties of the medium change as a result of the change of external conditions, such as temperature or pressure. This can be a discontinuous change; for example, a liquid may become gas upon heating to its boiling point, resulting in an abrupt change in volume. The identification of the external conditions at which a transformation occurs defines the phase transition point.

Quantum turbulence is the name given to the turbulent flow – the chaotic motion of a fluid at high flow rates – of quantum fluids, such as superfluids. The idea that a form of turbulence might be possible in a superfluid via the quantized vortex lines was first suggested by Richard Feynman. The dynamics of quantum fluids are governed by quantum mechanics, rather than classical physics which govern classical (ordinary) fluids. Some examples of quantum fluids include superfluid helium, Bose–Einstein condensates (BECs), polariton condensates, and nuclear pasta theorized to exist inside neutron stars. Quantum fluids exist at temperatures below the critical temperature at which Bose-Einstein condensation takes place.

The λ (lambda) universality class is a group in condensed matter physics. It regroups several systems possessing strong analogies, namely, superfluids, superconductors and smectics. All these systems are expected to belong to the same universality class for the thermodynamic critical properties of the phase transition. While these systems are quite different at the first glance, they all are described by similar formalisms and their typical phase diagrams are identical.

<span class="mw-page-title-main">Quantum vortex</span> Quantized flux circulation of some physical quantity

In physics, a quantum vortex represents a quantized flux circulation of some physical quantity. In most cases, quantum vortices are a type of topological defect exhibited in superfluids and superconductors. The existence of quantum vortices was first predicted by Lars Onsager in 1949 in connection with superfluid helium. Onsager reasoned that quantisation of vorticity is a direct consequence of the existence of a superfluid order parameter as a spatially continuous wavefunction. Onsager also pointed out that quantum vortices describe the circulation of superfluid and conjectured that their excitations are responsible for superfluid phase transitions. These ideas of Onsager were further developed by Richard Feynman in 1955 and in 1957 were applied to describe the magnetic phase diagram of type-II superconductors by Alexei Alexeyevich Abrikosov. In 1935 Fritz London published a very closely related work on magnetic flux quantization in superconductors. London's fluxoid can also be viewed as a quantum vortex.

<span class="mw-page-title-main">Subir Sachdev</span> Indian physicist

Subir Sachdev is Herchel Smith Professor of Physics at Harvard University specializing in condensed matter. He was elected to the U.S. National Academy of Sciences in 2014, and received the Lars Onsager Prize from the American Physical Society and the Dirac Medal from the ICTP in 2018. He was a co-editor of the Annual Review of Condensed Matter Physics from 2017–2019.

Multi-particle collision dynamics (MPC), also known as stochastic rotation dynamics (SRD), is a particle-based mesoscale simulation technique for complex fluids which fully incorporates thermal fluctuations and hydrodynamic interactions. Coupling of embedded particles to the coarse-grained solvent is achieved through molecular dynamics.

<span class="mw-page-title-main">Active matter</span> Matter behavior at system scale

Active matter is matter composed of large numbers of active "agents", each of which consumes energy in order to move or to exert mechanical forces. Such systems are intrinsically out of thermal equilibrium. Unlike thermal systems relaxing towards equilibrium and systems with boundary conditions imposing steady currents, active matter systems break time reversal symmetry because energy is being continually dissipated by the individual constituents. Most examples of active matter are biological in origin and span all the scales of the living, from bacteria and self-organising bio-polymers such as microtubules and actin, to schools of fish and flocks of birds. However, a great deal of current experimental work is devoted to synthetic systems such as artificial self-propelled particles. Active matter is a relatively new material classification in soft matter: the most extensively studied model, the Vicsek model, dates from 1995.

<span class="mw-page-title-main">Michael Cates</span> British physicist

Michael Elmhirst Cates is a British physicist. He is the 19th Lucasian Professor of Mathematics at the University of Cambridge and has held this position since 1 July 2015. He was previously Professor of Natural Philosophy at the University of Edinburgh, and has held a Royal Society Research Professorship since 2007.

<span class="mw-page-title-main">Julia Yeomans</span> British theoretical physicist (born 1954)

Julia Mary Yeomans is a British theoretical physicist active in the fields of soft condensed matter and biological physics. She has served as Professor of Physics at the University of Oxford since 2002.

<span class="mw-page-title-main">John F. Brady (chemical engineer)</span> American chemical engineer and professor

John Francis Brady is an American chemical engineer and the Chevron Professor of Chemical Engineering and Mechanical Engineering at the California Institute of Technology. He is a fluid mechanician and creator of the Stokesian dynamics method for simulating suspensions of spheres and ellipsoids in low Reynolds number flows. He is an elected fellow of the American Physical Society, a fellow of the Society of Rheology, as well as a member of the National Academy of Sciences, the National Academy of Engineering, and the American Academy of Arts and Sciences.

Hyperuniform materials are characterized by an anomalous suppression of density fluctuations at large scales. More precisely, the vanishing of density fluctuations in the long-wave length limit distinguishes hyperuniform systems from typical gases, liquids, or amorphous solids. Examples of hyperuniformity include all perfect crystals, perfect quasicrystals, and exotic amorphous states of matter.

<span class="mw-page-title-main">Sriram Ramaswamy</span> Indian physicist (born 1957)

Sriram Rajagopal Ramaswamy is an Indian physicist. He is a professor at the Indian Institute of Science, Bangalore, and previously the director of the Tata Institute of Fundamental Research (TIFR) Centre for Interdisciplinary Sciences in Hyderabad.

<span class="mw-page-title-main">M. Cristina Marchetti</span> American physicist

Maria Cristina Marchetti is an Italian-born, American theoretical physicist specializing in statistical physics and condensed matter physics. In 2019, she received the Leo P. Kadanoff Prize of the American Physical Society. She held the William R. Kenan, Jr. Distinguished Professorship of Physics at Syracuse University, where she was the director of the Soft and Living Matter program, and chaired the department 2007–2010. She is currently Professor of Physics at the University of California, Santa Barbara.

<span class="mw-page-title-main">Phase separation</span> Creation of two phases of matter from a single homogenous mixture

Phase separation is the creation of two distinct phases from a single homogeneous mixture. The most common type of phase separation is between two immiscible liquids, such as oil and water. This type of phase separation is known as liquid-liquid equilibrium. Colloids are formed by phase separation, though not all phase separations forms colloids - for example oil and water can form separated layers under gravity rather than remaining as microscopic droplets in suspension.

<span class="mw-page-title-main">Mark Bowick</span> American physicist (born 1957)

Mark John Bowick is a theoretical physicist in condensed matter theory and high energy physics. He is the deputy director of the Kavli Institute for Theoretical Physics at the University of California, Santa Barbara, and a Visiting Distinguished Professor of Physics in UCSB's Physics Department.

Allan Adams is an American physicist and oceanographer. His research in physics has focused on string theory, QFT, and fluid dynamics, while his work in oceanography and ocean engineering have focused on high-precision optical sensing and imaging and on low-cost scalable instrumentation. He currently leads the Future Ocean Lab at Massachusetts Institute of Technology and is a visiting oceanographer at the Woods Hole Oceanographic Institution.

Hartmut Löwen is a German physicist working in the field of statistical mechanics and soft matter physics.

Turbulent phenomena are observed universally in energetic fluid dynamics, associated with highly chaotic fluid motion involving excitations spread over a wide range of length scales. The particular features of turbulence are dependent on the fluid and geometry, and specifics of forcing and dissipation.

References

  1. ↑ Morozov, Alexander (2017-03-24). "From chaos to order in active fluids". Science. 355 (6331): 1262–1263. Bibcode:2017Sci...355.1262M. doi:10.1126/science.aam8998. ISSN   0036-8075. PMID   28336624. S2CID   5238817.
  2. 1 2 3 4 Saintillan, David (2018). "Rheology of Active Fluids". Annual Review of Fluid Mechanics. 50 (1): 563–592. Bibcode:2018AnRFM..50..563S. doi: 10.1146/annurev-fluid-010816-060049 .
  3. ↑ Marchetti, M. C.; Joanny, J. F.; Ramaswamy, S.; Liverpool, T. B.; Prost, J.; Rao, Madan; Simha, R. Aditi (2013-07-19). "Hydrodynamics of soft active matter". Reviews of Modern Physics. 85 (3): 1143–1189. Bibcode:2013RvMP...85.1143M. doi:10.1103/RevModPhys.85.1143.
  4. ↑ Rheology of complex fluids. Deshpande, Abhijit, Y. (Abhijit Yeshwa), Murali Krishnan, J., Sunil Kumar, P. B. New York: Springer. 2010. p. 193. ISBN   9781441964946. OCLC   676699967.{{cite book}}: CS1 maint: others (link)
  5. 1 2 Bratanov, Vasil; Jenko, Frank; Frey, Erwin (2015-12-08). "New class of turbulence in active fluids". Proceedings of the National Academy of Sciences. 112 (49): 15048–15053. Bibcode:2015PNAS..11215048B. doi: 10.1073/pnas.1509304112 . ISSN   0027-8424. PMC   4679023 . PMID   26598708.
  6. ↑ Yeomans, Julia M. (November 2014). "Playful topology". Nature Materials. 13 (11): 1004–1005. Bibcode:2014NatMa..13.1004Y. doi:10.1038/nmat4123. ISSN   1476-4660. PMID   25342530.
  7. 1 2 Yeomans, Julia M. (2017-03-01). "Nature's engines: active matter". Europhysics News. 48 (2): 21–25. Bibcode:2017ENews..48b..21Y. doi: 10.1051/epn/2017204 . ISSN   0531-7479.
  8. ↑ Bonelli, Francesco; Gonnella, Giuseppe; Tiribocchi, Adriano; Marenduzzo, Davide (2016-01-01). "Spontaneous flow in polar active fluids: the effect of a phenomenological self propulsion-like term". The European Physical Journal E. 39 (1): 1. doi:10.1140/epje/i2016-16001-2. ISSN   1292-8941. PMID   26769011. S2CID   5287464.
  9. ↑ Keber, Felix C.; Loiseau, Etienne; Sanchez, Tim; DeCamp, Stephen J.; Giomi, Luca; Bowick, Mark J.; Marchetti, M. Cristina; Dogic, Zvonimir; Bausch, Andreas R. (2014). "Topology and dynamics of active nematic vesicles". Science. 345 (6201): 1135–1139. arXiv: 1409.1836 . Bibcode:2014Sci...345.1135K. doi:10.1126/science.1254784. ISSN   0036-8075. PMC   4401068 . PMID   25190790.
  10. ↑ Marenduzzo, D.; Orlandini, E.; Yeomans, J. M. (2007-03-16). "Hydrodynamics and Rheology of Active Liquid Crystals: A Numerical Investigation". Physical Review Letters. 98 (11): 118102. Bibcode:2007PhRvL..98k8102M. doi:10.1103/PhysRevLett.98.118102. hdl: 11577/1776051 . PMID   17501095.
  11. ↑ Sumino, Yutaka; Nagai, Ken H.; Shitaka, Yuji; Tanaka, Dan; Yoshikawa, Kenichi; Chaté, Hugues; Oiwa, Kazuhiro (March 2012). "Large-scale vortex lattice emerging from collectively moving microtubules" (PDF). Nature. 483 (7390): 448–452. Bibcode:2012Natur.483..448S. doi:10.1038/nature10874. ISSN   1476-4687. PMID   22437613. S2CID   4381568.
  12. ↑ Riedel, Ingmar H.; Kruse, Karsten; Howard, Jonathon (2005-07-08). "A Self-Organized Vortex Array of Hydrodynamically Entrained Sperm Cells". Science. 309 (5732): 300–303. Bibcode:2005Sci...309..300R. doi:10.1126/science.1110329. ISSN   0036-8075. PMID   16002619. S2CID   40668987.
  13. 1 2 Thampi, S. P.; Yeomans, J. M. (2016-07-01). "Active turbulence in active nematics". The European Physical Journal Special Topics. 225 (4): 651–662. arXiv: 1605.00808 . Bibcode:2016EPJST.225..651T. doi:10.1140/epjst/e2015-50324-3. ISSN   1951-6355. S2CID   118487130.
  14. ↑ James, Martin; Wilczek, Michael (2018-02-01). "Vortex dynamics and Lagrangian statistics in a model for active turbulence". The European Physical Journal E. 41 (2): 21. arXiv: 1710.01956 . doi:10.1140/epje/i2018-11625-8. ISSN   1292-8941. PMID   29435676. S2CID   3762381.
  15. ↑ Giomi, Luca; Bowick, Mark J.; Mishra, Prashant; Sknepnek, Rastko; Marchetti, M. Cristina (2014-11-28). "Defect dynamics in active nematics". Phil. Trans. R. Soc. A. 372 (2029): 20130365. arXiv: 1403.5254 . Bibcode:2014RSPTA.37230365G. doi:10.1098/rsta.2013.0365. ISSN   1364-503X. PMC   4223672 . PMID   25332389.
  16. ↑ Elgeti, J.; Cates, M. E.; Marenduzzo, D. (2011-03-22). "Defect hydrodynamics in 2D polar active fluids". Soft Matter. 7 (7): 3177. Bibcode:2011SMat....7.3177E. doi:10.1039/c0sm01097a. ISSN   1744-6848.
  17. 1 2 Großmann, Robert; Romanczuk, Pawel; Bär, Markus; Schimansky-Geier, Lutz (2014-12-19). "Vortex Arrays and Mesoscale Turbulence of Self-Propelled Particles". Physical Review Letters. 113 (25): 258104. arXiv: 1404.7111 . Bibcode:2014PhRvL.113y8104G. doi:10.1103/PhysRevLett.113.258104. PMID   25554911. S2CID   9650798.
  18. ↑ Toner, John; Tu, Yuhai (1998-10-01). "Flocks, herds, and schools: A quantitative theory of flocking". Physical Review E. 58 (4): 4828–4858. arXiv: cond-mat/9804180 . Bibcode:1998PhRvE..58.4828T. doi:10.1103/PhysRevE.58.4828. S2CID   463753.
  19. ↑ Wensink, Henricus H.; Dunkel, Jörn; Heidenreich, Sebastian; Drescher, Knut; Goldstein, Raymond E.; Löwen, Hartmut; Yeomans, Julia M. (2012). "Meso-scale turbulence in living fluids". Proceedings of the National Academy of Sciences. 109 (36): 14308–14313. arXiv: 1208.4239 . Bibcode:2012PNAS..10914308W. doi: 10.1073/pnas.1202032109 . ISSN   0027-8424. PMC   3437854 . PMID   22908244.
  20. ↑ Majumdar, Apala; Cristina, Marchetti M.; Virga, Epifanio G. (2014-11-28). "Perspectives in active liquid crystals". Phil. Trans. R. Soc. A. 372 (2029): 20130373. Bibcode:2014RSPTA.37230373M. doi:10.1098/rsta.2013.0373. ISSN   1364-503X. PMC   4223676 . PMID   25332386.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.