The active reflection coefficient (ARC) is the reflection coefficient for a single antenna element in an array antenna, in the presence of mutual coupling. The active reflection coefficient is a function of frequency in addition to the excitation of the neighboring cells. [1] In computational electromagnetics, the active reflection coefficient is usually determined from unit cell analysis in the frequency domain, where the phase shift over the unit cell (progressive phase shift used to steer the beam) is applied as a boundary condition. It has been suggested that the name "scan reflection coefficient" is more appropriate than "active reflection coefficient", [2] however the latter remains the most commonly used name.
The ARC for antenna element in an array of elements is calculated by: [3]
where are the excitation coefficients and are the coupling coefficients.
In a linear array with inter element spacing , uniform amplitude tapering and scan angle , the following excitation coefficients are used: . By inserting this expression into the general equation above, we obtain: [4]
In antenna theory, a phased array usually means an electronically scanned array, a computer-controlled array of antennas which creates a beam of radio waves that can be electronically steered to point in different directions without moving the antennas.
The propagation constant of a sinusoidal electromagnetic wave is a measure of the change undergone by the amplitude and phase of the wave as it propagates in a given direction. The quantity being measured can be the voltage, the current in a circuit, or a field vector such as electric field strength or flux density. The propagation constant itself measures the change per unit length, but it is otherwise dimensionless. In the context of two-port networks and their cascades, propagation constant measures the change undergone by the source quantity as it propagates from one port to the next.
In electromagnetics, an evanescent field, or evanescent wave, is an oscillating electric and/or magnetic field that does not propagate as an electromagnetic wave but whose energy is spatially concentrated in the vicinity of the source. Even when there is a propagating electromagnetic wave produced, one can still identify as an evanescent field the component of the electric or magnetic field that cannot be attributed to the propagating wave observed at a distance of many wavelengths.
Chebyshev filters are analog or digital filters having a steeper roll-off than Butterworth filters, and have passband ripple or stopband ripple. Chebyshev filters have the property that they minimize the error between the idealized and the actual filter characteristic over the range of the filter, but with ripples in the passband. This type of filter is named after Pafnuty Chebyshev because its mathematical characteristics are derived from Chebyshev polynomials. Type I Chebyshev filters are usually referred to as "Chebyshev filters", while type II filters are usually called "inverse Chebyshev filters".
The Smith chart, invented by Phillip H. Smith (1905–1987) and independently by Mizuhashi Tosaku, is a graphical calculator or nomogram designed for electrical and electronics engineers specializing in radio frequency (RF) engineering to assist in solving problems with transmission lines and matching circuits. The Smith chart can be used to simultaneously display multiple parameters including impedances, admittances, reflection coefficients, scattering parameters, noise figure circles, constant gain contours and regions for unconditional stability, including mechanical vibrations analysis. The Smith chart is most frequently used at or within the unity radius region. However, the remainder is still mathematically relevant, being used, for example, in oscillator design and stability analysis. While the use of paper Smith charts for solving the complex mathematics involved in matching problems has been largely replaced by software based methods, the Smith chart is still a very useful method of showing how RF parameters behave at one or more frequencies, an alternative to using tabular information. Thus most RF circuit analysis software includes a Smith chart option for the display of results and all but the simplest impedance measuring instruments can plot measured results on a Smith chart display.
In telecommunications, particularly in radio frequency, signal strength refers to the transmitter power output as received by a reference antenna at a distance from the transmitting antenna. High-powered transmissions, such as those used in broadcasting, are expressed in dB-millivolts per metre (dBmV/m). For very low-power systems, such as mobile phones, signal strength is usually expressed in dB-microvolts per metre (dBμV/m) or in decibels above a reference level of one milliwatt (dBm). In broadcasting terminology, 1 mV/m is 1000 μV/m or 60 dBμ.
In mathematics and physics, the Christoffel symbols are an array of numbers describing a metric connection. The metric connection is a specialization of the affine connection to surfaces or other manifolds endowed with a metric, allowing distances to be measured on that surface. In differential geometry, an affine connection can be defined without reference to a metric, and many additional concepts follow: parallel transport, covariant derivatives, geodesics, etc. also do not require the concept of a metric. However, when a metric is available, these concepts can be directly tied to the "shape" of the manifold itself; that shape is determined by how the tangent space is attached to the cotangent space by the metric tensor. Abstractly, one would say that the manifold has an associated (orthonormal) frame bundle, with each "frame" being a possible choice of a coordinate frame. An invariant metric implies that the structure group of the frame bundle is the orthogonal group O(p, q). As a result, such a manifold is necessarily a (pseudo-)Riemannian manifold. The Christoffel symbols provide a concrete representation of the connection of (pseudo-)Riemannian geometry in terms of coordinates on the manifold. Additional concepts, such as parallel transport, geodesics, etc. can then be expressed in terms of Christoffel symbols.
In electromagnetics, directivity is a parameter of an antenna or optical system which measures the degree to which the radiation emitted is concentrated in a single direction. It is the ratio of the radiation intensity in a given direction from the antenna to the radiation intensity averaged over all directions. Therefore, the directivity of a hypothetical isotropic radiator is 1, or 0 dBi.
The Wigner D-matrix is a unitary matrix in an irreducible representation of the groups SU(2) and SO(3). The complex conjugate of the D-matrix is an eigenfunction of the Hamiltonian of spherical and symmetric rigid rotors. The matrix was introduced in 1927 by Eugene Wigner. D stands for Darstellung, which means "representation" in German.
Fluorescence interference contrast (FLIC) microscopy is a microscopic technique developed to achieve z-resolution on the nanometer scale.
The Prandtl lifting-line theory is a mathematical model that predicts lift distribution over a three-dimensional wing based on its geometry. It is also known as the Lanchester–Prandtl wing theory.
The UNIFAC method is a semi-empirical system for the prediction of non-electrolyte activity in non-ideal mixtures. UNIFAC uses the functional groups present on the molecules that make up the liquid mixture to calculate activity coefficients. By using interactions for each of the functional groups present on the molecules, as well as some binary interaction coefficients, the activity of each of the solutions can be calculated. This information can be used to obtain information on liquid equilibria, which is useful in many thermodynamic calculations, such as chemical reactor design, and distillation calculations.
Wi-Fi positioning system is a geolocation system that uses the characteristics of nearby Wi-Fi hotspots and other wireless access points to discover where a device is located.
A signal travelling along an electrical transmission line will be partly, or wholly, reflected back in the opposite direction when the travelling signal encounters a discontinuity in the characteristic impedance of the line, or if the far end of the line is not terminated in its characteristic impedance. This can happen, for instance, if two lengths of dissimilar transmission lines are joined together.
The table of chords, created by the Greek astronomer, geometer, and geographer Ptolemy in Egypt during the 2nd century AD, is a trigonometric table in Book I, chapter 11 of Ptolemy's Almagest, a treatise on mathematical astronomy. It is essentially equivalent to a table of values of the sine function. It was the earliest trigonometric table extensive enough for many practical purposes, including those of astronomy. Centuries passed before more extensive trigonometric tables were created. One such table is the Canon Sinuum created at the end of the 16th century.
A synchronization network is a network of coupled dynamical systems. It consists of a network connecting oscillators, where oscillators are nodes that emit a signal with somewhat regular frequency, and are also capable of receiving a signal.
The total active reflection coefficient (TARC) within mathematics and physics scattering theory, relates the total incident power to the total outgoing power in an N-port microwave component. The TARC is mainly used for multiple-input multiple-output (MIMO) antenna systems and array antennas, where the outgoing power is unwanted reflected power. The name shows the similarities with the active reflection coefficient, which is used for single elements. The TARC is the square root of the sum of all outgoing powers at the ports, divided by the sum of all incident powers at the ports of an N-port antenna. Similarly to the active reflection coefficient, the TARC is a function of frequency, and it also depends on scan angle and tapering. With this definition we can characterize the multi-port antenna’s frequency bandwidth and radiation performance. When the antennas are made of lossless materials, TARC can be computed directly from the scattering matrix by
The two-rays ground-reflection model is a multipath radio propagation model which predicts the path losses between a transmitting antenna and a receiving antenna when they are in line of sight (LOS). Generally, the two antenna each have different height. The received signal having two components, the LOS component and the reflection component formed predominantly by a single ground reflected wave.
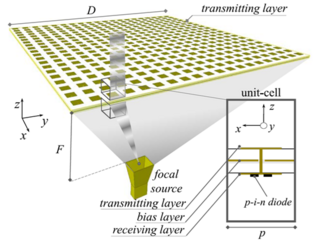
A transmitarray antenna is a phase-shifting surface (PSS), a structure capable of focusing electromagnetic radiation from a source antenna to produce a high-gain beam. Transmitarrays consist of an array of unit cells placed above a source (feeding) antenna. Phase shifts are applied to the unit cells, between elements on the receive and transmit surfaces, to focus the incident wavefronts from the feeding antenna. These thin surfaces can be used instead of a dielectric lens. Unlike phased arrays, transmitarrays do not require a feed network, so losses can be greatly reduced. Similarly, they have an advantage over reflectarrays in that feed blockage is avoided.
