Related Research Articles

Financial economics is the branch of economics characterized by a "concentration on monetary activities", in which "money of one type or another is likely to appear on both sides of a trade". Its concern is thus the interrelation of financial variables, such as share prices, interest rates and exchange rates, as opposed to those concerning the real economy. It has two main areas of focus: asset pricing and corporate finance; the first being the perspective of providers of capital, i.e. investors, and the second of users of capital. It thus provides the theoretical underpinning for much of finance.
Volatility risk is the risk of an adverse change of price, due to changes in the volatility of a factor affecting that price. It usually applies to derivative instruments, and their portfolios, where the volatility of the underlying asset is a major influencer of option prices. It is also relevant to portfolios of basic assets, and to foreign currency trading.

A short-rate model, in the context of interest rate derivatives, is a mathematical model that describes the future evolution of interest rates by describing the future evolution of the short rate, usually written .
In financial mathematics, the Hull–White model is a model of future interest rates. In its most generic formulation, it belongs to the class of no-arbitrage models that are able to fit today's term structure of interest rates. It is relatively straightforward to translate the mathematical description of the evolution of future interest rates onto a tree or lattice and so interest rate derivatives such as bermudan swaptions can be valued in the model.
Monte Carlo methods are used in corporate finance and mathematical finance to value and analyze (complex) instruments, portfolios and investments by simulating the various sources of uncertainty affecting their value, and then determining the distribution of their value over the range of resultant outcomes. This is usually done by help of stochastic asset models. The advantage of Monte Carlo methods over other techniques increases as the dimensions of the problem increase.
John C. Hull is a professor of Derivatives and Risk Management at the Rotman School of Management at the University of Toronto.
In finance, a bond option is an option to buy or sell a bond at a certain price on or before the option expiry date. These instruments are typically traded OTC.
In financial economics, asset pricing refers to a formal treatment and development of two interrelated pricing principles, outlined below, together with the resultant models. There have been many models developed for different situations, but correspondingly, these stem from either general equilibrium asset pricing or rational asset pricing, the latter corresponding to risk neutral pricing.
Financial modeling is the task of building an abstract representation of a real world financial situation. This is a mathematical model designed to represent the performance of a financial asset or portfolio of a business, project, or any other investment.
In mathematical finance, the Black–Derman–Toy model (BDT) is a popular short-rate model used in the pricing of bond options, swaptions and other interest rate derivatives; see Lattice model (finance) § Interest rate derivatives. It is a one-factor model; that is, a single stochastic factor—the short rate—determines the future evolution of all interest rates. It was the first model to combine the mean-reverting behaviour of the short rate with the log-normal distribution, and is still widely used.
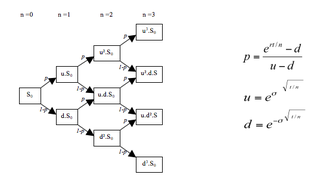
In finance, a lattice model is a mathematical approach to the valuation of derivatives in situations requiring a discrete time model. For dividend paying equity options, a typical application would correspond to the pricing of an American-style option, where a decision to exercise is allowed at any time up to the maturity. A continuous model, on the other hand, such as the standard Black–Scholes one, would only allow for the valuation of European options, where exercise is limited to the option's maturity date. For interest rate derivatives lattices are additionally useful in that they address many of the issues encountered with continuous models, such as pull to par. The method is also used for valuing certain exotic options, because of path dependence in the payoff. Traditional Monte Carlo methods for option pricing fail to account for optimal decisions to terminate the derivative by early exercise, but some methods now exist for solving this problem.
The following outline is provided as an overview of and topical guide to finance:
In finance, the Chen model is a mathematical model describing the evolution of interest rates. It is a type of "three-factor model" as it describes interest rate movements as driven by three sources of market risk. It was the first stochastic mean and stochastic volatility model and it was published in 1994 by Lin Chen, economist, theoretical physicist and former lecturer/professor at Beijing Institute of Technology, American University of Beirut, Yonsei University of Korea, and SunYetSan University.
The Rendleman–Bartter model in finance is a short-rate model describing the evolution of interest rates. It is a "one factor model" as it describes interest rate movements as driven by only one source of market risk. It can be used in the valuation of interest rate derivatives. It is a stochastic asset model.
In finance, an option is a contract which conveys to its owner, the holder, the right, but not the obligation, to buy or sell a specific quantity of an underlying asset or instrument at a specified strike price on or before a specified date, depending on the style of the option.
Damiano Brigo is a mathematician known for research in mathematical finance, filtering theory, stochastic analysis with differential geometry, probability theory and statistics, authoring more than 130 research publications and three monographs. From 2012 he serves as full professor with a chair in mathematical finance at the Department of Mathematics of Imperial College London, where he headed the Mathematical Finance group in 2012–2019. He is also a well known quantitative finance researcher, manager and advisor in the industry. His research has been cited and published also in mainstream industry publications, including Risk Magazine, where he has been the most cited author in the twenty years 1998–2017. He is often requested as a plenary or invited speaker both at academic and industry international events. Brigo's research has also been used in court as support for legal proceedings.
Eduardo Saul Schwartz is a professor of finance at SFU's Beedie School of Business, where he holds the Ryan Beedie Chair in Finance. He is also a Distinguished Research Professor at the University of California, Los Angeles. He is known for pioneering research in several areas of finance, particularly derivatives. His major contributions include: the real options method of pricing investments under uncertainty; the Longstaff–Schwartz model - a multi-factor short-rate model; the Longstaff-Schwartz method for valuing American options by Monte Carlo Simulation; the use of Finite difference methods for option pricing.
Quantitative analysis is the use of mathematical and statistical methods in finance and investment management. Those working in the field are quantitative analysts (quants). Quants tend to specialize in specific areas which may include derivative structuring or pricing, risk management, investment management and other related finance occupations. The occupation is similar to those in industrial mathematics in other industries. The process usually consists of searching vast databases for patterns, such as correlations among liquid assets or price-movement patterns.
Mathematical finance, also known as quantitative finance and financial mathematics, is a field of applied mathematics, concerned with mathematical modeling in the financial field.