Allen's interval algebra

For the type of boolean algebra called interval algebra, see Boolean algebra (structure) § Examples.

Allen's interval algebra is a calculus for temporal reasoning that was introduced by James F. Allen in 1983.

The calculus defines possible relations between time intervals and provides a composition table that can be used as a basis for reasoning about temporal descriptions of events.

Formal description

Relations

The following 13 base relations capture the possible relations between two intervals.

Relation	Illustration	Interpretation
${\displaystyle X\,{\mathrel {\mathbf {<} }}\,Y}$ ${\displaystyle Y\,{\mathrel {\mathbf {>} }}\,X}$		X precedes Y Y is preceded by X
${\displaystyle X\,{\mathrel {\mathbf {m} }}\,Y}$ ${\displaystyle Y\,{\mathrel {\mathbf {mi} }}\,X}$		X meets Y Y is met by X (i stands for inverse)
${\displaystyle X\,{\mathrel {\mathbf {o} }}\,Y}$ ${\displaystyle Y\,{\mathrel {\mathbf {oi} }}\,X}$		X overlaps with Y Y is overlapped by X
${\displaystyle X\,{\mathrel {\mathbf {s} }}\,Y}$ ${\displaystyle Y\,{\mathrel {\mathbf {si} }}\,X}$		X starts Y Y is started by X
${\displaystyle X\,{\mathrel {\mathbf {d} }}\,Y}$ ${\displaystyle Y\,{\mathrel {\mathbf {di} }}\,X}$		X during Y Y contains X
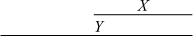${\displaystyle X\,{\mathrel {\mathbf {f} }}\,Y}$ ${\displaystyle Y\,{\mathrel {\mathbf {fi} }}\,X}$		X finishes Y Y is finished by X
${\displaystyle X\,{\mathrel {\mathbf {=} }}\,Y}$		X is equal to Y

To see that the 13 relations are exhaustive, note that each point of ${\displaystyle X}$ can be at 5 possible locations relative to ${\displaystyle Y}$: before, at the start, within, at the end, after. These give ${\displaystyle 5+4+3+2+1=15}$ possible relative positions for the start and the end of ${\displaystyle X}$. Of these, we cannot have ${\displaystyle X_{0}=X_{1}=Y_{0}}$ since ${\displaystyle X_{0}<X_{1}}$, and similarly we cannot have ${\displaystyle X_{0}=X_{1}=Y_{1}}$, thus giving us 13 possible relations.

In general, the number of different relations between n intervals, starting with n = 0, is 1, 1, 13, 409, 23917, 2244361... OEIS A055203. The special case shown above is for n = 2.

Composition of relations between intervals

For reasoning about the relations between temporal intervals, Allen's interval algebra provides a composition table. Given the relation between ${\displaystyle X}$ and ${\displaystyle Y}$ and the relation between ${\displaystyle Y}$ and ${\displaystyle Z}$, the composition table allows for concluding about the relation between ${\displaystyle X}$ and ${\displaystyle Z}$. Together with a converse operation, this turns Allen's interval algebra into a relation algebra.

Using this calculus, given facts can be formalized and then used for automatic reasoning. Relations between intervals are formalized as sets of base relations.

The sentences

During dinner, Peter reads the newspaper. Afterwards, he goes to bed.

are formalized in Allen's Interval Algebra as follows:

${\displaystyle {\mbox{newspaper }}\mathbf {\{\operatorname {d} \}} {\mbox{ dinner}}}$

${\displaystyle {\mbox{dinner }}\mathbf {\{\operatorname {<} \}} {\mbox{ bed}}}$

For the example, one can infer ${\displaystyle {\mbox{newspaper }}\mathbf {\{\operatorname {<} \}} {\mbox{ bed}}}$.

Extensions

Allen's interval algebra can be used for the description of both temporal intervals and spatial configurations. For the latter use, the relations are interpreted as describing the relative position of spatial objects. This also works for three-dimensional objects by listing the relation for each coordinate separately.

The study of overlapping markup uses a similar algebra (see ^[1] ). Its models have more variations depending on whether endpoints of document structures are permitted to be truly co-located, or merely [tangent].

Temporal primitives

In the cultural heritage ontology CIDOC CRM, Allen relations are replaced by so-called temporal primitives, which facilitate the formulation of attestable statements as well as reasoning about these statements. ^[2] Temporal primitives split up the Allen relations into individual statements about the start or end of the intervals. For example, X overlaps with Y (${\displaystyle X\mathbf {\operatorname {o} } Y}$) can be split as follows:

• ${\displaystyle X\mathbf {\operatorname {o} } Y}$ ⇔ starts before the start of (${\displaystyle X}$,${\displaystyle Y}$) ∧ ends after the start of (${\displaystyle X}$,${\displaystyle Y}$) ∧ ends before the end of (${\displaystyle X}$,${\displaystyle Y}$)

In addition, the equal to of the Allen relations is replaced by before or with and after or with. A simple example:

• The reign of King Harold II starts before the start of the Battle of Hastings
• The reign/life of Harold II ends after or with the start of the Battle of Hastings
• The reign/life of Harold II ends before or with the end of the Battle of Hastings

In the example, it is not necessary to specify whether Harold II was killed at the beginning or during or at the end of the battle, i.e. whether ${\displaystyle X\mathbf {\operatorname {m} } Y}$, ${\displaystyle X\mathbf {\operatorname {o} } Y}$ or ${\displaystyle X\mathbf {\operatorname {fi} } Y}$ applies (disjunctions such as ${\displaystyle \mathbf {\{\operatorname {m} ,\operatorname {o} ,\operatorname {fi} \}} }$ cannot be expressed in CIDOC CRM, except in queries). If it is relevant for a particular historical question, it can be specified later by adding e.g. ends after the start of.

CIDOC CRM distinguishes between events and their corresponding time intervals. Allen relations and temporal primitives are statements between events and only as a consequence between their time intervals. Another difference is that temporal, spatial and spatiotemporal entities in CIDOC CRM are seen as having fuzzy borders. Especially statements about exact simultaneity are otherwise extremely rare.

Implementations

• A simple java library implementing the concept of Allen's temporal relations and the path consistency algorithm
• Java library implementing Allen's Interval Algebra (incl. data and index structures, e.g., interval tree)
• OWL-Time Time Ontology in OWL an OWL-2 DL ontology of temporal concepts, for describing the temporal properties of resources in the world or described in Web pages.
• GQR is a reasoner for Allen's interval algebra (and many others)
• qualreas is a Python framework for qualitative reasoning over networks of relation algebras, such as RCC-8, Allen's interval algebra, and Allen's algebra integrated with Time Points and situated in either Left- or Right-Branching Time.
• SparQ is a reasoner for Allen's interval algebra (and many others)
• EveXL is a small domain-specific language for the detection of events that implements the Interval Algebra's operators via ASCII art patterns.

See also

• Temporal logic
• Logic
• Region connection calculus
• Spatial relation (analog)
• Commonsense reasoning

References

1. Steven DeRose. Markup Overlap: A Review and a Horse. In Proceedings of Extreme Markup Languages 2004, Montréal, Québec, August 2-6, 2004. http://xml.coverpages.org/DeRoseEML2004.pdf
2. CIDOC CRM Version 7.3: https://cidoc-crm.org/versions-of-the-cidoc-crm, section Temporal Relation Primitives based on fuzzy boundaries

Sources

• Allen, James F. (26 November 1983). "Maintaining knowledge about temporal intervals" (PDF). Communications of the ACM. 26 (11): 832–843. CiteSeerX   10.1.1.472.5244 . doi:10.1145/182.358434. hdl:1802/10574. ISSN   0001-0782. S2CID   16729000.
• Nebel, Bernhard; Bürckert, Hans-Jürgen (1995). "Reasoning about Temporal Relations: A Maximal Tractable Subclass of Allen's Interval Algebra" (PDF). Journal of the ACM. 42: 43–66. doi: 10.1145/200836.200848 . S2CID   6586759.
• van Beek, Peter; Manchak, Dennis W. (1996). "The design and experimental analysis of algorithms for temporal reasoning" (PDF). Journal of Artificial Intelligence Research. 4 (1996): 1–18. arXiv: cs/9601101 . Bibcode:1996cs........1101V. doi:10.1613/jair.232. S2CID   3204600. Archived from the original (PDF) on 6 July 2017. Retrieved 6 May 2017.