Alternating factorial

Last updated April 03, 2024

In mathematics, an alternating factorial is the absolute value of the alternating sum of the first n factorials of positive integers.

This is the same as their sum, with the odd-indexed factorials multiplied by −1 if n is even, and the even-indexed factorials multiplied by −1 if n is odd, resulting in an alternation of signs of the summands (or alternation of addition and subtraction operators, if preferred). To put it algebraically,

\operatorname {af} (n)=\sum _{i=1}^{n}(-1)^{n-i}i!

or with the recurrence relation

\operatorname {af} (n)=n!-\operatorname {af} (n-1)

in which af(1) = 1.

The first few alternating factorials are

1, 1, 5, 19, 101, 619, 4421, 35899, 326981, 3301819, 36614981, 442386619, 5784634181, 81393657019 (sequence A005165 in the OEIS )

For example, the third alternating factorial is 1! – 2! + 3!. The fourth alternating factorial is −1! + 2! − 3! + 4! = 19. Regardless of the parity of n, the last (nth) summand, n!, is given a positive sign, the (n – 1)th summand is given a negative sign, and the signs of the lower-indexed summands are alternated accordingly.

This pattern of alternation ensures the resulting sums are all positive integers. Changing the rule so that either the odd- or even-indexed summands are given negative signs (regardless of the parity of n) changes the signs of the resulting sums but not their absolute values.

Živković (1999) proved that there are only a finite number of alternating factorials that are also prime numbers, since 3612703 divides af(3612702) and therefore divides af(n) for all n≥ 3612702.^[1]As of 2024^[update], the known primes and probable primes are af(n) for (sequence A001272 in the OEIS )

n = 3, 4, 5, 6, 7, 8, 10, 15, 19, 41, 59, 61, 105, 160, 661, 2653, 3069, 3943, 4053, 4998, 8275, 9158, 11164, 43592, 59961

Only the values up to n = 661 have been proved prime in 2006. af(661) is approximately 7.818097272875 × 10¹⁵⁷⁸.

Notes

↑ Živković (1999).

Related Research Articles

In mathematics, the Bernoulli numbers $B n$ are a sequence of rational numbers which occur frequently in analysis. The Bernoulli numbers appear in the Taylor series expansions of the tangent and hyperbolic tangent functions, in Faulhaber's formula for the sum of m-th powers of the first n positive integers, in the Euler–Maclaurin formula, and in expressions for certain values of the Riemann zeta function.

In mathematics, the factorial of a non-negative integer $,$ denoted by $,$ is the product of all positive integers less than or equal to $.$ The factorial of also equals the product of $with the next smaller factorial:$

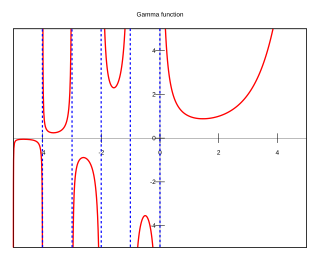
In mathematics, the gamma function is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For every positive integer $n$ ,

In mathematics, a series is, roughly speaking, the operation of adding infinitely many quantities, one after the other, to a given starting quantity. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathematics, even for studying finite structures through generating functions. In addition to their ubiquity in mathematics, infinite series are also widely used in other quantitative disciplines such as physics, computer science, statistics and finance.

In mathematics, the Euler numbers are a sequence E_n of integers defined by the Taylor series expansion

In mathematics, an infinite series of numbers is said to converge absolutely if the sum of the absolute values of the summands is finite. More precisely, a real or complex series $is said to converge absolutely if for some real number Similarly, an improper integral of a function, is said to converge absolutely if the integral of the absolute value of the integrand is finite—that is, if$

10 (ten) is the even natural number following 9 and preceding 11. Ten is the base of the decimal numeral system, the most common system of denoting numbers in both spoken and written language.

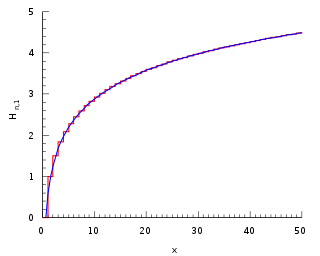
<span class="mw-page-title-main">Harmonic number</span> Sum of the first n whole number reciprocals; 1/1 + 1/2 + 1/3 + ... + 1/n

In mathematics, the $n$ -th harmonic number is the sum of the reciprocals of the first $n$ natural numbers:

In mathematics, summation is the addition of a sequence of numbers, called addends or summands; the result is their sum or total. Beside numbers, other types of values can be summed as well: functions, vectors, matrices, polynomials and, in general, elements of any type of mathematical objects on which an operation denoted "+" is defined.

The sum of the reciprocals of all prime numbers diverges; that is:

63 (sixty-three) is the natural number following 62 and preceding 64.

In mathematics, and more particularly in number theory, primorial, denoted by "#", is a function from natural numbers to natural numbers similar to the factorial function, but rather than successively multiplying positive integers, the function only multiplies prime numbers.

In mathematics, the double factorial of a number $n$ , denoted by $n ‼$ , is the product of all the positive integers up to $n$ that have the same parity as $n$ . That is,

In mathematics, the Iverson bracket, named after Kenneth E. Iverson, is a notation that generalises the Kronecker delta, which is the Iverson bracket of the statement $x = y$ . It maps any statement to a function of the free variables in that statement. This function is defined to take the value 1 for the values of the variables for which the statement is true, and takes the value 0 otherwise. It is generally denoted by putting the statement inside square brackets:

In mathematics, the Riemann series theorem, also called the Riemann rearrangement theorem, named after 19th-century German mathematician Bernhard Riemann, says that if an infinite series of real numbers is conditionally convergent, then its terms can be arranged in a permutation so that the new series converges to an arbitrary real number, or diverges. This implies that a series of real numbers is absolutely convergent if and only if it is unconditionally convergent.

In mathematics, the Riemann zeta function is a function in complex analysis, which is also important in number theory. It is often denoted $and is named after the mathematician Bernhard Riemann. When the argument is a real number greater than one, the zeta function satisfies the equation$

5 (five) is a number, numeral and digit. It is the natural number, and cardinal number, following 4 and preceding 6, and is a prime number. It has garnered attention throughout history in part because distal extremities in humans typically contain five digits.

In mathematics, the sophomore's dream is the pair of identities

Multiplicative partitions of factorials are expressions of values of the factorial function as products of powers of prime numbers. They have been studied by Paul Erdős and others.

References

Weisstein, Eric W. "Alternating Factorial". MathWorld .
Živković, Miodrag (1999). "The number of primes ${\textstyle \sum _{i=1}^{n}(-1)^{n-i}i!}$ is finite". Mathematics of Computation . 68 (225). American Mathematical Society: 403–409. Bibcode:1999MaCom..68..403Z. doi:10.1090/S0025-5718-99-00990-4.
Yves Gallot, Is the number of primes ${\textstyle {1 \over 2}\sum _{i=0}^{n-1}i!}$ finite?
Paul Jobling, Guy's problem B43: search for primes of form n!-(n-1)!+(n-2)!-(n-3)!+...+/-1!

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[FOOTNOTEŽivković1999-1] Živković (1999).

[1]