The statcoulomb (statC), franklin (Fr), or electrostatic unit of charge (esu) is the unit of measurement for electrical charge used in the centimetre–gram–second electrostatic units variant (CGS-ESU) and Gaussian systems of units. It is a derived unit given by
In electrochemistry, the Nernst equation is a chemical thermodynamical relationship that permits the calculation of the reduction potential of a reaction from the standard electrode potential, absolute temperature, the number of electrons involved in the redox reaction, and activities of the chemical species undergoing reduction and oxidation respectively. It was named after Walther Nernst, a German physical chemist who formulated the equation.

In mathematics and physics, the heat equation is a certain partial differential equation. Solutions of the heat equation are sometimes known as caloric functions. The theory of the heat equation was first developed by Joseph Fourier in 1822 for the purpose of modeling how a quantity such as heat diffuses through a given region. Since then, the heat equation and its variants have been found to be fundamental in many parts of both pure and applied mathematics.
Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the differentiation operator
Space charge is an interpretation of a collection of electric charges in which excess electric charge is treated as a continuum of charge distributed over a region of space rather than distinct point-like charges. This model typically applies when charge carriers have been emitted from some region of a solid—the cloud of emitted carriers can form a space charge region if they are sufficiently spread out, or the charged atoms or molecules left behind in the solid can form a space charge region.
A continuity equation or transport equation is an equation that describes the transport of some quantity. It is particularly simple and powerful when applied to a conserved quantity, but it can be generalized to apply to any extensive quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described using continuity equations.
In solid-state physics, the electron mobility characterises how quickly an electron can move through a metal or semiconductor when pushed or pulled by an electric field. There is an analogous quantity for holes, called hole mobility. The term carrier mobility refers in general to both electron and hole mobility.

In electrochemistry, cyclic voltammetry (CV) is a type of voltammetric measurement where the potential of the working electrode is ramped linearly versus time. Unlike in linear sweep voltammetry, after the set potential is reached in a CV experiment, the working electrode's potential is ramped in the opposite direction to return to the initial potential. These cycles in potential are repeated until the voltammetric trace reaches a cyclic steady state. The current at the working electrode is plotted versus the voltage at the working electrode to yield the cyclic voltammogram. Cyclic voltammetry is generally used to study the electrochemical properties of an analyte in solution or of a molecule that is adsorbed onto the electrode.
The Goldman–Hodgkin–Katz voltage equation, sometimes called the Goldman equation, is used in cell membrane physiology to determine the resting potential across a cell's membrane, taking into account all of the ions that are permeant through that membrane.

Voltammetry is a category of electroanalytical methods used in analytical chemistry and various industrial processes. In voltammetry, information about an analyte is obtained by measuring the current as the potential is varied. The analytical data for a voltammetric experiment comes in the form of a voltammogram, which plots the current produced by the analyte versus the potential of the working electrode.
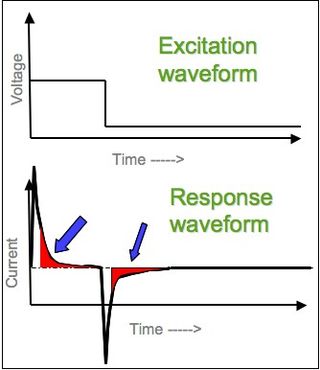
In electrochemistry, chronoamperometry is an analytical technique in which the electric potential of the working electrode is stepped and the resulting current from faradaic processes occurring at the electrode is monitored as a function of time. The functional relationship between current response and time is measured after applying single or double potential step to the working electrode of the electrochemical system. Limited information about the identity of the electrolyzed species can be obtained from the ratio of the peak oxidation current versus the peak reduction current. However, as with all pulsed techniques, chronoamperometry generates high charging currents, which decay exponentially with time as any RC circuit. The Faradaic current - which is due to electron transfer events and is most often the current component of interest - decays as described in the Cottrell equation. In most electrochemical cells, this decay is much slower than the charging decay-cells with no supporting electrolyte are notable exceptions. Most commonly a three-electrode system is used. Since the current is integrated over relatively longer time intervals, chronoamperometry gives a better signal-to-noise ratio in comparison to other amperometric techniques.
In physics, the Einstein relation is a previously unexpected connection revealed independently by William Sutherland in 1904, Albert Einstein in 1905, and by Marian Smoluchowski in 1906 in their works on Brownian motion. The more general form of the equation in the classical case is
Polarography is a type of voltammetry where the working electrode is a dropping mercury electrode (DME) or a static mercury drop electrode (SMDE), which are useful for their wide cathodic ranges and renewable surfaces. It was invented in 1922 by Czechoslovak chemist Jaroslav Heyrovský, for which he won the Nobel prize in 1959. The main advantages of mercury as electrode material are as follows: 1) a large voltage window: ca. from +0.2 V to -1.8 V vs reversible hydrogen electrode (RHE). Hg electrode is particularly well-suited for studying electroreduction reactions. 2) very reproducible electrode surface, since mercury is liquid. 3) very easy cleaning of the electrode surface by making a new drop of mercury from a large Hg pool connected by a glass capillary.
Diffusivity, mass diffusivity or diffusion coefficient is usually written as the proportionality constant between the molar flux due to molecular diffusion and the negative value of the gradient in the concentration of the species. More accurately, the diffusion coefficient times the local concentration is the proportionality constant between the negative value of the mole fraction gradient and the molar flux. This distinction is especially significant in gaseous systems with strong temperature gradients. Diffusivity derives its definition from Fick's law and plays a role in numerous other equations of physical chemistry.

In electrochemistry, the Cottrell equation describes the change in electric current with respect to time in a controlled potential experiment, such as chronoamperometry. Specifically it describes the current response when the potential is a step function in time. It was derived by Frederick Gardner Cottrell in 1903. For a simple redox event, such as the ferrocene/ferrocenium couple, the current measured depends on the rate at which the analyte diffuses to the electrode. That is, the current is said to be "diffusion controlled". The Cottrell equation describes the case for an electrode that is planar but can also be derived for spherical, cylindrical, and rectangular geometries by using the corresponding Laplace operator and boundary conditions in conjunction with Fick's second law of diffusion.
In electrochemistry, the Butler–Volmer equation, also known as Erdey-Grúz–Volmer equation, is one of the most fundamental relationships in electrochemical kinetics. It describes how the electrical current through an electrode depends on the voltage difference between the electrode and the bulk electrolyte for a simple, unimolecular redox reaction, considering that both a cathodic and an anodic reaction occur on the same electrode:
The Levich equation models the diffusion and solution flow conditions around a rotating disk electrode (RDE). It is named after Veniamin Grigorievich Levich who first developed an RDE as a tool for electrochemical research. It can be used to predict the current observed at an RDE, in particular, the Levich equation gives the height of the sigmoidal wave observed in rotating disk voltammetry. The sigmoidal wave height is often called the Levich current.
In electrochemistry, the Randles–Ševčík equation describes the effect of scan rate on the peak current for a cyclic voltammetry experiment. For simple redox events where the reaction is electrochemically reversible, and the products and reactants are both soluble, such as the ferrocene/ferrocenium couple, ip depends not only on the concentration and diffusional properties of the electroactive species but also on scan rate.
A Levich constant (B) is often used in order to simplify the Levich equation. Furthermore, B is readily extracted from rotating disk electrode experimental data.
In electrochemistry, the Berzins-Delahay equation is analogous to the Randles–Sevcik equation, except that it predicts the peak height of a linear potential scan when the reaction is electrochemically reversible, the reactants are soluble, and the products are deposited on the electrode with a thermodynamic activity of one.






