Related Research Articles
Knowledge representation and reasoning is the field of artificial intelligence (AI) dedicated to representing information about the world in a form that a computer system can use to solve complex tasks such as diagnosing a medical condition or having a dialog in a natural language. Knowledge representation incorporates findings from psychology about how humans solve problems and represent knowledge in order to design formalisms that will make complex systems easier to design and build. Knowledge representation and reasoning also incorporates findings from logic to automate various kinds of reasoning, such as the application of rules or the relations of sets and subsets.

In geometry and physics, spinors are elements of a complex vector space that can be associated with Euclidean space. Like geometric vectors and more general tensors, spinors transform linearly when the Euclidean space is subjected to a slight (infinitesimal) rotation. However, when a sequence of such small rotations is composed (integrated) to form an overall final rotation, the resulting spinor transformation depends on which sequence of small rotations was used. Unlike vectors and tensors, a spinor transforms to its negative when the space is continuously rotated through a complete turn from 0° to 360°. This property characterizes spinors: spinors can be viewed as the "square roots" of vectors.
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π(g) is a unitary operator for every g ∈ G. The general theory is well-developed in case G is a locally compact (Hausdorff) topological group and the representations are strongly continuous.

In mathematics, a simple Lie group is a connected non-abelian Lie group G which does not have nontrivial connected normal subgroups. The list of simple Lie groups can be used to read off the list of simple Lie algebras and Riemannian symmetric spaces.

In mathematics, G2 is the name of three simple Lie groups (a complex form, a compact real form and a split real form), their Lie algebras as well as some algebraic groups. They are the smallest of the five exceptional simple Lie groups. G2 has rank 2 and dimension 14. It has two fundamental representations, with dimension 7 and 14.

In mathematics, F4 is the name of a Lie group and also its Lie algebra f4. It is one of the five exceptional simple Lie groups. F4 has rank 4 and dimension 52. The compact form is simply connected and its outer automorphism group is the trivial group. Its fundamental representation is 26-dimensional.

In mathematics, E6 is the name of some closely related Lie groups, linear algebraic groups or their Lie algebras , all of which have dimension 78; the same notation E6 is used for the corresponding root lattice, which has rank 6. The designation E6 comes from the Cartan–Killing classification of the complex simple Lie algebras (see Élie Cartan § Work). This classifies Lie algebras into four infinite series labeled An, Bn, Cn, Dn, and five exceptional cases labeled E6, E7, E8, F4, and G2. The E6 algebra is thus one of the five exceptional cases.
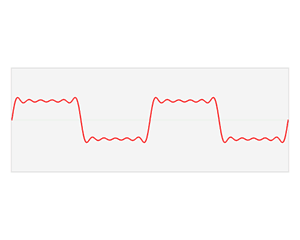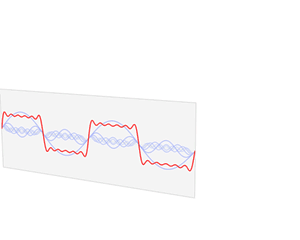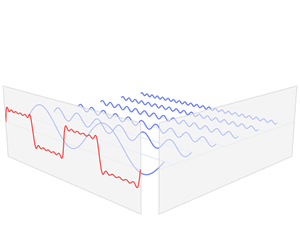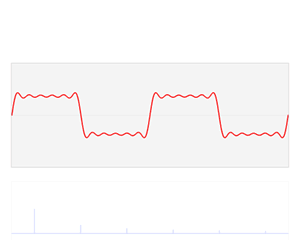
In physics, electronics, control systems engineering, and statistics, the frequency domain refers to the analysis of mathematical functions or signals with respect to frequency, rather than time. Put simply, a time-domain graph shows how a signal changes over time, whereas a frequency-domain graph shows how much of the signal lies within each given frequency band over a range of frequencies. A frequency-domain representation can also include information on the phase shift that must be applied to each sinusoid in order to be able to recombine the frequency components to recover the original time signal.
In mathematics, an invariant subspace of a linear mapping T : V → V from some vector space V to itself, is a subspace W of V that is preserved by T; that is, T(W) ⊆ W.

In mathematics, E7 is the name of several closely related Lie groups, linear algebraic groups or their Lie algebras e7, all of which have dimension 133; the same notation E7 is used for the corresponding root lattice, which has rank 7. The designation E7 comes from the Cartan–Killing classification of the complex simple Lie algebras, which fall into four infinite series labeled An, Bn, Cn, Dn, and five exceptional cases labeled E6, E7, E8, F4, and G2. The E7 algebra is thus one of the five exceptional cases.
In representation theory of Lie groups and Lie algebras, a fundamental representation is an irreducible finite-dimensional representation of a semisimple Lie group or Lie algebra whose highest weight is a fundamental weight. For example, the defining module of a classical Lie group is a fundamental representation. Any finite-dimensional irreducible representation of a semisimple Lie group or Lie algebra can be constructed from the fundamental representations by a procedure due to Élie Cartan. Thus in a certain sense, the fundamental representations are the elementary building blocks for arbitrary finite-dimensional representations.
In mathematics, a complex representation is a representation of a group on a complex vector space. Sometimes, the term complex representation is reserved for a representation on a complex vector space that is neither real nor pseudoreal (quaternionic). In other words, the group elements are expressed as complex matrices, and the complex conjugate of a complex representation is a different, non-equivalent representation. For compact groups, the Frobenius-Schur indicator can be used to tell whether a representation is real, complex, or pseudo-real.
In the mathematical field of representation theory a real representation is usually a representation on a real vector space U, but it can also mean a representation on a complex vector space V with an invariant real structure, i.e., an antilinear equivariant map
In harmonic analysis and number theory, an automorphic form is a well-behaved function from a topological group G to the complex numbers which is invariant under the action of a discrete subgroup of the topological group. Automorphic forms are a generalization of the idea of periodic functions in Euclidean space to general topological groups.

This article gives a table of some common Lie groups and their associated Lie algebras.
A conceptual model is a representation of a system. It consists of concepts used to help people know, understand, or simulate a subject the model represents. It is also a set of concepts. In contrast, physical models are physical objects, such as a toy model that may be assembled and made to work like the object it represents.
In mathematics, a matrix group is a group G consisting of invertible matrices over a specified field K, with the operation of matrix multiplication. A linear group is a group that is isomorphic to a matrix group.
In physics, a charge is any of many different quantities, such as the electric charge in electromagnetism or the color charge in quantum chromodynamics. Charges correspond to the time-invariant generators of a symmetry group, and specifically, to the generators that commute with the Hamiltonian. Charges are often denoted by the letter Q, and so the invariance of the charge corresponds to the vanishing commutator , where H is the Hamiltonian. Thus, charges are associated with conserved quantum numbers; these are the eigenvalues q of the generator Q.
References
- ↑ Burgess, Cliff; Moore, Guy (2006-12-07), The Standard Model: A Primer, Cambridge University Press, p. 492, ISBN 9781139460460 .