In mathematics, and more specifically in abstract algebra, an algebraic structure on a set A is a collection of finitary operations on A; the set A with this structure is also called an algebra.
In mathematics, coalgebras or cogebras are structures that are dual to unital associative algebras. The axioms of unital associative algebras can be formulated in terms of commutative diagrams. Turning all arrows around, one obtains the axioms of coalgebras. Every coalgebra, by duality, gives rise to an algebra, but not in general the other way. In finite dimensions, this duality goes in both directions.
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property. The representation theory of a Hopf algebra is particularly nice, since the existence of compatible comultiplication, counit, and antipode allows for the construction of tensor products of representations, trivial representations, and dual representations.
In category theory, a branch of mathematics, a monad is an endofunctor, together with two natural transformations. Monads are used in the theory of pairs of adjoint functors, and they generalize closure operators on partially ordered sets to arbitrary categories.
Glasgow Haskell Compiler, less commonly known as The Glorious Glasgow Haskell Compilation System or simply GHC, is an open-source native code compiler for the functional programming language Haskell. It provides a cross-platform environment for the writing and testing of Haskell code and it supports numerous extensions, libraries, and optimisations that streamline the process of generating and executing code. GHC is the most commonly-used Haskell compiler. The lead developers are Simon Peyton Jones and Simon Marlow.
In computer science, corecursion is a type of operation that is dual to recursion. Whereas recursion works analytically, starting on data further from a base case and breaking it down into smaller data and repeating until one reaches a base case, corecursion works synthetically, starting from a base case and building it up, iteratively producing data further removed from a base case. Put simply, corecursive algorithms use the data that they themselves produce, bit by bit, as they become available, and needed, to produce further bits of data. A similar but distinct concept is generative recursion which may lack a definite "direction" inherent in corecursion and recursion.
Charity is an experimental purely functional programming language, developed at the University of Calgary under the supervision of Robin Cockett. Based on ideas by Hagino Tatsuya, it is completely grounded in category theory.
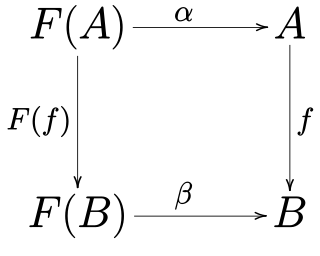
In mathematics, specifically in category theory, an -coalgebra is a structure defined according to a functor . For both algebra and coalgebra, a functor is a convenient and general way of organizing a signature. This has applications in computer science: examples of coalgebras include lazy, infinite data structures, such as streams, and also transition systems.
In universal algebra and mathematical logic, a term algebra is a freely generated algebraic structure over a given signature. For example, in a signature consisting of a single binary operation, the term algebra over a set X of variables is exactly the free magma generated by X. Other synonyms for the notion include absolutely free algebra and anarchic algebra.
In mathematics, an initial algebra is an initial object in the category of -algebras for a given endofunctor . This initiality provides a general framework for induction and recursion.
The Bird–Meertens formalism (BMF) is a calculus for deriving programs from specifications by a process of equational reasoning. It was devised by Richard Bird and Lambert Meertens as part of their work within IFIP Working Group 2.1.
In functional programming, a generalized algebraic data type is a generalization of parametric algebraic data types.
In computer science, coinduction is a technique for defining and proving properties of systems of concurrent interacting objects.
In programming languages and type theory, a product of types is another, compounded, type in a structure. The "operands" of the product are types, and the structure of a product type is determined by the fixed order of the operands in the product. An instance of a product type retains the fixed order, but otherwise may contain all possible instances of its primitive data types. The expression of an instance of a product type will be a tuple, and is called a "tuple type" of expression. A product of types is a direct product of two or more types.
The word anamorph and its derivates may mean: