In mathematics, specifically category theory, a functor is a mapping between categories. Functors were first considered in algebraic topology, where algebraic objects are associated to topological spaces, and maps between these algebraic objects are associated to continuous maps between spaces. Nowadays, functors are used throughout modern mathematics to relate various categories. Thus, functors are important in all areas within mathematics to which category theory is applied.
Standard ML (SML) is a general-purpose, high-level, modular, functional programming language with compile-time type checking and type inference. It is popular for writing compilers, for programming language research, and for developing theorem provers.
In combinatory logic for computer science, a fixed-point combinator, is a higher-order function that returns some fixed point of its argument function, if one exists.
In functional programming, a monad is a structure that combines program fragments (functions) and wraps their return values in a type with additional computation. In addition to defining a wrapping monadic type, monads define two operators: one to wrap a value in the monad type, and another to compose together functions that output values of the monad type. General-purpose languages use monads to reduce boilerplate code needed for common operations. Functional languages use monads to turn complicated sequences of functions into succinct pipelines that abstract away control flow, and side-effects.
In computer science, corecursion is a type of operation that is dual to recursion. Whereas recursion works analytically, starting on data further from a base case and breaking it down into smaller data and repeating until one reaches a base case, corecursion works synthetically, starting from a base case and building it up, iteratively producing data further removed from a base case. Put simply, corecursive algorithms use the data that they themselves produce, bit by bit, as they become available, and needed, to produce further bits of data. A similar but distinct concept is generative recursion, which may lack a definite "direction" inherent in corecursion and recursion.
In mathematics, specifically in category theory, an -coalgebra is a structure defined according to a functor , with specific properties as defined below. For both algebras and coalgebras, a functor is a convenient and general way of organizing a signature. This has applications in computer science: examples of coalgebras include lazy evaluation, infinite data structures, such as streams, and also transition systems.
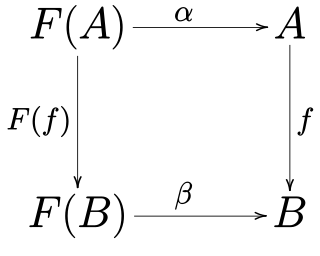
In mathematics, specifically in category theory, F-algebras generalize the notion of algebraic structure. Rewriting the algebraic laws in terms of morphisms eliminates all references to quantified elements from the axioms, and these algebraic laws may then be glued together in terms of a single functor F, the signature.

In computer science, recursion is a method of solving a computational problem where the solution depends on solutions to smaller instances of the same problem. Recursion solves such recursive problems by using functions that call themselves from within their own code. The approach can be applied to many types of problems, and recursion is one of the central ideas of computer science.
The power of recursion evidently lies in the possibility of defining an infinite set of objects by a finite statement. In the same manner, an infinite number of computations can be described by a finite recursive program, even if this program contains no explicit repetitions.
In mathematics, an initial algebra is an initial object in the category of F-algebras for a given endofunctor F. This initiality provides a general framework for induction and recursion.
In functional programming, the concept of catamorphism denotes the unique homomorphism from an initial algebra into some other algebra.
In many programming languages, map is a higher-order function that applies a given function to each element of a collection, e.g. a list or set, returning the results in a collection of the same type. It is often called apply-to-all when considered in functional form.
In functional programming, fold refers to a family of higher-order functions that analyze a recursive data structure and through use of a given combining operation, recombine the results of recursively processing its constituent parts, building up a return value. Typically, a fold is presented with a combining function, a top node of a data structure, and possibly some default values to be used under certain conditions. The fold then proceeds to combine elements of the data structure's hierarchy, using the function in a systematic way.
In computer science, coinduction is a technique for defining and proving properties of systems of concurrent interacting objects.
In computer science, and in particular functional programming, a hylomorphism is a recursive function, corresponding to the composition of an anamorphism followed by a catamorphism. Fusion of these two recursive computations into a single recursive pattern then avoids building the intermediate data structure. This is an example of deforestation, a program optimization strategy. A related type of function is a metamorphism, which is a catamorphism followed by an anamorphism.
In formal methods of computer science, a paramorphism (from Greek παρά, meaning "close together") is an extension of the concept of catamorphism first introduced by Lambert Meertens to deal with a form which “eats its argument and keeps it too”, as exemplified by the factorial function. Its categorical dual is the apomorphism.
In type theory, a system has inductive types if it has facilities for creating a new type from constants and functions that create terms of that type. The feature serves a role similar to data structures in a programming language and allows a type theory to add concepts like numbers, relations, and trees. As the name suggests, inductive types can be self-referential, but usually only in a way that permits structural recursion.
This article describes the features in the programming language Haskell.
In functional programming, an applicative functor, or an applicative for short, is an intermediate structure between functors and monads. In Category Theory they are called Closed Monoidal Functors. Applicative functors allow for functorial computations to be sequenced, but don't allow using results from prior computations in the definition of subsequent ones. Applicative functors are the programming equivalent of lax monoidal functors with tensorial strength in category theory.
In type theory, a polynomial functor is a kind of endofunctor of a category of types that is intimately related to the concept of inductive and coinductive types. Specifically, all W-types are initial algebras of such functors.

In functional programming, a functor is a design pattern inspired by the definition from category theory that allows one to apply a function to values inside a generic type without changing the structure of the generic type. In Haskell this idea can be captured in a type class:





