In celestial mechanics, the argument of latitude () is an angular parameter that defines the position of a body moving along a Kepler orbit. It is the angle between the ascending node and the body.
It is the sum of the more commonly used true anomaly and argument of periapsis.
where is the argument of latitude, the true anomaly, and the argument of periapsis.
Orbital elements are the parameters required to uniquely identify a specific orbit. In celestial mechanics these elements are considered in two-body systems using a Kepler orbit. There are many different ways to mathematically describe the same orbit, but certain schemes, each consisting of a set of six parameters, are commonly used in astronomy and orbital mechanics.
In thermodynamics and solid-state physics, the Debye model is a method developed by Peter Debye in 1912 to estimate phonon contribution to the specific heat in a solid. It treats the vibrations of the atomic lattice (heat) as phonons in a box in contrast to the Einstein photoelectron model, which treats the solid as many individual, non-interacting quantum harmonic oscillators. The Debye model correctly predicts the low-temperature dependence of the heat capacity of solids, which is proportional to – the Debye T 3 law. Similarly to the Einstein photoelectron model, it recovers the Dulong–Petit law at high temperatures. Due to simplifying assumptions, its accuracy suffers at intermediate temperatures.
The Ekman number (Ek) is a dimensionless number used in fluid dynamics to describe the ratio of viscous forces to Coriolis forces. It is frequently used in describing geophysical phenomena in the oceans and atmosphere in order to characterise the ratio of viscous forces to the Coriolis forces arising from planetary rotation. It is named after the Swedish oceanographer Vagn Walfrid Ekman.
In celestial mechanics, true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse.
The argument of periapsis, symbolized as ω (omega), is one of the orbital elements of an orbiting body. Parametrically, ω is the angle from the body's ascending node to its periapsis, measured in the direction of motion.
In celestial mechanics, the longitude of the periapsis, also called longitude of the pericenter, of an orbiting body is the longitude at which the periapsis would occur if the body's orbit inclination were zero. It is usually denoted ϖ.
In celestial mechanics, true longitude is the ecliptic longitude at which an orbiting body could actually be found if its inclination were zero. Together with the inclination and the ascending node, the true longitude can tell us the precise direction from the central object at which the body would be located at a particular time.
In astrodynamics or celestial mechanics a parabolic trajectory is a Kepler orbit with the eccentricity equal to 1 and is an unbound orbit that is exactly on the border between elliptical and hyperbolic. When moving away from the source it is called an escape orbit, otherwise a capture orbit. It is also sometimes referred to as a C3 = 0 orbit (see Characteristic energy).
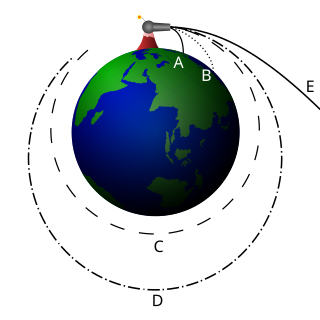
A circular orbit is an orbit with a fixed distance around the barycenter; that is, in the shape of a circle. In this case, not only the distance, but also the speed, angular speed, potential and kinetic energy are constant. There is no periapsis or apoapsis. This orbit has no radial version.
Spacecraft flight dynamics is the application of mechanical dynamics to model how the external forces acting on a space vehicle or spacecraft determine its flight path. These forces are primarily of three types: propulsive force provided by the vehicle's engines; gravitational force exerted by the Earth and other celestial bodies; and aerodynamic lift and drag.
In atomic, molecular, and optical physics, the Einstein coefficients are quantities describing the probability of absorption or emission of a photon by an atom or molecule. The Einstein A coefficients are related to the rate of spontaneous emission of light, and the Einstein B coefficients are related to the absorption and stimulated emission of light. Throughout this article, "light" refers to any electromagnetic radiation, not necessarily in the visible spectrum.
In differential geometry and mathematical physics, a spin connection is a connection on a spinor bundle. It is induced, in a canonical manner, from the affine connection. It can also be regarded as the gauge field generated by local Lorentz transformations. In some canonical formulations of general relativity, a spin connection is defined on spatial slices and can also be regarded as the gauge field generated by local rotations.
The perifocal coordinate (PQW) system is a frame of reference for an orbit. The frame is centered at the focus of the orbit, i.e. the celestial body about which the orbit is centered. The unit vectors and lie in the plane of the orbit. is directed towards the periapsis of the orbit and has a true anomaly of 90 degrees past the periapsis. The third unit vector is the angular momentum vector and is directed orthogonal to the orbital plane such that:
Orbit determination is the estimation of orbits of objects such as moons, planets, and spacecraft. One major application is to allow tracking newly observed asteroids and verify that they have not been previously discovered. The basic methods were discovered in the 17th century and have been continuously refined.
In general relativity, Lense–Thirring precession or the Lense–Thirring effect is a relativistic correction to the precession of a gyroscope near a large rotating mass such as the Earth. It is a gravitomagnetic frame-dragging effect. It is a prediction of general relativity consisting of secular precessions of the longitude of the ascending node and the argument of pericenter of a test particle freely orbiting a central spinning mass endowed with angular momentum .
In celestial mechanics, a Kepler orbit is the motion of one body relative to another, as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space. A Kepler orbit can also form a straight line. It considers only the point-like gravitational attraction of two bodies, neglecting perturbations due to gravitational interactions with other objects, atmospheric drag, solar radiation pressure, a non-spherical central body, and so on. It is thus said to be a solution of a special case of the two-body problem, known as the Kepler problem. As a theory in classical mechanics, it also does not take into account the effects of general relativity. Keplerian orbits can be parametrized into six orbital elements in various ways.
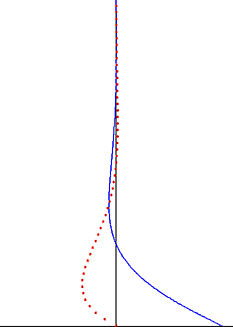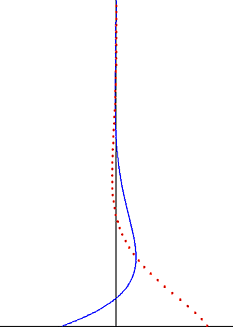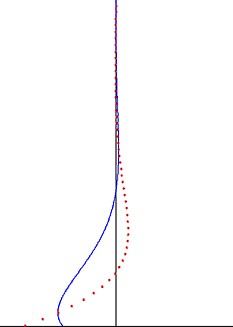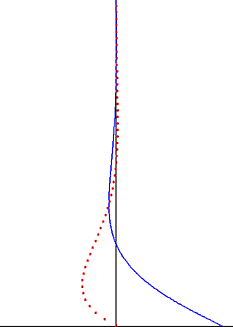
In fluid dynamics, Stokes problem also known as Stokes second problem or sometimes referred to as Stokes boundary layer or Oscillating boundary layer is a problem of determining the flow created by an oscillating solid surface, named after Sir George Stokes. This is considered one of the simplest unsteady problems that has an exact solution for the Navier–Stokes equations. In turbulent flow, this is still named a Stokes boundary layer, but now one has to rely on experiments, numerical simulations or approximate methods in order to obtain useful information on the flow.
Buchholz's psi-functions are a hierarchy of single-argument ordinal functions introduced by German mathematician Wilfried Buchholz in 1986. These functions are a simplified version of the -functions, but nevertheless have the same strength as those. Later on this approach was extended by Jäger and Schütte.
In set theory and logic, Buchholz's ID hierarchy is a hierarchy of subsystems of first-order arithmetic. The systems/theories are referred to as "the formal theories of ν-times iterated inductive definitions". IDν extends PA by ν iterated least fixed points of monotone operators.
In theoretical physics, more specifically in quantum field theory and supersymmetry, supersymmetric Yang–Mills, also known as super Yang–Mills and abbreviated to SYM, is a supersymmetric generalization of Yang–Mills theory, which is a gauge theory that plays an important part in the mathematical formulation of forces in particle physics. It is a special case of 4D N = 1 global supersymmetry.
 | This astronomy-related article is a stub. You can help Wikipedia by expanding it. |
