
Ashok Malhotra (born 1950, Pune, India) is an Indian professor, higher education professional and author.

Ashok Malhotra (born 1950, Pune, India) is an Indian professor, higher education professional and author.
Ashok Malhotra is the son of Colonel A. P. Malhotra and Nand Rani Malhotra (Nando). He is the brother of Lt. General Anoop Malhotra. He graduated from the Indian Institute of Technology at Delhi in 1971 with a degree in Mechanical Engineering, and received a doctoral degree in Mechanical Engineering from the University of British Columbia, Canada in 1978. [1]
Malhotra began his academic career as a lecturer at IIT Delhi in 1978, where, although he earned much respect of colleagues, he earned flak of establishment for his bold and independent stance on work and academic policy. To quote from a report in a 1981 issue of 'India Today' a prominent news magazine,
Jain (The Director) dismisses this frustration as "rumour mongering" and says that staffers should submit their grievances to him and not to the press. He dismisses the fear of victimisation but forgets that late last year Ashok Malhotra, a lecturer who is immensely respected by his colleagues and was at the Centre of Energy Studies, was abruptly served with a termination notice. But was later reinstated in the Mechanical Engineering Department. [2]
Malhotra has been on the faculty of the Indian Institute of Technology, Delhi, The University of British Columbia Canada and the University of Mosul in Iraq. His most recent appointment during 2009–2010 was as the Director of the Amrapali Institute of Technology and Sciences, AITS in the Nainital District of India.
Malhotra has had special interests in supercritical fluids. His Ph.D. Thesis was on supercritical carbon dioxide. He has also worked on the optimal design of power plants using supercritical steam and written a book on supercritical steam. Following is a quotation on it by Christopher Mims,
Supercritical steam has already been used in coal-fired and nuclear power plants. The mechanism by which it yields higher efficiency is complicated, but ultimately it boils down to this: steam turbines need very hot steam in order to produce power, and supercritical steam is much closer to this temperature than cooler steam, says Ashok Malhotra, who literally wrote the book on the subject (Thermodynamic Properties of Supercritical Steam). [3]
The Turbulent Prandtl number is a non-dimensional parameter required in convective turbulent heat transfer calculations. The simplest model for turbulent Prandtl Number is the Reynolds analogy, which yields a turbulent Prandtl number of unity. However, from experimental data based on air or water adjustments have been made to values slightly different from unity. Its counterpart the Prandtl number is employed in laminar flow calculations. However, most flows in nature are turbulent rather than laminar and therefore incorporating the use of turbulent Prandtl Number becomes necessary. Its use can be entirely bypassed through more complicated and advanced heat flux modelling but challenges still remain in its formulation. Ashok Malhotra and Kang (1984) [4] showed through calculations in a circular pipe that the Turbulent Prandtl Number is not close to unity but rather a strong function of the molecular Prandtl number amongst other parameters . They developed relationships between the turbulent and molecular Prandtl number that can be employed in convective heat transfer calculations. Their work has been substantiated by other researchers e.g.. McEligot and Taylor, 1996 [5] and Churchill [6]
Recent publications by Malhotra include, How to Create excellent Universities [7] and Steam Property Tables [8] Some publications from his research areas of solar energy, heat transfer and fluid flow are, Minimizing convective heat losses in flat plate solar collectors, [9] Modelling the flow in a Hydrocyclone, [10] Optimal Geometries of Solar concentrators., [11] heat exchangers [12] and thermodynamic properties of steam [13]
Aside from his professional interests in higher education, science and technology, Malhotra's interest range from the environment to the economy; from ancient history to philosophy. He regularly shares his views on such topics with the wider online community through his blogs. He has also authored a novel and a novella that elaborate his environmental and philosophical views through the medium of fiction.
In thermal fluid dynamics, the Nusselt number is the ratio of convective to conductive heat transfer at a boundary in a fluid. Convection includes both advection and diffusion (conduction). The conductive component is measured under the same conditions as the convective but for a hypothetically motionless fluid. It is a dimensionless number, closely related to the fluid's Rayleigh number.

Heat transfer is a discipline of thermal engineering that concerns the generation, use, conversion, and exchange of thermal energy (heat) between physical systems. Heat transfer is classified into various mechanisms, such as thermal conduction, thermal convection, thermal radiation, and transfer of energy by phase changes. Engineers also consider the transfer of mass of differing chemical species, either cold or hot, to achieve heat transfer. While these mechanisms have distinct characteristics, they often occur simultaneously in the same system.
In fluid dynamics, the Darcy–Weisbach equation is an empirical equation that relates the head loss, or pressure loss, due to friction along a given length of pipe to the average velocity of the fluid flow for an incompressible fluid. The equation is named after Henry Darcy and Julius Weisbach. Currently, there is no formula more accurate or universally applicable than the Darcy-Weisbach supplemented by the Moody diagram or Colebrook equation.

In physics and fluid mechanics, a boundary layer is the thin layer of fluid in the immediate vicinity of a bounding surface formed by the fluid flowing along the surface. The fluid's interaction with the wall induces a no-slip boundary condition. The flow velocity then monotonically increases above the surface until it returns to the bulk flow velocity. The thin layer consisting of fluid whose velocity has not yet returned to the bulk flow velocity is called the velocity boundary layer.

The Rankine cycle is an idealized thermodynamic cycle describing the process by which certain heat engines, such as steam turbines or reciprocating steam engines, allow mechanical work to be extracted from a fluid as it moves between a heat source and heat sink. The Rankine cycle is named after William John Macquorn Rankine, a Scottish polymath professor at Glasgow University.
A supercritical fluid (SCF) is any substance at a temperature and pressure above its critical point, where distinct liquid and gas phases do not exist, but below the pressure required to compress it into a solid. It can effuse through porous solids like a gas, overcoming the mass transfer limitations that slow liquid transport through such materials. SCF are much superior to gases in their ability to dissolve materials like liquids or solids. Also, near the critical point, small changes in pressure or temperature result in large changes in density, allowing many properties of a supercritical fluid to be "fine-tuned".
Thermofluids is a branch of science and engineering encompassing four intersecting fields:
In thermodynamics, the heat transfer coefficient or film coefficient, or film effectiveness, is the proportionality constant between the heat flux and the thermodynamic driving force for the flow of heat. It is used in calculating the heat transfer, typically by convection or phase transition between a fluid and a solid. The heat transfer coefficient has SI units in watts per square meter per kelvin (W/m2/K).
Thermal hydraulics is the study of hydraulic flow in thermal fluids. The area can be mainly divided into three parts: thermodynamics, fluid mechanics, and heat transfer, but they are often closely linked to each other. A common example is steam generation in power plants and the associated energy transfer to mechanical motion and the change of states of the water while undergoing this process. Thermal-hydraulic analysis can determine important parameters for reactor design such as plant efficiency and coolability of the system.
In fluid dynamics, the Schmidt number of a fluid is a dimensionless number defined as the ratio of momentum diffusivity and mass diffusivity, and it is used to characterize fluid flows in which there are simultaneous momentum and mass diffusion convection processes. It was named after German engineer Ernst Heinrich Wilhelm Schmidt (1892–1975).

The steam-electric power station is a power station in which the electric generator is steam driven. Water is heated, turns into steam and spins a steam turbine which drives an electrical generator. After it passes through the turbine, the steam is condensed in a condenser. The greatest variation in the design of steam-electric power plants is due to the different fuel sources.

In fluid dynamics, drag crisis is a phenomenon in which drag coefficient drops off suddenly as Reynolds number increases. This has been well studied for round bodies like spheres and cylinders. The drag coefficient of a sphere will change rapidly from about 0.5 to 0.2 at a Reynolds number in the range of 300000. This corresponds to the point where the flow pattern changes, leaving a narrower turbulent wake. The behavior is highly dependent on small differences in the condition of the surface of the sphere.
The Reynolds Analogy is popularly known to relate turbulent momentum and heat transfer. That is because in a turbulent flow the transport of momentum and the transport of heat largely depends on the same turbulent eddies: the velocity and the temperature profiles have the same shape.
The turbulent Prandtl number (Prt) is a non-dimensional term defined as the ratio between the momentum eddy diffusivity and the heat transfer eddy diffusivity. It is useful for solving the heat transfer problem of turbulent boundary layer flows. The simplest model for Prt is the Reynolds analogy, which yields a turbulent Prandtl number of 1. From experimental data, Prt has an average value of 0.85, but ranges from 0.7 to 0.9 depending on the Prandtl number of the fluid in question.
Concentric Tube Heat Exchangers are used in a variety of industries for purposes such as material processing, food preparation, and air-conditioning. They create a temperature driving force by passing fluid streams of different temperatures parallel to each other, separated by a physical boundary in the form of a pipe. This induces forced convection, transferring heat to/from the product.
In engineering, physics, and chemistry, the study of transport phenomena concerns the exchange of mass, energy, charge, momentum and angular momentum between observed and studied systems. While it draws from fields as diverse as continuum mechanics and thermodynamics, it places a heavy emphasis on the commonalities between the topics covered. Mass, momentum, and heat transport all share a very similar mathematical framework, and the parallels between them are exploited in the study of transport phenomena to draw deep mathematical connections that often provide very useful tools in the analysis of one field that are directly derived from the others.
In fluid dynamics, the entrance length is the distance a flow travels after entering a pipe before the flow becomes fully developed. Entrance length refers to the length of the entry region, the area following the pipe entrance where effects originating from the interior wall of the pipe propagate into the flow as an expanding boundary layer. When the boundary layer expands to fill the entire pipe, the developing flow becomes a fully developed flow, where flow characteristics no longer change with increased distance along the pipe. Many different entrance lengths exist to describe a variety of flow conditions. Hydrodynamic entrance length describes the formation of a velocity profile caused by viscous forces propagating from the pipe wall. Thermal entrance length describes the formation of a temperature profile. Awareness of entrance length may be necessary for the effective placement of instrumentation, such as fluid flow meters.
The removal of heat from nuclear reactors is an essential step in the generation of energy from nuclear reactions. In nuclear engineering there are a number of empirical or semi-empirical relations used for quantifying the process of removing heat from a nuclear reactor core so that the reactor operates in the projected temperature interval that depends on the materials used in the construction of the reactor. The effectiveness of removal of heat from the reactor core depends on many factors, including the cooling agents used and the type of reactor. Common liquid coolants for nuclear reactors include: deionized water, heavy water, the lighter alkaline metals, lead or lead-based eutectic alloys like lead-bismuth, and NaK, a eutectic alloy of sodium and potassium. Gas cooled reactors operate with coolants like carbon dioxide, helium or nitrogen but some very low powered research reactors have even been air-cooled with Chicago Pile 1 relying on natural convection of the surrounding air to remove the negligible thermal power output. There is ongoing research into using supercritical fluids as reactor coolants but thus far neither the supercritical water reactor nor a reactor cooled with supercritical Carbon Dioxide nor any other kind of supercritical-fluid-cooled reactor has ever been built.
David S-K Ting is a Canadian academic, author and researcher. He is a professor of mechanical, automotive & materials engineering at the University of Windsor. He is the founder of the Turbulence & Energy Laboratory.
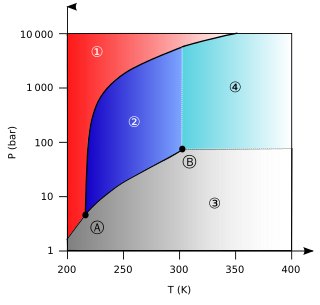
Supercritical carbon dioxide blend (sCO2 blend) is an homogeneous mixture of CO2 with one or more fluids (dopant fluid) where it is held at or above its critical temperature and critical pressure.