Related Research Articles
In mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the x or y coordinates tends to infinity. In projective geometry and related contexts, an asymptote of a curve is a line which is tangent to the curve at a point at infinity.
A sphere is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. Formally, a sphere is the set of points that are all at the same distance r from a given point in three-dimensional space. That given point is the center of the sphere, and r is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians.
In mathematics, curvature is any of several strongly related concepts in geometry that intuitively measure the amount by which a curve deviates from being a straight line or by which a surface deviates from being a plane. If a curve or surface is contained in a larger space, curvature can be defined extrinsically relative to the ambient space. Curvature of Riemannian manifolds of dimension at least two can be defined intrinsically without reference to a larger space.
In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principal axes. A hyperboloid is the surface obtained from a hyperboloid of revolution by deforming it by means of directional scalings, or more generally, of an affine transformation.
In mathematics, hyperbolic geometry is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
Gauss's Theorema Egregium is a major result of differential geometry, proved by Carl Friedrich Gauss in 1827, that concerns the curvature of surfaces. The theorem says that Gaussian curvature can be determined entirely by measuring angles, distances and their rates on a surface, without reference to the particular manner in which the surface is embedded in the ambient 3-dimensional Euclidean space. In other words, the Gaussian curvature of a surface does not change if one bends the surface without stretching it. Thus the Gaussian curvature is an intrinsic invariant of a surface.
In differential geometry, the Gaussian curvature or Gauss curvatureΚ of a smooth surface in three-dimensional space at a point is the product of the principal curvatures, κ1 and κ2, at the given point: The Gaussian radius of curvature is the reciprocal of Κ. For example, a sphere of radius r has Gaussian curvature 1/r2 everywhere, and a flat plane and a cylinder have Gaussian curvature zero everywhere. The Gaussian curvature can also be negative, as in the case of a hyperboloid or the inside of a torus.
In differential geometry, the Gauss map of a surface is a function that maps each point in the surface to a unit vector that is orthogonal to the surface at that point. Namely, given a surface X in Euclidean space R3, the Gauss map is a map N: X → S2 (where S2 is the unit sphere) such that for each p in X, the function value N(p) is a unit vector orthogonal to X at p. The Gauss map is named after Carl F. Gauss.
In differential geometry, the two principal curvatures at a given point of a surface are the maximum and minimum values of the curvature as expressed by the eigenvalues of the shape operator at that point. They measure how the surface bends by different amounts in different directions at that point.
In mathematics, a surface is a mathematical model of the common concept of a surface. It is a generalization of a plane, but, unlike a plane, it may be curved; this is analogous to a curve generalizing a straight line.
In the differential geometry of surfaces in three dimensions, umbilics or umbilical points are points on a surface that are locally spherical. At such points the normal curvatures in all directions are equal, hence, both principal curvatures are equal, and every tangent vector is a principal direction. The name "umbilic" comes from the Latin umbilicus (navel).
In differential geometry, the Dupin indicatrix is a method for characterising the local shape of a surface. Draw a plane parallel to the tangent plane and a small distance away from it. Consider the intersection of the surface with this plane. The shape of the intersection is related to the Gaussian curvature. The Dupin indicatrix is the result of the limiting process as the plane approaches the tangent plane. The indicatrix was introduced by Charles Dupin.
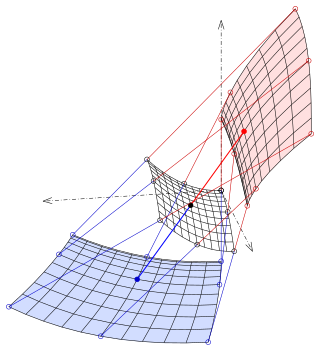
For a surface in three dimension the focal surface, surface of centers or evolute is formed by taking the centers of the curvature spheres, which are the tangential spheres whose radii are the reciprocals of one of the principal curvatures at the point of tangency. Equivalently it is the surface formed by the centers of the circles which osculate the curvature lines.
In the mathematical study of the differential geometry of surfaces, a tangent developable is a particular kind of developable surface obtained from a curve in Euclidean space as the surface swept out by the tangent lines to the curve. Such a surface is also the envelope of the tangent planes to the curve.
In hyperbolic geometry, a horocycle, sometimes called an oricycle or limit circle, is a curve of constant curvature which converges asymptotically in both directions to a single ideal point, called the centre of the horocycle. The perpendicular geodesics through every point on a horocycle are limiting parallels, and also all converge asymptotically to the centre. It is the two-dimensional case of a horosphere.
In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth surfaces with various additional structures, most often, a Riemannian metric. Surfaces have been extensively studied from various perspectives: extrinsically, relating to their embedding in Euclidean space and intrinsically, reflecting their properties determined solely by the distance within the surface as measured along curves on the surface. One of the fundamental concepts investigated is the Gaussian curvature, first studied in depth by Carl Friedrich Gauss, who showed that curvature was an intrinsic property of a surface, independent of its isometric embedding in Euclidean space.
A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though it was sometimes called as a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties.
In geometry, a convex curve is a plane curve that has a supporting line through each of its points. There are many other equivalent definitions of these curves, going back to Archimedes. Examples of convex curves include the convex polygons, the boundaries of convex sets, and the graphs of convex functions. Important subclasses of convex curves include the closed convex curves, the smooth curves that are convex, and the strictly convex curves, which have the additional property that each supporting line passes through a unique point of the curve.
A normal plane is any plane containing the normal vector of a surface at a particular point.
References
- ↑ David Hilbert; Cohn-Vossen, S. (1999). Geometry and Imagination. American Mathematical Society. ISBN 0-8218-1998-4.