
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the x or y coordinates tends to infinity. In projective geometry and related contexts, an asymptote of a curve is a line which is tangent to the curve at a point at infinity.

In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity , a number ranging from to .

In mathematics, an elliptic curve is a smooth, projective, algebraic curve of genus one, on which there is a specified point O. An elliptic curve is defined over a field K and describes points in K2, the Cartesian product of K with itself. If the field's characteristic is different from 2 and 3, then the curve can be described as a plane algebraic curve which consists of solutions (x, y) for:

In mathematics, a hyperbola is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane and a double cone. If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola.

In economics, an indifference curve connects points on a graph representing different quantities of two goods, points between which a consumer is indifferent. That is, any combinations of two products indicated by the curve will provide the consumer with equal levels of utility, and the consumer has no preference for one combination or bundle of goods over a different combination on the same curve. One can also refer to each point on the indifference curve as rendering the same level of utility (satisfaction) for the consumer. In other words, an indifference curve is the locus of various points showing different combinations of two goods providing equal utility to the consumer. Utility is then a device to represent preferences rather than something from which preferences come. The main use of indifference curves is in the representation of potentially observable demand patterns for individual consumers over commodity bundles.
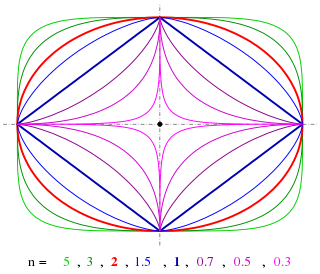
A superellipse, also known as a Lamé curve after Gabriel Lamé, is a closed curve resembling the ellipse, retaining the geometric features of semi-major axis and semi-minor axis, and symmetry about them, but a different overall shape.
In the mathematical field of differential geometry, a metric tensor is an additional structure on a manifold M that allows defining distances and angles, just as the inner product on a Euclidean space allows defining distances and angles there. More precisely, a metric tensor at a point p of M is a bilinear form defined on the tangent space at p, and a metric field on M consists of a metric tensor at each point p of M that varies smoothly with p.
In vector calculus, Green's theorem relates a line integral around a simple closed curve C to a double integral over the plane region D bounded by C. It is the two-dimensional special case of Stokes' theorem.

In geometry, a solid of revolution is a solid figure obtained by rotating a plane figure around some straight line, which may not intersect the generatrix. The surface created by this revolution and which bounds the solid is the surface of revolution.

A surface of revolution is a surface in Euclidean space created by rotating a curve one full revolution around an axis of rotation . The volume bounded by the surface created by this revolution is the solid of revolution.
In mathematics, particularly differential geometry, a Finsler manifold is a differentiable manifold M where a (possibly asymmetric) Minkowski normF(x, −) is provided on each tangent space TxM, that enables one to define the length of any smooth curve γ : [a, b] → M as

In mathematics, a parametric equation defines a group of quantities as functions of one or more independent variables called parameters. Parametric equations are commonly used to express the coordinates of the points that make up a geometric object such as a curve or surface, called a parametric curve and parametric surface, respectively. In such cases, the equations are collectively called a parametric representation, or parametric system, or parameterization of the object.
In the mathematical field of complex analysis, contour integration is a method of evaluating certain integrals along paths in the complex plane.

An osculating circle is a circle that best approximates the curvature of a curve at a specific point. It is tangent to the curve at that point and has the same curvature as the curve at that point. The osculating circle provides a way to understand the local behavior of a curve and is commonly used in differential geometry and calculus.

Arc length is the distance between two points along a section of a curve.

In differential geometry, the torsion tensor is a tensor that is associated to any affine connection. The torsion tensor is bilinear map of two input vectors , that produces an output vector representing the displacement within a tangent space when the tangent space is developed along an infinitesimal parallelogram whose sides are . It is skew symmetric in its inputs, because developing over the parallelogram in the opposite sense produces the opposite displacement, similarly to how a screw moves in opposite ways when it is twisted in two directions.
Special affine curvature, also known as the equiaffine curvature or affine curvature, is a particular type of curvature that is defined on a plane curve that remains unchanged under a special affine transformation. The curves of constant equiaffine curvature k are precisely all non-singular plane conics. Those with k > 0 are ellipses, those with k = 0 are parabolae, and those with k < 0 are hyperbolae.
The gradient theorem, also known as the fundamental theorem of calculus for line integrals, says that a line integral through a gradient field can be evaluated by evaluating the original scalar field at the endpoints of the curve. The theorem is a generalization of the second fundamental theorem of calculus to any curve in a plane or space rather than just the real line.

In inversive geometry, an inverse curve of a given curve C is the result of applying an inverse operation to C. Specifically, with respect to a fixed circle with center O and radius k the inverse of a point Q is the point P for which P lies on the ray OQ and OP·OQ = k2. The inverse of the curve C is then the locus of P as Q runs over C. The point O in this construction is called the center of inversion, the circle the circle of inversion, and k the radius of inversion.
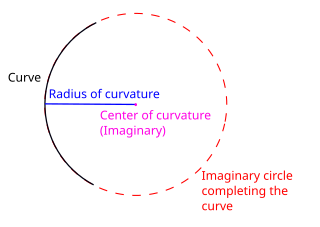
In differential geometry, the radius of curvature, R, is the reciprocal of the curvature. For a curve, it equals the radius of the circular arc which best approximates the curve at that point. For surfaces, the radius of curvature is the radius of a circle that best fits a normal section or combinations thereof.















