Axiomatic theory of receptive fields

Scale space
	Scale-space axioms
	Scale-space implementation
Feature detection
	Edge detection
	Blob detection
	Corner detection
	Ridge detection
	Interest point detection
Scale selection
Affine shape adaptation
Scale-space segmentation
Axiomatic theory of receptive fields
	v ; t ; e ;

Last updated November 14, 2019

Receptive field profiles registered by cell recordings have shown that mammalian vision has developed receptive fields tuned to different sizes and orientations in the image domain as well as to different image velocities in space-time.^[1]^[2]^[3]^[4]^[5] Corresponding cell recordings in the auditory system has shown that mammals have developed receptive fields tuned to different frequencies as well as temporal transients.^[6]^[7]^[8]^[9] This article describes normative theories that have been developed to explain these properties of sensory receptive fields based on structural properties of the environment. Beyond theoretical explanation of biological phenomena, these theories can also be used for computational modelling of biological receptive fields and for building algorithms for artificial perception based on sensory data.

Computational theory of visual receptive fields

Idealized models of visual receptive fields similar to those found in the retina, the lateral geniculate nucleus and the primary visual cortex of higher mammals can be derived in an axiomatic way from structural requirements on the first stages of visual processing that reflect symmetry properties of the surrounding world in combination with additional assumptions to ensure internally consistent image representations at multiple spatial and temporal scales.^[10]^[11] Specifically, idealized functional models for linear spatio-temporal receptive fields can be derived in a principled manner to constitute a combination of Gaussian derivatives over the spatial domain and either non-causal Gaussian derivatives or truly time-causal temporal scale-space kernels over the temporal domain: ^[10]^[11]^[12]

T(x_{1},x_{2},t;\;s,\tau ;\;v,\Sigma )=\partial _{\varphi }^{m_{1}}\partial _{\bot \varphi }^{m_{2}}\partial _{\bar {t}}^{n}\left(g(x_{1}-v_{1}t,x_{2}-v_{2}t;\;s,\Sigma )\,h(t;\;\tau )\right)

where

$x=(x_{1},x_{2})^{T}$ denotes the image coordinates,
$t$ denotes time,
$s$ denotes the spatial scale,
$\tau$ denotes the temporal scale,
$v=(v_{1},v_{2})^{T}$ denotes a local image velocity,
$\Sigma$ denotes a spatial covariance matrix determining the spatial shape of an affine Gaussian kernel,
$m_{1}$ and $m_{2}$ denotes orders of spatial differentiation,
$n$ denotes the order of temporal differentiation,
$\partial _{\varphi }=\cos \varphi \,\partial _{x_{1}}+\sin \varphi \,\partial _{x_{2}}$ and $\partial _{\bot \varphi }=\sin \varphi \,\partial _{x_{1}}-\cos \varphi \,\partial _{x_{2}}$ denote spatial directional derivative operators in two orthogonal directions $\varphi$ and $\bot \varphi$ ,
$g(x;\;s,\Sigma )={\frac {1}{2\pi s{\sqrt {\det \Sigma }}}}e^{-x^{T}\Sigma ^{-1}x/2s}$ is an affine Gaussian kernel with its size determined by the spatial scale parameter $s$ and its shape by the spatial covariance matrix $\Sigma$ ,
$g(x_{1}-v_{1}t,x_{2}-v_{2}t;\;s,\Sigma )$ denotes a spatial affine Gaussian kernel that moves with image velocity $v=(v_{1},v_{2})$ in space-time and
$h(t;\;\tau )$ is a temporal smoothing kernel over time corresponding to a Gaussian kernel in the case of non-causal time or a cascade of first-order integrators or equivalently truncated exponential kernels coupled in cascade over a time-causal temporal domain.

Correspondingly, and with similar notation idealized functional models for spatial receptive fields can be expressed of the form

T(x_{1},x_{2};\;s,\Sigma )=\partial _{\varphi }^{m_{1}}\partial _{\bot \varphi }^{m_{2}}\left(g(x_{1},x_{2};\;s,\Sigma )\right).

This model specifically generalizes the receptive field model in terms of Gaussian derivatives^[13]^[14]^[15]^[16]^[17]

T(x_{1},x_{2};\;s)=\partial _{\varphi }^{m_{1}}\partial _{\bot \varphi }^{m_{2}}\left(g(x_{1},x_{2};\;s)\right)

from directional derivatives of rotationally Gaussian kernels $g(x_{1},x_{2};\;s)$ to directional derivatives of affine Gaussian kernels $g(x_{1},x_{2};\;s,\Sigma )$ .

Idealized functional models of receptive fields of these forms have been shown to quite well reproduce the shape of spatial and spatio-temporal receptive fields measured by cell recordings of neurons in the LGN and of simple cells in the primary visual cortex (V1).^[10]^[11]^[12]^[3]^[4]

Theoretical arguments have been presented of preferring this generalized Gaussian model of receptive fields over a Gabor model of receptive fields, because of the better theoretical properties of the generalized Gaussian model under natural image transformations.^[10]^[18] Specifically, these generalized Gaussian receptive fields can be shown to enable computation of invariant visual representations under natural image transformations.^[18] By these results, the different shapes of receptive field profiles found in biological vision, which are tuned to different sizes and orientations in the image domain as well as to different image velocities in space-time, can be seen as well adapted to structure of the physical world and be explained from the requirement that the visual system should have the possibility of being invariant to the natural types of image transformations that occur in its environment.^[10]^[11]^[18]

Computational theory of auditory receptive fields

A computational theory for auditory receptive fields can be expressed in a structurally similar way, permitting the derivation of auditory receptive fields in two stages:^[19]^[20]

a first stage of temporal receptive fields corresponding to an idealized cochlea model modeled as a windowed Fourier transform

S(t,\omega ;\;\tau )=\int _{t'=-\infty }^{\infty }f(t')\,e^{-i\omega t'}\,w(t-t';\;\tau )\,dt'

where $t$ denotes time, $\omega$ denotes the angular frequency, $\tau$ denotes the temporal scale of the window function $w$ , which can be chosen as either Gabor functions in the case of non-causal time or Gammatone functions alternatively generalized Gammatone functions for a truly time-causal model in which the future cannot be accessed,

a second layer of spectra-temporal receptive fields

A_{\alpha ,\beta }(t,\nu ;\;\Sigma )=\partial _{t}^{\alpha }\partial _{\nu }^{\beta }\left(g(\nu -vt;\;s)\,T(t;\;\tau )\right)

applied to the magnitude of the logarithmically transformed spectrogram

S_{dB}=20\log _{10}\left({\frac {|S|}{S_{0}}}\right)

where

$\nu$ denotes the logarithmic frequency,
$\Sigma$ is a spectro-temporal covariance matrix determining the shape of the second-layer receptive field over the spectro-temporal domain,
$\alpha$ is the order of temporal differentiation,
$\beta$ is the order of logspectral differentiation,
the smoothing over the logspectral domain is modeled as a Gaussian function $g(\nu -vt;\;s)$ extended with glissando adaptation with
a glissando parameter $v$ to account for frequency variations over time

and with the temporal smoothing kernels $T(t;\;\tau )$ chosen as either Gaussian kernels over time in the case of non-causal time or first-order integrators (truncated exponential kernels) coupled in cascade in the case of truly time-causal operations.

The shapes of the receptive field functions in these models can be determined by necessity from structural properties of the environment combined with requirements about the internal structure of the auditory system to enable theoretically well-founded processing of sound signals at different temporal and log-spectral scales. Specifically, the resulting spectro-temporal fields in this model obey invariance or covariance properties over natural sound transformations including: (i) temporal shifts, (ii) variations in sound pressure, (iii) the distance between the sound source and the observer, (iv) a shift in the frequencies of auditory stimuli and (v) glissando transformations.^[19]^[20]

Idealized receptive fields of this form can be shown to well model the qualitative shape of spectro-temporal receptive fields as measured by cell recordings in the inferior colliculus (ICC) as well as the linear component of some receptive fields measured in the primary auditory cortex.^[19]^[20]

External links

Alonso, J.-M., & Chen, Y. (2008). Receptive field. Scholarpedia, 4(1), 5393. doi: 10.4249/scholarpedia.5393

Related Research Articles

In probability theory, the normaldistribution is a very common continuous probability distribution. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. A random variable with a Gaussian distribution is said to be normally distributed and is called a normal deviate.

Noether's theorem states that every differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proven by mathematician Emmy Noether in 1915 and published in 1918, after a special case was proven by E. Cosserat and F. Cosserat in 1909. The action of a physical system is the integral over time of a Lagrangian function, from which the system's behavior can be determined by the principle of least action. This theorem only applies to continuous and smooth symmetries over physical space.

In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in mechanical engineering and theoretical physics. It arises, for instance, to describe the potential field caused by a given charge or mass density distribution; with the potential field known, one can then calculate gravitational or electrostatic field. It is a generalization of Laplace's equation, which is also frequently seen in physics. The equation is named after the French mathematician, geometer, and physicist Siméon Denis Poisson.

In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the form:

Parabolic coordinates are a two-dimensional orthogonal coordinate system in which the coordinate lines are confocal parabolas. A three-dimensional version of parabolic coordinates is obtained by rotating the two-dimensional system about the symmetry axis of the parabolas.

Large eddy simulation (LES) is a mathematical model for turbulence used in computational fluid dynamics. It was initially proposed in 1963 by Joseph Smagorinsky to simulate atmospheric air currents, and first explored by Deardorff (1970). LES is currently applied in a wide variety of engineering applications, including combustion, acoustics, and simulations of the atmospheric boundary layer.

In quantum field theory, a quartic interaction is a type of self-interaction in a scalar field. Other types of quartic interactions may be found under the topic of four-fermion interactions. A classical free scalar field $satisfies the Klein-Gordon equation. If a scalar field is denoted, a quartic interaction is represented by adding a potential term to the Lagrangian density. The coupling constant is dimensionless in 4-dimensional spacetime.$

In statistics, econometrics and signal processing, an autoregressive (AR) model is a representation of a type of random process; as such, it is used to describe certain time-varying processes in nature, economics, etc. The autoregressive model specifies that the output variable depends linearly on its own previous values and on a stochastic term ; thus the model is in the form of a stochastic difference equation. Together with the moving-average (MA) model, it is a special case and key component of the more general ARMA and ARIMA models of time series, which have a more complicated stochastic structure; it is also a special case of the vector autoregressive model (VAR), which consists of a system of more than one interlocking stochastic difference equation in more than one evolving random variable.

Scale-space theory is a framework for multi-scale signal representation developed by the computer vision, image processing and signal processing communities with complementary motivations from physics and biological vision. It is a formal theory for handling image structures at different scales, by representing an image as a one-parameter family of smoothed images, the scale-space representation, parametrized by the size of the smoothing kernel used for suppressing fine-scale structures. The parameter $in this family is referred to as the scale parameter, with the interpretation that image structures of spatial size smaller than about have largely been smoothed away in the scale-space level at scale .$

In Bayesian probability, the Jeffreys prior, named after Sir Harold Jeffreys, is a non-informative (objective) prior distribution for a parameter space; it is proportional to the square root of the determinant of the Fisher information matrix:

In imaging science, difference of Gaussians (DoG) is a feature enhancement algorithm that involves the subtraction of one blurred version of an original image from another, less blurred version of the original. In the simple case of grayscale images, the blurred images are obtained by convolving the original grayscale images with Gaussian kernels having differing standard deviations. Blurring an image using a Gaussian kernel suppresses only high-frequency spatial information. Subtracting one image from the other preserves spatial information that lies between the range of frequencies that are preserved in the two blurred images. Thus, the difference of Gaussians is a band-pass filter that discards all but a handful of spatial frequencies that are present in the original grayscale image.

The spectro-temporal receptive field or spatio-temporal receptive field (STRF) of a neuron represents which types of stimuli excite or inhibit that neuron. "Spectro-temporal" refers most commonly to audition, where the neuron's response depends on frequency versus time, while "spatio-temporal" refers to vision, where the neuron's response depends on spatial location versus time. Thus they are not exactly the same concept, but both referred to as STRF and serving a similar role in the analysis of neural responses.

In mathematics, parabolic cylindrical coordinates are a three-dimensional orthogonal coordinate system that results from projecting the two-dimensional parabolic coordinate system in the perpendicular $-direction. Hence, the coordinate surfaces are confocal parabolic cylinders. Parabolic cylindrical coordinates have found many applications, e.g., the potential theory of edges.$

Prolate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the focal axis of the ellipse, i.e., the symmetry axis on which the foci are located. Rotation about the other axis produces oblate spheroidal coordinates. Prolate spheroidal coordinates can also be considered as a limiting case of ellipsoidal coordinates in which the two smallest principal axes are equal in length.

In image processing and computer vision, a scale space framework can be used to represent an image as a family of gradually smoothed images. This framework is very general and a variety of scale space representations exist. A typical approach for choosing a particular type of scale space representation is to establish a set of scale-space axioms, describing basic properties of the desired scale-space representation and often chosen so as to make the representation useful in practical applications. Once established, the axioms narrow the possible scale-space representations to a smaller class, typically with only a few free parameters.

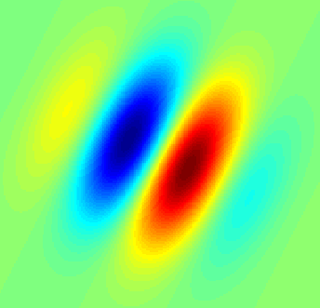
A simple cell in the primary visual cortex is a cell that responds primarily to oriented edges and gratings. These cells were discovered by Torsten Wiesel and David Hubel in the late 1950s.

In computer vision, blob detection methods are aimed at detecting regions in a digital image that differ in properties, such as brightness or color, compared to surrounding regions. Informally, a blob is a region of an image in which some properties are constant or approximately constant; all the points in a blob can be considered in some sense to be similar to each other. The most common method for blob detection is convolution.

Affine shape adaptation is a methodology for iteratively adapting the shape of the smoothing kernels in an affine group of smoothing kernels to the local image structure in neighbourhood region of a specific image point. Equivalently, affine shape adaptation can be accomplished by iteratively warping a local image patch with affine transformations while applying a rotationally symmetric filter to the warped image patches. Provided that this iterative process converges, the resulting fixed point will be affine invariant. In the area of computer vision, this idea has been used for defining affine invariant interest point operators as well as affine invariant texture analysis methods.

Filtering in the context of large eddy simulation (LES) is a mathematical operation intended to remove a range of small scales from the solution to the Navier-Stokes equations. Because the principal difficulty in simulating turbulent flows comes from the wide range of length and time scales, this operation makes turbulent flow simulation cheaper by reducing the range of scales that must be resolved. The LES filter operation is low-pass, meaning it filters out the scales associated with high frequencies.

Lagrangian field theory is a formalism in classical field theory. It is the field-theoretic analogue of Lagrangian mechanics. Lagrangian mechanics is used for discrete particles each with a finite number of degrees of freedom. Lagrangian field theory applies to continua and fields, which have an infinite number of degrees of freedom.

References

↑ D. Hubel and T. N. Wiesel (1959) "Receptive field of single neurons in the cat’s striate cortex", J Physiol 147, 226–238.
↑ D. Hubel and T. N. Wiesel (2005) Brain and Visual Perception: The Story of a 25-Year Collaboration. Oxford University Press.
1 2 G. C. DeAngelis, I. Ohzawa and R. D. Freeman (1995) "Receptive field dynamics in the central visual pathways". Trends Neurosci. 18(10), 451–457.
1 2 G. C. DeAngelis and A. Anzai (2004) "A modern view of the classical receptive field: linear and non-linear spatio-temporal processing by V1 neurons. In: Chalupa, L.M., Werner, J.S. (eds.) The Visual Neurosciences, vol. 1, pp. 704–719. MIT Press, Cambridge.
↑ B. R. Conway and M. S. Livingstone (2006) "Spatial and temporal properties of cone signals in alert macaque primary visual cortex", The Journal of Neuroscience 26(42): 10826-10846.
↑ L. M. Miller, N. A. Escabi, H. L. Read and C. Schreiber (2001) "Spectrotemporal receptive fields in the lemniscal auditory thalamus and cortex". J. Neurophys. 87:516-527.
↑ A. Qiu, C. E. Schreiber and M.A. Escape (2003) "Gabor analysis of auditory midbrain receptive fields: Spectro-temporal and binaural composition", Journal of Neurophysiology 90: 456-476.
↑ M. Elhilali, J. Fritz, T. S. Chi and S. Shamma (2007) "Auditory cortical receptive fields: Stable entities with plastic abilities", Journal of Neuroscience 27: 10372-10382.
↑ C. A. Atencio and C. E. Schreiber (2012) "Spectrotemporal processing in spectral tuning modules of cat primary auditory cortex", PLOS ONE 7:e31537.
1 2 3 4 5 T. Lindeberg (2013) "A computational theory of visual receptive fields", Biological Cybernetics, 107(6): 589-635.
1 2 3 4 T. Lindeberg (2016) "Time-causal and time-recursive spatio-temporal receptive fields", Journal of Mathematical Imaging and Vision 55(1): 50-88.
1 2 T. Lindeberg (2011) "Generalized Gaussian scale-space axiomatics comprising linear scale-space, affine scale-space and spatio-temporal scale-space", Journal of Mathematical Imaging and Vision, 40(1): 36-81.
↑ J. J. Koenderink and A. J. van Doorn (1987) "Representation of local geometry in the visual system", Biological Cybernetics 55:367–375.
↑ R. A. Young (1987) "The Gaussian derivative model for spatial vision: I. Retinal mechanisms", Spatial Vision 2(4): 273-293.
↑ J. J. Koenderink and A. J. van Doorn (1992) "Generic neighbourhood operators", IEEE Transactions on Pattern Analysis and Machine Intelligence, 14: 597-605.
↑ T. Lindeberg (1993) Scale-Space Theory in Computer Vision, Springer, 1993, ISBN 0-7923-9418-6.
↑ T. Lindeberg (1994). "Scale-space theory: A basic tool for analysing structures at different scales". Journal of Applied Statistics. 21 (2). pp. 224–270. doi:10.1080/757582976.
1 2 3 T. Lindeberg (2013) "Invariance of visual operations at the level of receptive fields", PLOS ONE 8(7): e66990, pages 1-33.
1 2 3 T. Lindeberg and A. Friberg (2015) "Idealized computational models of auditory receptive fields", PLOS ONE, 10(3): e0119032, pages 1-58.
1 2 3 T. Lindeberg and A. Friberg (2015) "Scale-space theory for auditory signals", Proc. SSVM 2015: Scale-Space and Variational Methods in Computer Vision, Springer LNCS 9087: 3-15.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[HubWie59-1] D. Hubel and T. N. Wiesel (1959) "Receptive field of single neurons in the cat’s striate cortex", J Physiol 147, 226–238.

[HubWie05-2] D. Hubel and T. N. Wiesel (2005) Brain and Visual Perception: The Story of a 25-Year Collaboration. Oxford University Press.

[DeAng95-3] 1 2 G. C. DeAngelis, I. Ohzawa and R. D. Freeman (1995) "Receptive field dynamics in the central visual pathways". Trends Neurosci. 18(10), 451–457.

[DeAng04-4] 1 2 G. C. DeAngelis and A. Anzai (2004) "A modern view of the classical receptive field: linear and non-linear spatio-temporal processing by V1 neurons. In: Chalupa, L.M., Werner, J.S. (eds.) The Visual Neurosciences, vol. 1, pp. 704–719. MIT Press, Cambridge.

[ConLiv06-5] B. R. Conway and M. S. Livingstone (2006) "Spatial and temporal properties of cone signals in alert macaque primary visual cortex", The Journal of Neuroscience 26(42): 10826-10846.

[MilEscReaSch01-6] L. M. Miller, N. A. Escabi, H. L. Read and C. Schreiber (2001) "Spectrotemporal receptive fields in the lemniscal auditory thalamus and cortex". J. Neurophys. 87:516-527.

[QiuSchEsc03-7] A. Qiu, C. E. Schreiber and M.A. Escape (2003) "Gabor analysis of auditory midbrain receptive fields: Spectro-temporal and binaural composition", Journal of Neurophysiology 90: 456-476.

[ElhFriChiSha07-8] M. Elhilali, J. Fritz, T. S. Chi and S. Shamma (2007) "Auditory cortical receptive fields: Stable entities with plastic abilities", Journal of Neuroscience 27: 10372-10382.

[9] C. A. Atencio and C. E. Schreiber (2012) "Spectrotemporal processing in spectral tuning modules of cat primary auditory cortex", PLOS ONE 7:e31537.

[Lin13BICY-10] 1 2 3 4 5 T. Lindeberg (2013) "A computational theory of visual receptive fields", Biological Cybernetics, 107(6): 589-635.

[Lin16-JMIV-11] 1 2 3 4 T. Lindeberg (2016) "Time-causal and time-recursive spatio-temporal receptive fields", Journal of Mathematical Imaging and Vision 55(1): 50-88.

[Lin11JMIV-12] 1 2 T. Lindeberg (2011) "Generalized Gaussian scale-space axiomatics comprising linear scale-space, affine scale-space and spatio-temporal scale-space", Journal of Mathematical Imaging and Vision, 40(1): 36-81.

[KoeDoo87-13] J. J. Koenderink and A. J. van Doorn (1987) "Representation of local geometry in the visual system", Biological Cybernetics 55:367–375.

[You87-14] R. A. Young (1987) "The Gaussian derivative model for spatial vision: I. Retinal mechanisms", Spatial Vision 2(4): 273-293.

[KoeDoo92-15] J. J. Koenderink and A. J. van Doorn (1992) "Generic neighbourhood operators", IEEE Transactions on Pattern Analysis and Machine Intelligence, 14: 597-605.

[lin94-16] T. Lindeberg (1993) Scale-Space Theory in Computer Vision, Springer, 1993, ISBN 0-7923-9418-6.

[lin94review-17] T. Lindeberg (1994). "Scale-space theory: A basic tool for analysing structures at different scales". Journal of Applied Statistics. 21 (2). pp. 224–270. doi:10.1080/757582976.

[Lin13PONE-18] 1 2 3 T. Lindeberg (2013) "Invariance of visual operations at the level of receptive fields", PLOS ONE 8(7): e66990, pages 1-33.

[LinFri15PONE-19] 1 2 3 T. Lindeberg and A. Friberg (2015) "Idealized computational models of auditory receptive fields", PLOS ONE, 10(3): e0119032, pages 1-58.

[LinFri15SSVM-20] 1 2 3 T. Lindeberg and A. Friberg (2015) "Scale-space theory for auditory signals", Proc. SSVM 2015: Scale-Space and Variational Methods in Computer Vision, Springer LNCS 9087: 3-15.