In graph theory, the girth of an undirected graph is the length of a shortest cycle contained in the graph. If the graph does not contain any cycles, its girth is defined to be infinity. For example, a 4-cycle (square) has girth 4. A grid has girth 4 as well, and a triangular mesh has girth 3. A graph with girth four or more is triangle-free.

In the mathematical field of graph theory, the Tutte–Coxeter graph or Tutte eight-cage or Cremona–Richmond graph is a 3-regular graph with 30 vertices and 45 edges. As the unique smallest cubic graph of girth 8, it is a cage and a Moore graph. It is bipartite, and can be constructed as the Levi graph of the generalized quadrangle W2. The graph is named after William Thomas Tutte and H. S. M. Coxeter; it was discovered by Tutte (1947) but its connection to geometric configurations was investigated by both authors in a pair of jointly published papers.

In the mathematical field of graph theory, a cage is a regular graph that has as few vertices as possible for its girth.

In the mathematical field of graph theory, the odd graphs are a family of symmetric graphs defined from certain set systems. They include and generalize the Petersen graph.

In the mathematical field of graph theory, the Harries graph or Harries (3-10)-cage is a 3-regular, undirected graph with 70 vertices and 105 edges.
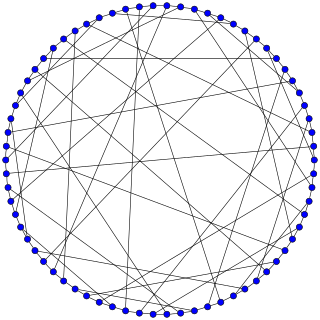
In the mathematical field of graph theory, the Harries–Wong graph is a 3-regular undirected graph with 70 vertices and 105 edges.

In the mathematical field of graph theory, the Balaban 10-cage or Balaban (3,10)-cage is a 3-regular graph with 70 vertices and 105 edges named after Alexandru T. Balaban. Published in 1972, It was the first 10-cage discovered but it is not unique.

In the mathematical field of graph theory, the McGee graph or the (3-7)-cage is a 3-regular graph with 24 vertices and 36 edges.

In the mathematical field of graph theory, the Frucht graph is a cubic graph with 12 vertices, 18 edges, and no nontrivial symmetries. It was first described by Robert Frucht in 1939.

In the mathematical field of graph theory, the Biggs–Smith graph is a 3-regular graph with 102 vertices and 153 edges.

In the mathematical field of graph theory, the Dyck graph is a 3-regular graph with 32 vertices and 48 edges, named after Walther von Dyck.

In the mathematical field of graph theory, the Blanuša snarks are two 3-regular graphs with 18 vertices and 27 edges. They were discovered by Yugoslavian mathematician Danilo Blanuša in 1946 and are named after him. When discovered, only one snark was known—the Petersen graph.
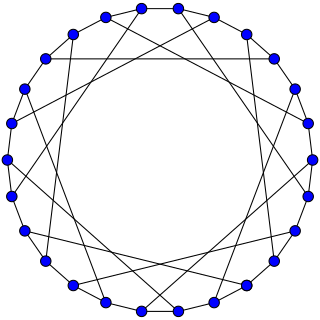
In the mathematical field of graph theory, the F26A graph is a symmetric bipartite cubic graph with 26 vertices and 39 edges.

In the mathematical field of graph theory, the Robertson graph or (4,5)-cage, is a 4-regular undirected graph with 19 vertices and 38 edges named after Neil Robertson.
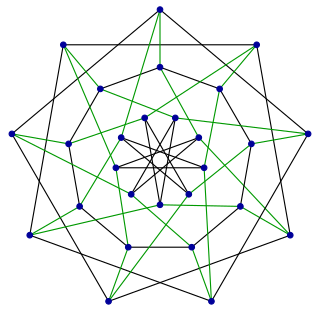
In graph theory, the Holt graph or Doyle graph is the smallest half-transitive graph, that is, the smallest example of a vertex-transitive and edge-transitive graph which is not also symmetric. Such graphs are not common. It is named after Peter G. Doyle and Derek F. Holt, who discovered the same graph independently in 1976 and 1981 respectively.

In the mathematical field of graph theory, the Tutte 12-cage or Benson graph is a 3-regular graph with 126 vertices and 189 edges. It is named after W. T. Tutte.
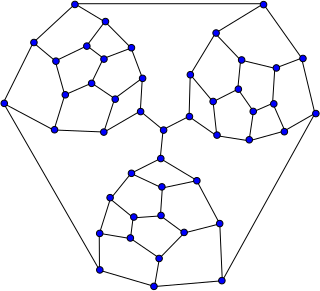
In the mathematical field of graph theory, the Tutte graph is a 3-regular graph with 46 vertices and 69 edges named after W. T. Tutte. It has chromatic number 3, chromatic index 3, girth 4 and diameter 8.

The 110-vertex Iofinova–Ivanov graph is, in graph theory, a semi-symmetric cubic graph with 110 vertices and 165 edges.

In the mathematical field of graph theory, the Robertson–Wegner graph is a 5-regular undirected graph with 30 vertices and 75 edges named after Neil Robertson and Gerd Wegner.

In the mathematical field of graph theory, the Foster cage is a 5-regular undirected graph with 30 vertices and 75 edges. It is one of the four (5,5)-cage graphs, the others being the Meringer graph, the Robertson–Wegner graph, and the Wong graph.
























