
In geometry, the circumference is the perimeter of a circle or ellipse. That is, the circumference would be the arc length of the circle, as if it were opened up and straightened out to a line segment. More generally, the perimeter is the curve length around any closed figure. Circumference may also refer to the circle itself, that is, the locus corresponding to the edge of a disk. The circumference of a sphere is the circumference, or length, of any one of its great circles.

In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circle. It can also be defined as the longest chord of the circle. Both definitions are also valid for the diameter of a sphere.

Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's approach consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated earlier, Euclid was the first to organize these propositions into a logical system in which each result is proved from axioms and previously proved theorems.
In geometry, a polygon is a plane figure that is described by a finite number of straight line segments connected to form a closed polygonal chain. The bounded plane region, the bounding circuit, or the two together, may be called a polygon.

Ancient Greek architecture came from the Greek-speaking people whose culture flourished on the Greek mainland, the Peloponnese, the Aegean Islands, and in colonies in Anatolia and Italy for a period from about 900 BC until the 1st century AD, with the earliest remaining architectural works dating from around 600 BC.

In elementary geometry, two geometric objects are perpendicular if they intersect at a right angle.

The Ionic order is one of the three canonic orders of classical architecture, the other two being the Doric and the Corinthian. There are two lesser orders: the Tuscan, and the rich variant of Corinthian called the composite order. Of the three classical canonic orders, the Corinthian order has the narrowest columns, followed by the Ionic order, with the Doric order having the widest columns.

Apollonius of Perga was an Ancient Greek geometer and astronomer known for his work on conic sections. Beginning from the contributions of Euclid and Archimedes on the topic, he brought them to the state prior to the invention of analytic geometry. His definitions of the terms ellipse, parabola, and hyperbola are the ones in use today. Gottfried Wilhelm Leibniz stated “He who understands Archimedes and Apollonius will admire less the achievements of the foremost men of later times.”

In geometry, a prism is a polyhedron comprising an n-sided polygon base, a second base which is a translated copy of the first, and n other faces, necessarily all parallelograms, joining corresponding sides of the two bases. All cross-sections parallel to the bases are translations of the bases. Prisms are named after their bases, e.g. a prism with a pentagonal base is called a pentagonal prism. Prisms are a subclass of prismatoids.

In geometry, a star polygon is a type of non-convex polygon, and most commonly, a type of decagon. Regular star polygons have been studied in depth; while star polygons in general appear not to have been formally defined, however certain notable ones can arise through truncation operations on regular simple and star polygons.

In geometry, a diagonal is a line segment joining two vertices of a polygon or polyhedron, when those vertices are not on the same edge. Informally, any sloping line is called diagonal. The word diagonal derives from the ancient Greek διαγώνιος diagonios, "from angle to angle" ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a rhombus or cuboid, and later adopted into Latin as diagonus.

Ancient Greek pottery, due to its relative durability, comprises a large part of the archaeological record of ancient Greece, and since there is so much of it, it has exerted a disproportionately large influence on our understanding of Greek society. The shards of pots discarded or buried in the 1st millennium BC are still the best guide available to understand the customary life and mind of the ancient Greeks. There were several vessels produced locally for everyday and kitchen use, yet finer pottery from regions such as Attica was imported by other civilizations throughout the Mediterranean, such as the Etruscans in Italy. There were a multitude of specific regional varieties, such as the South Italian ancient Greek pottery.
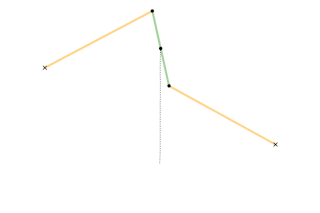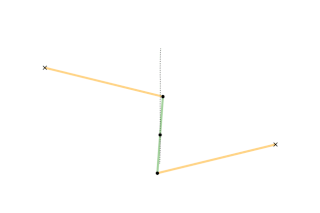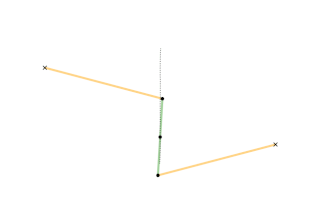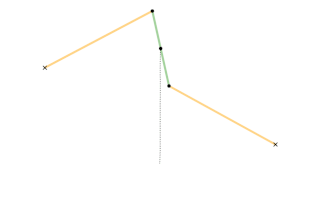
Watt's linkage is a type of mechanical linkage invented by James Watt in which the central moving point of the linkage is constrained to travel on a nearly straight line. It was described in Watt's patent specification of 1784 for the Watt steam engine.

A skyphos is a two-handled deep wine-cup on a low flanged base or none. The handles may be horizontal ear-shaped thumbholds that project from the rim, or they may be loop handles at the rim or that stand away from the lower part of the body. Skyphoi of the type called glaux (owl) have one horizontal and one vertical thumbhold handle.

Many shapes have metaphorical names, i.e., their names are metaphors: these shapes are named after a most common object that has it. For example, "U-shape" is a shape that resembles the letter U, a bell-shaped curve has the shape of the vertical cross-section of a bell, etc. These terms may variously refer to objects, their cross sections or projections.

In fractal geometry, the H tree, or T-branching, is a fractal tree structure constructed from perpendicular line segments, each smaller by a factor of the square root of 2 from the next larger adjacent segment. It is so called because its repeating pattern resembles the letter "H". It has Hausdorff dimension 2, and comes arbitrarily close to every point in a rectangle. Its applications include VLSI design and microwave engineering.

Geometry is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space that are related with distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a geometer.
In string theory and related theories such as supergravity theories, a brane is a physical object that generalizes the notion of a point particle to higher dimensions. Branes are dynamical objects which can propagate through spacetime according to the rules of quantum mechanics. They have mass and can have other attributes such as charge.

Egyptian geometry refers to geometry as it was developed and used in Ancient Egypt. Their geometry was a necessary outgrowth of surveying to preserve the layout and ownership of farmland, which was flooded annually by the Nile river.

Dipylon kraters are Geometric Period Greek terracotta funerary vases found at the Dipylon cemetery; near the Dipylon Gate, in Kerameikos. Kerameikos is known as the ancient potters quarter on the northwest side of the ancient city of Athens and translates to "the city of clay." A krater is a large Ancient Greek painted vase used to mix wine and water, but the large kraters at the Dipylon cemetery served as grave markers.

















