This article only references primary sources.(January 2023) |
Barsoum elements is a finite element analysis technique used in fracture analysis to determine the stress intensity factor of a crack. It was introduced by R. Barsoum in 1976. [1]
This article only references primary sources.(January 2023) |
Barsoum elements is a finite element analysis technique used in fracture analysis to determine the stress intensity factor of a crack. It was introduced by R. Barsoum in 1976. [1]
In this method, the usual isoparametric 6 node triangular or 8 node isoparametric quadrilateral elements are employed. The mid side nodes on 2 adjacent sides are shifted towards the corner node to the quarter point location. For these locations of the mid nodes, the Jacobian becomes singular at the corner node thus making displacement derivatives infinite and stresses and strains become infinite as well. It can be shown that the variation of stresses along the 2 sides of the elements is according to 1/√r.
On the other hand, if all the three nodes on the side of an 8 node quadrilateral element are collapsed to one node (given the same node number) then the stress or strain varies as 1/√r along any radial line emanating from crack tip. All the mid side nodes adjacent to the crack tip are at quarter point locations. From the displacement field solution the stress intensity factor K1 in a mode 1 case can be calculated as per the following relation:
where VB and VC are the displacement in the y direction behind the crack tip.
It has been demonstrated that K1 found by this method is within 2% of theoretical solutions. Accuracy of finite element calculation can be improved if the neighboring elements are also modeled to have the terms depicting the stresses for a crack with its tip outside the element.
Structural analysis is a branch of solid mechanics which uses simplified models for solids like bars, beams and shells for engineering decision making. Its main objective is to determine the effect of loads on the physical structures and their components. In contrast to theory of elasticity, the models used in structure analysis are often differential equations in one spatial variable. Structures subject to this type of analysis include all that must withstand loads, such as buildings, bridges, aircraft and ships. Structural analysis uses ideas from applied mechanics, materials science and applied mathematics to compute a structure's deformations, internal forces, stresses, support reactions, velocity, accelerations, and stability. The results of the analysis are used to verify a structure's fitness for use, often precluding physical tests. Structural analysis is thus a key part of the engineering design of structures.

In solid mechanics, a stress concentration is a location in an object where the stress is significantly greater than the surrounding region. Stress concentrations occur when there are irregularities in the geometry or material of a structural component that cause an interruption to the flow of stress. This arises from such details as holes, grooves, notches and fillets. Stress concentrations may also occur from accidental damage such as nicks and scratches.
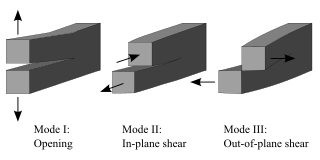
Fracture mechanics is the field of mechanics concerned with the study of the propagation of cracks in materials. It uses methods of analytical solid mechanics to calculate the driving force on a crack and those of experimental solid mechanics to characterize the material's resistance to fracture.
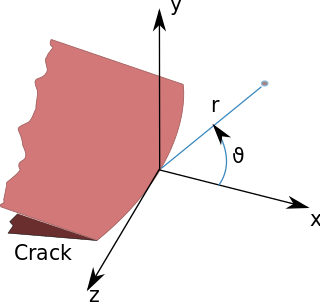
In fracture mechanics, the stress intensity factor is used to predict the stress state near the tip of a crack or notch caused by a remote load or residual stresses. It is a theoretical construct usually applied to a homogeneous, linear elastic material and is useful for providing a failure criterion for brittle materials, and is a critical technique in the discipline of damage tolerance. The concept can also be applied to materials that exhibit small-scale yielding at a crack tip.
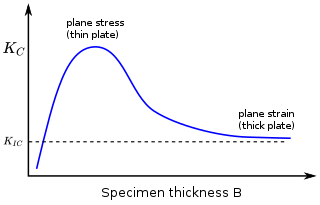
In materials science, fracture toughness is the critical stress intensity factor of a sharp crack where propagation of the crack suddenly becomes rapid and unlimited. A component's thickness affects the constraint conditions at the tip of a crack with thin components having plane stress conditions and thick components having plane strain conditions. Plane strain conditions give the lowest fracture toughness value which is a material property. The critical value of stress intensity factor in mode I loading measured under plane strain conditions is known as the plane strain fracture toughness, denoted . When a test fails to meet the thickness and other test requirements that are in place to ensure plane strain conditions, the fracture toughness value produced is given the designation . Fracture toughness is a quantitative way of expressing a material's resistance to crack propagation and standard values for a given material are generally available.
The finite element method (FEM) is a powerful technique originally developed for numerical solution of complex problems in structural mechanics, and it remains the method of choice for complex systems. In the FEM, the structural system is modeled by a set of appropriate finite elements interconnected at discrete points called nodes. Elements may have physical properties such as thickness, coefficient of thermal expansion, density, Young's modulus, shear modulus and Poisson's ratio.

The three-point bending flexural test provides values for the modulus of elasticity in bending , flexural stress , flexural strain and the flexural stress–strain response of the material. This test is performed on a universal testing machine with a three-point or four-point bend fixture. The main advantage of a three-point flexural test is the ease of the specimen preparation and testing. However, this method has also some disadvantages: the results of the testing method are sensitive to specimen and loading geometry and strain rate.
The J-integral represents a way to calculate the strain energy release rate, or work (energy) per unit fracture surface area, in a material. The theoretical concept of J-integral was developed in 1967 by G. P. Cherepanov and independently in 1968 by James R. Rice, who showed that an energetic contour path integral was independent of the path around a crack.
AFGROW is a Damage Tolerance Analysis (DTA) computer program that calculates crack initiation, fatigue crack growth, and fracture to predict the life of metallic structures. Originally developed by the Air Force Research Laboratory, AFGROW is mainly used for aerospace applications, but can be applied to any type of metallic structure that experiences fatigue cracking.

The extended finite element method (XFEM), is a numerical technique based on the generalized finite element method (GFEM) and the partition of unity method (PUM). It extends the classical finite element method (FEM) approach by enriching the solution space for solutions to differential equations with discontinuous functions.
Material failure theory is an interdisciplinary field of materials science and solid mechanics which attempts to predict the conditions under which solid materials fail under the action of external loads. The failure of a material is usually classified into brittle failure (fracture) or ductile failure (yield). Depending on the conditions most materials can fail in a brittle or ductile manner or both. However, for most practical situations, a material may be classified as either brittle or ductile.
In fracture mechanics, the energy release rate, , is the rate at which energy is transformed as a material undergoes fracture. Mathematically, the energy release rate is expressed as the decrease in total potential energy per increase in fracture surface area, and is thus expressed in terms of energy per unit area. Various energy balances can be constructed relating the energy released during fracture to the energy of the resulting new surface, as well as other dissipative processes such as plasticity and heat generation. The energy release rate is central to the field of fracture mechanics when solving problems and estimating material properties related to fracture and fatigue.

A compact tension specimen (CT) is a type of standard notched specimen in accordance with ASTM and ISO standards. Compact tension specimens are used extensively in the area of fracture mechanics and corrosion testing, in order to establish fracture toughness and fatigue crack growth data for a material.
James C. Newman is an American engineer and materials scientist known for his work on fracture and fatigue for aerospace vehicles. NASA has listed him as a "Superstar of Modern Aeronautics".
Smoothed finite element methods (S-FEM) are a particular class of numerical simulation algorithms for the simulation of physical phenomena. It was developed by combining meshfree methods with the finite element method. S-FEM are applicable to solid mechanics as well as fluid dynamics problems, although so far they have mainly been applied to the former.
Weakened weak form is used in the formulation of general numerical methods based on meshfree methods and/or finite element method settings. These numerical methods are applicable to solid mechanics as well as fluid dynamics problems.
Concrete is widely used construction material all over the world. It is composed of aggregate, cement and water. Composition of concrete varies to suit for different applications desired. Even size of the aggregate can influence mechanical properties of concrete to a great extent.

Crack tip opening displacement (CTOD) or is the distance between the opposite faces of a crack tip at the 90° intercept position. The position behind the crack tip at which the distance is measured is arbitrary but commonly used is the point where two 45° lines, starting at the crack tip, intersect the crack faces. The parameter is used in fracture mechanics to characterize the loading on a crack and can be related to other crack tip loading parameters such as the stress intensity factor and the elastic-plastic J-integral.
The fracture of soft materials involves large deformations and crack blunting before propagation of the crack can occur. Consequently, the stress field close to the crack tip is significantly different from the traditional formulation encountered in the Linear elastic fracture mechanics. Therefore, fracture analysis for these applications requires a special attention. The Linear Elastic Fracture Mechanics (LEFM) and K-field are based on the assumption of infinitesimal deformation, and as a result are not suitable to describe the fracture of soft materials. However, LEFM general approach can be applied to understand the basics of fracture on soft materials. The solution for the deformation and crack stress field in soft materials considers large deformation and is derived from the finite strain elastostatics framework and hyperelastic material models.

A crack growth equation is used for calculating the size of a fatigue crack growing from cyclic loads. The growth of fatigue cracks can result in catastrophic failure, particularly in the case of aircraft. A crack growth equation can be used to ensure safety, both in the design phase and during operation, by predicting the size of cracks. In critical structure, loads can be recorded and used to predict the size of cracks to ensure maintenance or retirement occurs prior to any of the cracks failing.