Related Research Articles

In geometry, the convex hull or convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, or equivalently as the set of all convex combinations of points in the subset. For a bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around the subset.

Linear programming (LP), also called linear optimization, is a method to achieve the best outcome in a mathematical model whose requirements are represented by linear relationships. Linear programming is a special case of mathematical programming.
The Nash embedding theorems, named after John Forbes Nash Jr., state that every Riemannian manifold can be isometrically embedded into some Euclidean space. Isometric means preserving the length of every path. For instance, bending but neither stretching nor tearing a page of paper gives an isometric embedding of the page into Euclidean space because curves drawn on the page retain the same arclength however the page is bent.

Mathematical optimization or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries.
The principle of maximum entropy states that the probability distribution which best represents the current state of knowledge about a system is the one with largest entropy, in the context of precisely stated prior data.

In differential calculus and differential geometry, an inflection point, point of inflection, flex, or inflection is a point on a smooth plane curve at which the curvature changes sign. In particular, in the case of the graph of a function, it is a point where the function changes from being concave to convex, or vice versa.
In mathematical analysis, in particular the subfields of convex analysis and optimization, a proper convex function is an extended real-valued convex function with a non-empty domain, that never takes on the value and also is not identically equal to
Pontryagin's maximum principle is used in optimal control theory to find the best possible control for taking a dynamical system from one state to another, especially in the presence of constraints for the state or input controls. It states that it is necessary for any optimal control along with the optimal state trajectory to solve the so-called Hamiltonian system, which is a two-point boundary value problem, plus a maximum condition of the control Hamiltonian. These necessary conditions become sufficient under certain convexity conditions on the objective and constraint functions.

In geometry, Radon's theorem on convex sets, published by Johann Radon in 1921, states that:
Any set of d + 2 points in Rd can be partitioned into two sets whose convex hulls intersect.
In the mathematical field of partial differential equations, Harnack's principle or Harnack's theorem is a corollary of Harnack's inequality which deals with the convergence of sequences of harmonic functions.
In the mathematical fields of partial differential equations and geometric analysis, the maximum principle is any of a collection of results and techniques of fundamental importance in the study of elliptic and parabolic differential equations.
In mathematics, Fenchel's duality theorem is a result in the theory of convex functions named after Werner Fenchel.
In mathematical optimization theory, duality or the duality principle is the principle that optimization problems may be viewed from either of two perspectives, the primal problem or the dual problem. If the primal is a minimization problem then the dual is a maximization problem. Any feasible solution to the primal (minimization) problem is at least as large as any feasible solution to the dual (maximization) problem. Therefore, the solution to the primal is an upper bound to the solution of the dual, and the solution of the dual is a lower bound to the solution of the primal. This fact is called weak duality.
In mathematics, a quasiconvex function is a real-valued function defined on an interval or on a convex subset of a real vector space such that the inverse image of any set of the form is a convex set. For a function of a single variable, along any stretch of the curve the highest point is one of the endpoints. The negative of a quasiconvex function is said to be quasiconcave.
The maximum theorem provides conditions for the continuity of an optimized function and the set of its maximizers with respect to its parameters. The statement was first proven by Claude Berge in 1959. The theorem is primarily used in mathematical economics and optimal control.

In geometry, a convex curve is a plane curve that has a supporting line through each of its points. There are many other equivalent definitions of these curves, going back to Archimedes. Examples of convex curves include the convex polygons, the boundaries of convex sets, and the graphs of convex functions. Important subclasses of convex curves include the closed convex curves, the smooth curves that are convex, and the strictly convex curves, which have the additional property that each supporting line passes through a unique point of the curve.
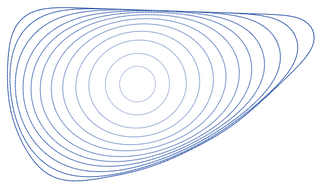
In mathematics, the curve-shortening flow is a process that modifies a smooth curve in the Euclidean plane by moving its points perpendicularly to the curve at a speed proportional to the curvature. The curve-shortening flow is an example of a geometric flow, and is the one-dimensional case of the mean curvature flow. Other names for the same process include the Euclidean shortening flow, geometric heat flow, and arc length evolution.

Most of the terms listed in Wikipedia glossaries are already defined and explained within Wikipedia itself. However, glossaries like this one are useful for looking up, comparing and reviewing large numbers of terms together. You can help enhance this page by adding new terms or writing definitions for existing ones.
In discrete mathematics, a discrete fixed-point is a fixed-point for functions defined on finite sets, typically subsets of the integer grid .
References
- ↑ Bauer, Heinz (1958-11-01). "Minimalstellen von Funktionen und Extremalpunkte". Archiv der Mathematik (in German). 9 (4): 389–393. doi:10.1007/BF01898615. ISSN 1420-8938. S2CID 120811485.
- ↑ Kružík, Martin (2000-11-01). "Bauer's maximum principle and hulls of sets". Calculus of Variations and Partial Differential Equations. 11 (3): 321–332. doi:10.1007/s005260000047. ISSN 1432-0835. S2CID 122781793.
- ↑ Manelli, Alejandro M.; Vincent, Daniel R. (2007-11-01). "Multidimensional mechanism design: Revenue maximization and the multiple-good monopoly" (PDF). Journal of Economic Theory. 137 (1): 153–185. doi:10.1016/j.jet.2006.12.007. hdl: 10419/74262 . ISSN 0022-0531.[ permanent dead link ]