Molecular dynamics (MD) is a computer simulation method for analyzing the physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a fixed period of time, giving a view of the dynamic "evolution" of the system. In the most common version, the trajectories of atoms and molecules are determined by numerically solving Newton's equations of motion for a system of interacting particles, where forces between the particles and their potential energies are often calculated using interatomic potentials or molecular mechanical force fields. The method is applied mostly in chemical physics, materials science, and biophysics.
In mathematics, a symplectic integrator (SI) is a numerical integration scheme for Hamiltonian systems. Symplectic integrators form the subclass of geometric integrators which, by definition, are canonical transformations. They are widely used in nonlinear dynamics, molecular dynamics, discrete element methods, accelerator physics, plasma physics, quantum physics, and celestial mechanics.
Direct simulation Monte Carlo (DSMC) method uses probabilistic Monte Carlo simulation to solve the Boltzmann equation for finite Knudsen number fluid flows.
Virial stress is a measure of mechanical stress on an atomic scale for homogeneous systems. The expression of the (local) virial stress can be derived as the functional derivative of the free energy of a molecular system with respect to the deformation tensor.
Car–Parrinello molecular dynamics or CPMD refers to either a method used in molecular dynamics or the computational chemistry software package used to implement this method.
In computational chemistry, a water model is used to simulate and thermodynamically calculate water clusters, liquid water, and aqueous solutions with explicit solvent. The models are determined from quantum mechanics, molecular mechanics, experimental results, and these combinations. To imitate a specific nature of molecules, many types of models have been developed. In general, these can be classified by the following three points; (i) the number of interaction points called site, (ii) whether the model is rigid or flexible, (iii) whether the model includes polarization effects.
Path integral Monte Carlo (PIMC) is a quantum Monte Carlo method used to solve quantum statistical mechanics problems numerically within the path integral formulation. The application of Monte Carlo methods to path integral simulations of condensed matter systems was first pursued in a key paper by John A. Barker.
In molecular dynamics (MD) simulations, the flying ice cube effect is an artifact in which the energy of high-frequency fundamental modes is drained into low-frequency modes, particularly into zero-frequency motions such as overall translation and rotation of the system. The artifact derives its name from a particularly noticeable manifestation that arises in simulations of particles in vacuum, where the system being simulated acquires high linear momentum and experiences extremely damped internal motions, freezing the system into a single conformation reminiscent of an ice cube or other rigid body flying through space. The artifact is entirely a consequence of molecular dynamics algorithms and is wholly unphysical, since it violates the principle of equipartition of energy.
In computer simulations of mechanical systems, energy drift is the gradual change in the total energy of a closed system over time. According to the laws of mechanics, the energy should be a constant of motion and should not change. However, in simulations the energy might fluctuate on a short time scale and increase or decrease on a very long time scale due to numerical integration artifacts that arise with the use of a finite time step Δt. This is somewhat similar to the flying ice cube problem, whereby numerical errors in handling equipartition of energy can change vibrational energy into translational energy.
CP2K is a freely available (GPL) quantum chemistry and solid state physics program package, written in Fortran 2008, to perform atomistic simulations of solid state, liquid, molecular, periodic, material, crystal, and biological systems. It provides a general framework for different methods: density functional theory (DFT) using a mixed Gaussian and plane waves approach (GPW) via LDA, GGA, MP2, or RPA levels of theory, classical pair and many-body potentials, semi-empirical and tight-binding Hamiltonians, as well as Quantum Mechanics/Molecular Mechanics (QM/MM) hybrid schemes relying on the Gaussian Expansion of the Electrostatic Potential (GEEP). The Gaussian and Augmented Plane Waves method (GAPW) as an extension of the GPW method allows for all-electron calculations. CP2K can do simulations of molecular dynamics, metadynamics, Monte Carlo, Ehrenfest dynamics, vibrational analysis, core level spectroscopy, energy minimization, and transition state optimization using NEB or dimer method.
Desmond is a software package developed at D. E. Shaw Research to perform high-speed molecular dynamics simulations of biological systems on conventional computer clusters. The code uses novel parallel algorithms and numerical methods to achieve high performance on platforms containing multiple processors, but may also be executed on a single computer.
The Nosé–Hoover thermostat is a deterministic algorithm for constant-temperature molecular dynamics simulations. It was originally developed by Nosé and was improved further by Hoover. Although the heat bath of Nosé–Hoover thermostat consists of only one imaginary particle, simulation systems achieve realistic constant-temperature condition. Therefore, the Nosé–Hoover thermostat has been commonly used as one of the most accurate and efficient methods for constant-temperature molecular dynamics simulations.
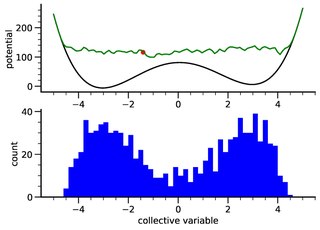
Metadynamics is a computer simulation method in computational physics, chemistry and biology. It is used to estimate the free energy and other state functions of a system, where ergodicity is hindered by the form of the system's energy landscape. It was first suggested by Alessandro Laio and Michele Parrinello in 2002 and is usually applied within molecular dynamics simulations. MTD closely resembles a number of newer methods such as adaptively biased molecular dynamics, adaptive reaction coordinate forces and local elevation umbrella sampling. More recently, both the original and well-tempered metadynamics were derived in the context of importance sampling and shown to be a special case of the adaptive biasing potential setting. MTD is related to the Wang–Landau sampling.
Michele Parrinello is an Italian physicist particularly known for his work in molecular dynamics. Parrinello and Roberto Car were awarded the Dirac Medal and the Sidney Fernbach Award in 2009 for their continuing development of the Car–Parrinello method, first proposed in their seminal 1985 paper, "Unified Approach for Molecular Dynamics and Density-Functional Theory". They have continued to receive awards for this breakthrough, most recently the Dreyfus Prize in the Chemical Sciences and the 2020 Benjamin Franklin Medal in Chemistry.
The Andersen thermostat is a proposal in molecular dynamics simulation for maintaining constant temperature conditions. It is based on periodic reassignment of the velocities of atoms or molecules. For each atom or molecule, the reassigned velocity is picked randomly according to Maxwell–Boltzmann statistics for the given temperature.
Shuichi Nosé was a Japanese physicist.
Surface hopping is a mixed quantum-classical technique that incorporates quantum mechanical effects into molecular dynamics simulations. Traditional molecular dynamics assume the Born-Oppenheimer approximation, where the lighter electrons adjust instantaneously to the motion of the nuclei. Though the Born-Oppenheimer approximation is applicable to a wide range of problems, there are several applications, such as photoexcited dynamics, electron transfer, and surface chemistry where this approximation falls apart. Surface hopping partially incorporates the non-adiabatic effects by including excited adiabatic surfaces in the calculations, and allowing for 'hops' between these surfaces, subject to certain criteria.
The prediction of crystal properties by numerical simulation has become commonplace in the last 20 years as computers have grown more powerful and theoretical techniques more sophisticated. High accuracy prediction of elastic, electronic, transport and phase properties is possible with modern methods.
Newton-X is a general program for molecular dynamics simulations beyond the Born-Oppenheimer approximation. It has been primarily used for simulations of ultrafast processes in photoexcited molecules. It has also been used for simulation of band envelops of absorption and emission spectra.
Qbox is an open-source software package for atomic-scale simulations of molecules, liquids and solids. It implements first principles molecular dynamics, a simulation method in which inter-atomic forces are derived from quantum mechanics. Qbox is released under a GNU General Public License (GPL) with documentation provided at http://qboxcode.org. It is available as a FreeBSD port.
