Related Research Articles
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. It does not assume or postulate any natural laws, but explains the macroscopic behavior of nature from the behavior of such ensembles.

Molecular dynamics (MD) is a computer simulation method for analyzing the physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a fixed period of time, giving a view of the dynamic "evolution" of the system. In the most common version, the trajectories of atoms and molecules are determined by numerically solving Newton's equations of motion for a system of interacting particles, where forces between the particles and their potential energies are often calculated using interatomic potentials or molecular mechanical force fields. The method is applied mostly in chemical physics, materials science, and biophysics.

In classical statistical mechanics, the equipartition theorem relates the temperature of a system to its average energies. The equipartition theorem is also known as the law of equipartition, equipartition of energy, or simply equipartition. The original idea of equipartition was that, in thermal equilibrium, energy is shared equally among all of its various forms; for example, the average kinetic energy per degree of freedom in translational motion of a molecule should equal that in rotational motion.
In statistical mechanics, the microcanonical ensemble is a statistical ensemble that represents the possible states of a mechanical system whose total energy is exactly specified. The system is assumed to be isolated in the sense that it cannot exchange energy or particles with its environment, so that the energy of the system does not change with time.
A property of a physical system, such as the entropy of a gas, that stays approximately constant when changes occur slowly is called an adiabatic invariant. By this it is meant that if a system is varied between two end points, as the time for the variation between the end points is increased to infinity, the variation of an adiabatic invariant between the two end points goes to zero.
In physics, Langevin dynamics is an approach to the mathematical modeling of the dynamics of molecular systems. It was originally developed by French physicist Paul Langevin. The approach is characterized by the use of simplified models while accounting for omitted degrees of freedom by the use of stochastic differential equations. Langevin dynamics simulations are a kind of Monte Carlo simulation.
Car–Parrinello molecular dynamics or CPMD refers to either a method used in molecular dynamics or the computational chemistry software package used to implement this method.
Path integral Monte Carlo (PIMC) is a quantum Monte Carlo method used to solve quantum statistical mechanics problems numerically within the path integral formulation. The application of Monte Carlo methods to path integral simulations of condensed matter systems was first pursued in a key paper by John A. Barker.
In computer simulations of mechanical systems, energy drift is the gradual change in the total energy of a closed system over time. According to the laws of mechanics, the energy should be a constant of motion and should not change. However, in simulations the energy might fluctuate on a short time scale and increase or decrease on a very long time scale due to numerical integration artifacts that arise with the use of a finite time step Δt. This is somewhat similar to the flying ice cube problem, whereby numerical errors in handling equipartition of energy can change vibrational energy into translational energy.

Periodic boundary conditions (PBCs) are a set of boundary conditions which are often chosen for approximating a large (infinite) system by using a small part called a unit cell. PBCs are often used in computer simulations and mathematical models. The topology of two-dimensional PBC is equal to that of a world map of some video games; the geometry of the unit cell satisfies perfect two-dimensional tiling, and when an object passes through one side of the unit cell, it re-appears on the opposite side with the same velocity. In topological terms, the space made by two-dimensional PBCs can be thought of as being mapped onto a torus (compactification). The large systems approximated by PBCs consist of an infinite number of unit cells. In computer simulations, one of these is the original simulation box, and others are copies called images. During the simulation, only the properties of the original simulation box need to be recorded and propagated. The minimum-image convention is a common form of PBC particle bookkeeping in which each individual particle in the simulation interacts with the closest image of the remaining particles in the system.
The Berendsen thermostat is an algorithm to re-scale the velocities of particles in molecular dynamics simulations to control the simulation temperature.
Dissipative particle dynamics (DPD) is an off-lattice mesoscopic simulation technique which involves a set of particles moving in continuous space and discrete time. Particles represent whole molecules or fluid regions, rather than single atoms, and atomistic details are not considered relevant to the processes addressed. The particles' internal degrees of freedom are integrated out and replaced by simplified pairwise dissipative and random forces, so as to conserve momentum locally and ensure correct hydrodynamic behaviour. The main advantage of this method is that it gives access to longer time and length scales than are possible using conventional MD simulations. Simulations of polymeric fluids in volumes up to 100 nm in linear dimension for tens of microseconds are now common.
The demon algorithm is a Monte Carlo method for efficiently sampling members of a microcanonical ensemble with a given energy. An additional degree of freedom, called 'the demon', is added to the system and is able to store and provide energy. If a drawn microscopic state has lower energy than the original state, the excess energy is transferred to the demon. For a sampled state that has higher energy than desired, the demon provides the missing energy if it is available. The demon can not have negative energy and it does not interact with the particles beyond exchanging energy. Note that the additional degree of freedom of the demon does not alter a system with many particles significantly on a macroscopic level.

Gas is one of the four fundamental states of matter – the others being solid, liquid, and plasma.
The Nosé–Hoover thermostat is a deterministic algorithm for constant-temperature molecular dynamics simulations. It was originally developed by Nosé and was improved further by Hoover. Although the heat bath of Nosé–Hoover thermostat consists of only one imaginary particle, simulation systems achieve realistic constant-temperature condition. Therefore, the Nosé–Hoover thermostat has been commonly used as one of the most accurate and efficient methods for constant-temperature molecular dynamics simulations.
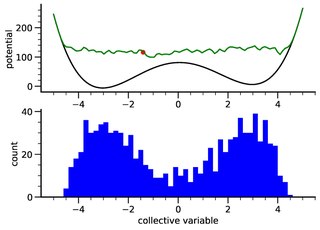
Metadynamics is a computer simulation method in computational physics, chemistry and biology. It is used to estimate the free energy and other state functions of a system, where ergodicity is hindered by the form of the system's energy landscape. It was first suggested by Alessandro Laio and Michele Parrinello in 2002 and is usually applied within molecular dynamics simulations. MTD closely resembles a number of recent methods such as adaptively biased molecular dynamics, adaptive reaction coordinate forces and local elevation umbrella sampling. More recently, both the original and well-tempered metadynamics were derived in the context of importance sampling and shown to be a special case of the adaptive biasing potential setting. MTD is related to the Wang–Landau sampling.

Michele Parrinello is an Italian physicist particularly known for his work in molecular dynamics. Parrinello and Roberto Car were awarded the Dirac Medal and the Sidney Fernbach Award in 2009 for their continuing development of the Car–Parrinello method, first proposed in their seminal 1985 paper, "Unified Approach for Molecular Dynamics and Density-Functional Theory". They have continued to receive awards for this breakthrough, most recently the Dreyfus Prize in the Chemical Sciences and the 2020 Benjamin Franklin Medal in Chemistry.
Physically based animation is an area of interest within computer graphics concerned with the simulation of physically plausible behaviors at interactive rates. Advances in physically based animation are often motivated by the need to include complex, physically inspired behaviors in video games, interactive simulations, and movies. Although off-line simulation methods exist to solve most all of the problems studied in physically-based animation, these methods are intended for applications that necessitate physical accuracy and slow, detailed computations. In contrast to methods common in offline simulation, techniques in physically based animation are concerned with physical plausibility, numerical stability, and visual appeal over physical accuracy. Physically based animation is often limited to loose approximations of physical behaviors because of the strict time constraints imposed by interactive applications. The target frame rate for interactive applications such as games and simulations is often 25-60 hertz, with only a small fraction of the time allotted to an individual frame remaining for physical simulation. Simplified models of physical behaviors are generally preferred if they are more efficient, easier to accelerate, or satisfy desirable mathematical properties. Fine details are not important when the overriding goal of a visualization is aesthetic appeal or the maintenance of player immersion since these details are often difficult for humans to notice or are otherwise impossible to distinguish at human scales.
The prediction of crystal properties by numerical simulation has become commonplace in the last 20 years as computers have grown more powerful and theoretical techniques more sophisticated. High accuracy prediction of elastic, electronic, transport and phase properties is possible with modern methods.
Qbox is an open-source software package for atomic-scale simulations of molecules, liquids and solids. It implements first principles molecular dynamics, a simulation method in which inter-atomic forces are derived from quantum mechanics. Qbox is released under a GNU General Public License (GPL) with documentation provided at http://qboxcode.org. It is available as a FreeBSD port.
References
- 1 2 Harvey, Stephen C.; Tan, Robert K.-Z.; Cheatham, Thomas E. (May 1998). "The flying ice cube: Velocity rescaling in molecular dynamics leads to violation of energy equipartition". Journal of Computational Chemistry. 19 (7): 726–740. doi:10.1002/(SICI)1096-987X(199805)19:7<726::AID-JCC4>3.0.CO;2-S.
- 1 2 3 4 Bussi, Giovanni; Donadio, Davide; Parrinello, Michele (2007-01-07). "Canonical sampling through velocity rescaling". The Journal of Chemical Physics. 126 (1): 014101. arXiv: 0803.4060 . Bibcode:2007JChPh.126a4101B. doi:10.1063/1.2408420. ISSN 0021-9606. PMID 17212484. S2CID 23411901.
- 1 2 Braun, E.; Moosavi, S. M.; Smit, B. (2018). "Anomalous Effects of Velocity Rescaling Algorithms: The Flying Ice Cube Effect Revisited". Journal of Chemical Theory and Computation. 14 (10): 5262–5272. arXiv: 1805.02295 . doi:10.1021/acs.jctc.8b00446. PMID 30075070. S2CID 51910357.