Berge's theorem

Last updated

In graph theory, Berge's theorem states that a matching M in a graph G is maximum (contains the largest possible number of edges) if and only if there is no augmenting path (a path that starts and ends on free (unmatched) vertices, and alternates between edges in and not in the matching) with M.

Contents

It was proven by French mathematician Claude Berge in 1957 (though already observed by Petersen in 1891 and Kőnig in 1931).

Proof

To prove Berge's theorem, we first need a lemma. Take a graph G and let M and M′ be two matchings in G. Let G′ be the resultant graph from taking the symmetric difference of M and M′; i.e. (M - M′) ∪ (M′ - M). G′ will consist of connected components that are one of the following:

  1. An isolated vertex.
  2. An even cycle whose edges alternate between M and M′.
  3. A path whose edges alternate between M and M′, with distinct endpoints.

The lemma can be proven by observing that each vertex in G′ can be incident to at most 2 edges: one from M and one from M′. Graphs where every vertex has degree less than or equal to 2 must consist of either isolated vertices, cycles, and paths. Furthermore, each path and cycle in G′ must alternate between M and M′. In order for a cycle to do this, it must have an equal number of edges from M and M′, and therefore be of even length.

Let us now prove the contrapositive of Berge's theorem: G has a matching larger than M if and only if G has an augmenting path. Clearly, an augmenting path P of G can be used to produce a matching M′ that is larger than M — just take M′ to be the symmetric difference of P and M (M′ contains exactly those edges of G that appear in exactly one of P and M). Hence, the reverse direction follows.

For the forward direction, let M′ be a matching in G larger than M. Consider D, the symmetric difference of M and M′. Observe that D consists of paths and even cycles (as observed by the earlier lemma). Since M′ is larger than M, D contains a component that has more edges from M′ than M. Such a component is a path in G that starts and ends with an edge from M′, so it is an augmenting path.

Corollaries

Corollary 1

Let M be a maximum matching and consider an alternating chain such that the edges in the path alternates between being and not being in M. If the alternating chain is a cycle or a path of even length, then a new maximum matching M′ can be found by interchanging the edges found in M and not in M. For example, if the alternating chain is (m1, n1, m2, n2, ...), where mi ∈ M and ni ∉ M, interchanging them would make all ni part of the new matching and make all mi not part of the matching.

Corollary 2

An edge is considered "free" if it belongs to a maximum matching but does not belong to all maximum matchings. An edge e is free if and only if, in an arbitrary maximum matching M, edge e belongs to an even alternating path starting at an unmatched vertex or to an alternating cycle. By the first corollary, if edge e is part of such an alternating chain, then a new maximum matching, M′, must exist and e would exist either in M or M′, and therefore be free. Conversely, if edge e is free, then e is in some maximum matching M but not in M′. Since e is not part of both M and M′, it must still exist after taking the symmetric difference of M and M′. The symmetric difference of M and M′ results in a graph consisting of isolated vertices, even alternating cycles, and alternating paths. Suppose to the contrary that e belongs to some odd-length path component. But then one of M and M′ must have one fewer edge than the other in this component, meaning that the component as a whole is an augmenting path with respect to that matching. By the original lemma, then, that matching (whether M or M′) cannot be a maximum matching, which contradicts the assumption that both M and M′ are maximum. So, since e cannot belong to any odd-length path component, it must either be in an alternating cycle or an even-length alternating path.

Related Research Articles

In mathematics, Hall's marriage theorem, proved by Philip Hall (1935), is a theorem with two equivalent formulations:

This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In the mathematical discipline of graph theory, a matching or independent edge set in an undirected graph is a set of edges without common vertices. Finding a matching in a bipartite graph can be treated as a network flow problem.

Perfect graph

In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the order of the largest clique of that subgraph. Equivalently stated in symbolic terms an arbitrary graph is perfect if and only if for all we have .

In graph theory, the perfect graph theorem of László Lovász states that an undirected graph is perfect if and only if its complement graph is also perfect. This result had been conjectured by Berge, and it is sometimes called the weak perfect graph theorem to distinguish it from the strong perfect graph theorem characterizing perfect graphs by their forbidden induced subgraphs.

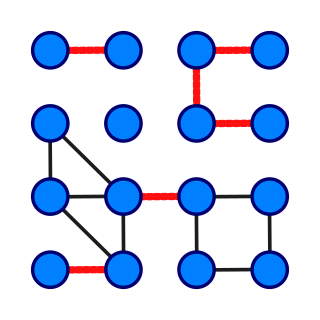
Bridge (graph theory) Edge in node-link graph whose removal would disconnect the graph

In graph theory, a bridge, isthmus, cut-edge, or cut arc is an edge of a graph whose deletion increases the graph's number of connected components. Equivalently, an edge is a bridge if and only if it is not contained in any cycle. For a connected graph, a bridge can uniquely determine a cut. A graph is said to be bridgeless or isthmus-free if it contains no bridges.

In the mathematical discipline of graph theory the Tutte theorem, named after William Thomas Tutte, is a characterization of graphs with perfect matchings. It is a generalization of Hall's marriage theorem from bipartite to arbitrary graphs. It is a special case of the Tutte–Berge formula.

In graph theory, the Dulmage–Mendelsohn decomposition is a partition of the vertices of a bipartite graph into subsets, with the property that two adjacent vertices belong to the same subset if and only if they are paired with each other in a perfect matching of the graph. It is named after A. L. Dulmage and Nathan Mendelsohn, who published it in 1958. A generalization to any graph is the Edmonds–Gallai decomposition, using the Blossom algorithm.

Kőnigs theorem (graph theory) Theorem showing that maximum matching and minimum vertex cover are equivalent for bipartite graphs

In the mathematical area of graph theory, Kőnig's theorem, proved by Dénes Kőnig (1931), describes an equivalence between the maximum matching problem and the minimum vertex cover problem in bipartite graphs. It was discovered independently, also in 1931, by Jenő Egerváry in the more general case of weighted graphs.

In computer science, the Hopcroft–Karp algorithm is an algorithm that takes as input a bipartite graph and produces as output a maximum cardinality matching – a set of as many edges as possible with the property that no two edges share an endpoint. It runs in time in the worst case, where is set of edges in the graph, is set of vertices of the graph, and it is assumed that . In the case of dense graphs the time bound becomes , and for sparse random graphs it runs in time with high probability.

Factor-critical graph

In graph theory, a mathematical discipline, a factor-critical graph is a graph with n vertices in which every subgraph of n − 1 vertices has a perfect matching.

Handshaking lemma Lemma that every node-link graph has an even number of odd-degree vertices

In graph theory, a branch of mathematics, the handshaking lemma is the statement that, in every finite undirected graph, the number of vertices that touch an odd number of edges is even. In more colloquial terms, in a party of people some of whom shake hands, the number of people who shake an odd number of other people's hands is even. The handshaking lemma is a consequence of the degree sum formula, also sometimes called the handshaking lemma, according to which the sum of the degrees equals twice the number of edges in the graph. Both results were proven by Leonhard Euler (1736) in his famous paper on the Seven Bridges of Königsberg that began the study of graph theory.

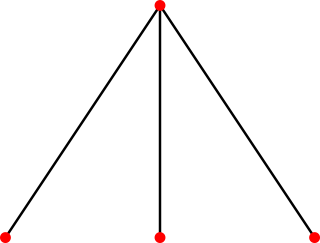
Claw-free graph

In graph theory, an area of mathematics, a claw-free graph is a graph that does not have a claw as an induced subgraph.

Tutte–Berge formula Characterization of the size of a maximum matching in a graph

In the mathematical discipline of graph theory the Tutte–Berge formula is a characterization of the size of a maximum matching in a graph. It is a generalization of Tutte theorem on perfect matchings, and is named after W. T. Tutte and Claude Berge.

In graph theory, a branch of mathematics, a skew-symmetric graph is a directed graph that is isomorphic to its own transpose graph, the graph formed by reversing all of its edges, under an isomorphism that is an involution without any fixed points. Skew-symmetric graphs are identical to the double covering graphs of bidirected graphs.

The blossom algorithm is an algorithm in graph theory for constructing maximum matchings on graphs. The algorithm was developed by Jack Edmonds in 1961, and published in 1965. Given a general graph G =, the algorithm finds a matching M such that each vertex in V is incident with at most one edge in M and |M| is maximized. The matching is constructed by iteratively improving an initial empty matching along augmenting paths in the graph. Unlike bipartite matching, the key new idea is that an odd-length cycle in the graph (blossom) is contracted to a single vertex, with the search continuing iteratively in the contracted graph.

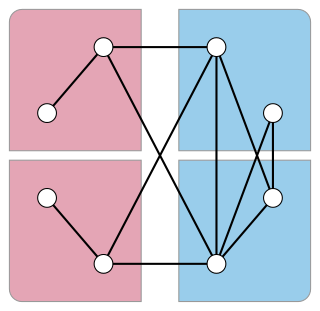
Skew partition

In graph theory, a skew partition of a graph is a partition of its vertices into two subsets, such that the induced subgraph formed by one of the two subsets is disconnected and the induced subgraph formed by the other subset is the complement of a disconnected graph. Skew partitions play an important role in the theory of perfect graphs.

Petersens theorem

In the mathematical discipline of graph theory, Petersen's theorem, named after Julius Petersen, is one of the earliest results in graph theory and can be stated as follows:

Petersen's Theorem. Every cubic, bridgeless graph contains a perfect matching.

In graph theory, a Hall violator is a set of vertices in a graph, that violate the condition to Hall's marriage theorem.

In graph theory, a balanced hypergraph is a hypergraph that has several properties analogous to that of a bipartite graph.

References

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.