
In mathematics, the gamma function is one of a number of extensions of the factorial function with its argument shifted down by 1, to real and complex numbers. Derived by Daniel Bernoulli, if n is a positive integer,
In mathematics, a power series is an infinite series of the form
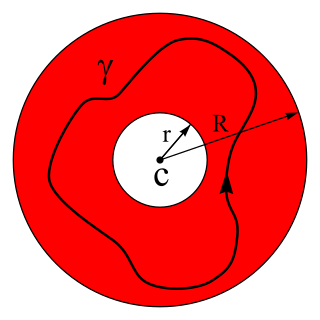
In mathematics, the Laurent series of a complex function f(z) is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where a Taylor series expansion cannot be applied. The Laurent series was named after and first published by Pierre Alphonse Laurent in 1843. Karl Weierstrass may have discovered it first in a paper written in 1841, but it was not published until after his death.

The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter gamma.
In mathematics, a generalized hypergeometric series is a power series in which the ratio of successive coefficients indexed by n is a rational function of n. The series, if convergent, defines a generalized hypergeometric function, which may then be defined over a wider domain of the argument by analytic continuation. The generalized hypergeometric series is sometimes just called the hypergeometric series, though this term also sometimes just refers to the Gaussian hypergeometric series. Generalized hypergeometric functions include the (Gaussian) hypergeometric function and the confluent hypergeometric function as special cases, which in turn have many particular special functions as special cases, such as elementary functions, Bessel functions, and the classical orthogonal polynomials.

In mathematics, the digamma function is defined as the logarithmic derivative of the gamma function:

In mathematics, the Hurwitz zeta function, named after Adolf Hurwitz, is one of the many zeta functions. It is formally defined for complex arguments s with Re(s) > 1 and q with Re(q) > 0 by
The Gram–Charlier A series, and the Edgeworth series are series that approximate a probability distribution in terms of its cumulants. The series are the same; but, the arrangement of terms differ. The key idea of these expansions is to write the characteristic function of the distribution whose probability density function f is to be approximated in terms of the characteristic function of a distribution with known and suitable properties, and to recover f through the inverse Fourier transform.

In mathematics, the exponential integral Ei is a special function on the complex plane. It is defined as one particular definite integral of the ratio between an exponential function and its argument.
In mathematics, a confluent hypergeometric function is a solution of a confluent hypergeometric equation, which is a degenerate form of a hypergeometric differential equation where two of the three regular singularities merge into an irregular singularity. There are several common standard forms of confluent hypergeometric functions:
In mathematics, the Gaussian or ordinary hypergeometric function2F1(a,b;c;z) is a special function represented by the hypergeometric series, that includes many other special functions as specific or limiting cases. It is a solution of a second-order linear ordinary differential equation (ODE). Every second-order linear ODE with three regular singular points can be transformed into this equation.
In mathematics, Riemann's differential equation, named after Bernhard Riemann, is a generalization of the hypergeometric differential equation, allowing the regular singular points (RSPs) to occur anywhere on the Riemann sphere, rather than merely at 0, 1, and . The equation is also known as the Papperitz equation.
In mathematics, basic hypergeometric series, or hypergeometric q-series, are q-analogue generalizations of generalized hypergeometric series, and are in turn generalized by elliptic hypergeometric series. A series xn is called hypergeometric if the ratio of successive terms xn+1/xn is a rational function of n. If the ratio of successive terms is a rational function of qn, then the series is called a basic hypergeometric series. The number q is called the base.
In 1893 Giuseppe Lauricella defined and studied four hypergeometric series FA, FB, FC, FD of three variables. They are :
In mathematics, in the area of combinatorics, a q-Pochhammer symbol, also called a q-shifted factorial, is a q-analog of the Pochhammer symbol. It is defined as

In probability theory and statistics, the Conway–Maxwell–Poisson distribution is a discrete probability distribution named after Richard W. Conway, William L. Maxwell, and Siméon Denis Poisson that generalizes the Poisson distribution by adding a parameter to model overdispersion and underdispersion. It is a member of the exponential family, has the Poisson distribution and geometric distribution as special cases and the Bernoulli distribution as a limiting case.
In mathematics, Maass wave forms or Maass forms are studied in the theory of automorphic forms. Maass wave forms are complex-valued smooth functions of the upper half plane, which transform in a similar way under the operation of a discrete subgroup of as modular forms. They are Eigenforms of the hyperbolic Laplace Operator defined on and satisfy certain growth conditions at the cusps of a fundamental domain of . In contrast to the modular forms the Maass wave forms need not be holomorphic. They were studied first by Hans Maass in 1949.
In mathematics, a Barnes integral or Mellin–Barnes integral is a contour integral involving a product of gamma functions. They were introduced by Ernest William Barnes. They are closely related to generalized hypergeometric series.

In probability theory and directional statistics, a wrapped Cauchy distribution is a wrapped probability distribution that results from the "wrapping" of the Cauchy distribution around the unit circle. The Cauchy distribution is sometimes known as a Lorentzian distribution, and the wrapped Cauchy distribution may sometimes be referred to as a wrapped Lorentzian distribution.
In mathematics, the Fox–Wright function is a generalisation of the generalised hypergeometric function pFq(z) based on ideas of Charles Fox (1928) and E. Maitland Wright (1935):

In computing, a Digital Object Identifier or DOI is a persistent identifier or handle used to uniquely identify objects, standardized by the International Organization for Standardization (ISO). An implementation of the Handle System, DOIs are in wide use mainly to identify academic, professional, and government information, such as journal articles, research reports and data sets, and official publications though they also have been used to identify other types of information resources, such as commercial videos.
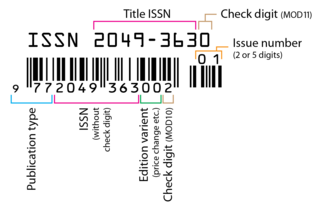
An International Standard Serial Number (ISSN) is an eight-digit serial number used to uniquely identify a serial publication, such as a magazine. The ISSN is especially helpful in distinguishing between serials with the same title. ISSN are used in ordering, cataloging, interlibrary loans, and other practices in connection with serial literature.
Mathematical Reviews is a journal published by the American Mathematical Society (AMS) that contains brief synopses, and in some cases evaluations, of many articles in mathematics, statistics, and theoretical computer science. The AMS also publishes an associated online bibliographic database called MathSciNet which contains an electronic version of Mathematical Reviews and additionally contains citation information for over 3.5 million items as of 2018.
















